What is the Length of a Year on Planet Sitnikov?
Posted February 2008.
The natural question is: How can one describe the motion? The answer is surprisingly complicated,...
Bill Casselman
University of British Columbia, Vancouver, Canada
cass at math.ubc.ca
In an impossibly distant galaxy far, far away lies the Sitnikov system, in which a single bizarre planet orbits a pair of stars. Well ... "orbit" isn't quite the word, as we shall see, although the planet certainly moves under the influence of the gravity due to the massive stars. In our solar system, the planets are far smaller than the sun, and their motion is not affected in a major way by each other - each of them moves in an orbit very close to the ellipse that it would describe if there were in fact no other planets in the system. Planets in a binary star system, where there are two suns of large mass instead of one, behave very differently. We'll take a look at one of the simplest possible examples, that first examined by the Soviet mathematician K. Sitnikov.
Binary star motion
The stars are assumed to have equal mass, and we assume their center of gravity to be at rest - in fact I'll take it to be the origin of our coordinate system. The stars therefore move in congruent ellipses with the origin as common focus.
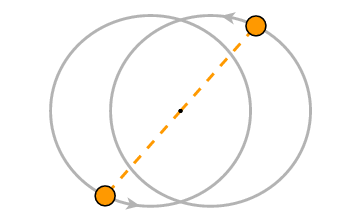
I'll allow the eccentricity e of the orbits to be arbitrary. If the major semi-axis of the orbit is a, the distance of the focus from the center of the ellipse is f = ae and the minor semi-axis b is a times the square root of 1-e2. The first changes linearly with e but the second only quadratically. This means that for small e the orbit will be fairly circular, but the effect of eccentricity on the motion will still be very noticeable. This is because Kepler's Second Law requires that the orbital motion sweep out equal areas in equal times. The star moves more rapidly when it is closer to the focus.
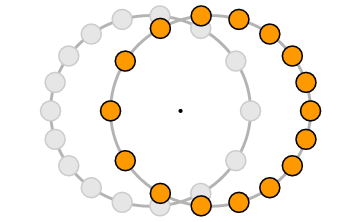
In this figure, e = 0.3.
The position of the stars is shown at equal time intervals.
Introducing the planet
We now place a very, very small planet into the system. It will 'orbit' in a rather peculiar manner - we assume that it simply moves along the line perpendicular to the plane of the stars, passing through the common focus of the stellar orbits. We shall look at what happens in the limiting case where the mass of the planet vanishes. The gravitational force on the planet varies for two reasons - for one thing, the planet moves back and forth away from the stellar plane, and on the other the stars themselves are moving. The force of gravity is greatest when the planet crosses the stellar plane and the stars are at periastron (nearest to the focus).

A very small planet moves perpendicularly to the motion of the stars.
The natural question is: How can one describe the motion? The answer is surprisingly complicated, and much of what happens is a good model for what happens in much more complicated situations.
The starting point is the differential equation expressing Newton's Law of Gravity. Choose units of mass, length, and time so that each star has mass 1/2, the period of stellar motion is 2π, and the gravitational constant is 1. With these assumptions, the motion of the small planet is governed by the second order differential equation
z'' = - z / (z2 + r2(t))3/2
where z is the height of the planet above the stellar plane, and r(t) is the distance from one of the stars to the focus of its orbit, which is calculated from Kepler's Second Law.
The case of circular motion
There is one situation which is far, far simpler than all others - when the eccentricity of the motion of the stars vanishes, or in other words when the stars move in a circle.

The only simple case is when the stars move in a circle.
In this case, the function r(t) is (again, because of our scaling of units) the constant 1/2, so the motion is described by the relatively simple differential equation
z'' = - z / (z2 + 1/4)3/2 .
in which there is no t-dependency. Multiplying this by z' and integrating, we see that the quantity
Ε = (z')2/2 - 1 / √ (z2 + 1/4)
remains constant. This is the limit of the expression for energy per unit mass as the mass of the planet tends to 0. That it remains constant is a form of the law of conservation of energy, which does not remain true in any useful way when r varies. This is a kind of paradox, but related to the fact that if the mass of the planet does not vanish then its motion affects that of the stars themselves - the law of conservation of energy applies only to the system as a whole.
The constant must lie at -2 or above. It is easy to see that the motion remains bounded if and only if Ε < 0. So as time goes on the point (z, z') must cycle around the curve Ε = C where -2 ≤ C < 0. These curves look like this:

The curves of constant energy.
Here z is the horizontal axis, z' the vertical one.
The blue area marks the bounded trajectories.
When the motion in this simple case is bounded, the planet just keeps cycling through a given family of states. This motion amounts to an oscillation back and forth across the stellar plane. Since the restoring force of gravity weakens with distance from equilibrium, the period of oscillation is larger for larger swings. This is opposed to what happens for a harmonic oscillator, where the period is independent of the amplitude.
The following figure exhibits the graphs of z versus time t. In each case, at time t=0 the planet starts with velocity 0 at a specified height.

Here e = 0.
Plots of z versus t for three initial conditions (with eccentricity e=0).
In summary, the case where e=0 is quite understandable, even reasonably predictable, albeit only with some work involved in actually predicting motion. The work becomes somewhat less sophisticated if one uses integral formulas due to mathematicians of the early 20th century expressing the motion in terms of elliptic integrals. This idea goes back to Euler.
When eccentricity does not vanish
When e > 0 things are much more interesting. We can get some idea of what happens by looking at the analogues of the graphs plotted above in a particular example. The following two graphs plot the motion for the same initial conditions as earlier, and at the same scale, but now for e = 0.1 and e=0.2.

z versus t for e = 0.1.
Here, with e=0.1, the graphs for the two low values of initial height (in red and orange) are reasonably well-behaved - almost periodic, one might say - but the third graph looks rather wild. It does not, in fact, seem possible to say exactly what is going on.

z versus t for e = 0.2.
The same impression of chaotic behavior remains even more valid for e=0.2. The first two graphs are again close to being periodic. But the chaos implicit in the third is even more pronounced. This becomes even clearer if we look at the continuations of the first of these graphs for further values of t:
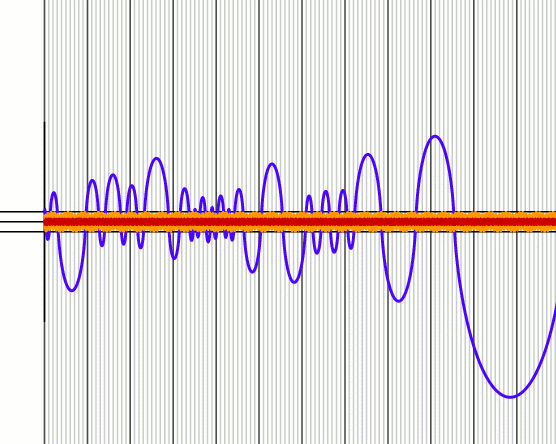
z versus t for e = 0.1 (wider range of t-values)
It looks very much as if the planet were about to escape to infinity, or at the very least oscillate with increasing and unbounded magnitude as time goes on. This kind of behavior can be intuitively explained in terms of a 'sling shot' effect, similar to what happens when a comet's orbit in our solar system is seriously modified when it passes close to Jupiter.
In fact, just about anything is possible. The basic theorem in the subject is essentially due to Sitnikov and Alekseev. It is proven carefully and with reasonable clarity in Moser's book. Suppose we associate to every planet trajectory a sequence (sk) of integers - we record the number of integral stellar periods between every two successive crossings of the stellar plane by the planet, both forward and backward in time.
For any given value of e > 0 there exists an integer m with the property that any sequence (sk) with all sk ≥ m will be associated to some planet trajectory in the system with eccentricity e.
This theorem allows coming from or escaping to infinity, in which case the sequence stops at one end or the other. Moser's proof introduces structures much like Smale's famous horseshoe, where a similar theorem is proven about sequences of bits.
Sections of motion
One way to visualize what is going on is to take snapshots of the planet in various situations. In Moser's book, he does this by recording, as we have already seen, when the planet crosses the stellar plane. Another way to do this is by recording position and velocity at regular time intervals. The natural choice is the period of the stars. In the first figure below, this is done for the case e=0. In this case the curves traced are the level curves of energy, which we have already seen.
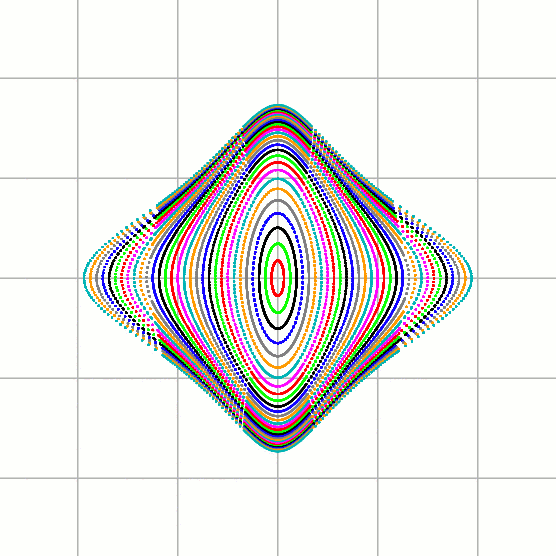
Plots of (z, z') at moments t = 2πn, with e=0.
In the next two pictures we see the plots for e=0.1 and e=0.2. The potential chaos now shows up in that the successive points plotted no longer lie on a continuous curve.
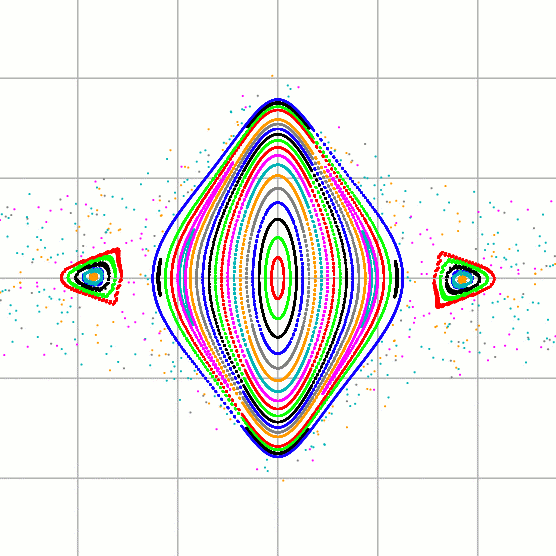
Plots of (z, z') at moments t = 2πn, with e=0.1.
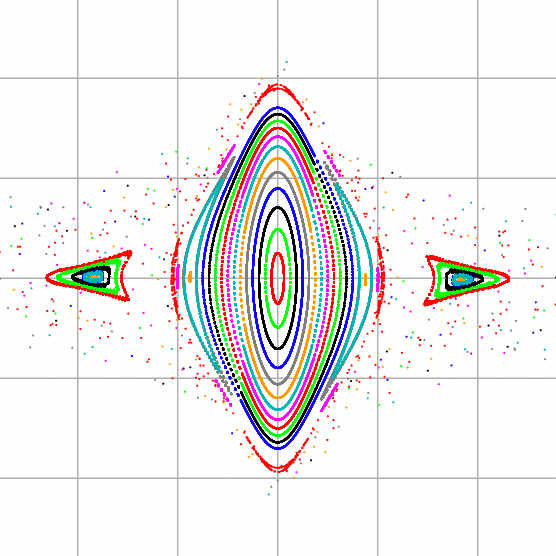
Plots of (z, z') at moments t = 2πn, with e=0.2.
Explaining exactly what's going on is rather complicated. One thing that is not so complicated, however, is explaining the 'islands' one sees, say in the second plot. One of the islands is centered at (z, z') = (1.847, 0). If I plot the solution of the differential equation with those initial conditions, I get:

Graph of z versus t with initial conditions (1.847, 0).
This is very, very close to a periodic solution that is in a 1:2 resonance with the stellar motion - 1 oscillation of the planet every 2 stellar periods. Other `islands' barely visible in the plots correspond to other resonances. Resonance is a basic pattern in dynamical systems.
How the plotting was carried out
Solutions to the differential equations describing the planet's motion were computed by a variant of the extrapolation method of Bulirsch-Stoer described in the well-known book Numerical Recipes.
To find out more
The literature on Sitnikov's system is very large, but in spite of that I am not aware of any single account of Sitnikov's system that is at once easily readable, thorough, and reliable. Accounts that attempt to be rigorous are not always clear, and those that attempt to give an intuitive explanation of what's going on rarely make any attempt at all to prove claims.
- Numerical Recipes, published by Cambridge Press in endless editions. The home page for the book is http://www.nr.com/. Selections are available without payment, but with some mild if annoying restriction on usage.
- R, Dvorak, F. Freistetter, and J. Furths, Chaos and stability in planetary systems, Springer, 2004. Section 6 of Part I is a fairly readable account of the Sitnikov system, although marred by sloppiness. As far as I can tell, for example, at least one of the differential equations whose solutions they calculate is not actually one attached to a physically realistic situation - in effect they seem to have forgotten that the gravitational force attracting the planet to the stars is the same as that attracting the stars towards each other. Still, their discussion is useful and suggestive. The section on Sitnikov's system is available in toto through Google Books.
- J. Moser, Stable and random motions in dynamical systems, Princeton University Press, 1973. This is the classic reference about the Sitnikov system, with rigorous and complete proofs. It is a tough read, but a significant improvement on the expositions of his predecessors.
- K. Sitnikov, The existence of oscillatory motions in the three-body problems, Doklady Akademii Nauk SSSR (Physics), 133 (1960), 303-306. This is essentially the origin of the subject, in which complicated oscillating solutions were first found. in modern times.
- Carles Simó, Dynamical systems, numerical experiments, and super-computing, preprint available form Simó's web site. This helps make Moser's arguments more concrete.
Bill Casselman
University of British Columbia, Vancouver, Canada
cass at math.ubc.ca
Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet can be used to get additional bibliographic information and reviews of some these materials. Some of the items above can be accessed via the ACM Portal , which also provides bibliographic services.


















