Mathematics and Sports
Posted April 2010.
Some of the fascinating mathematics of sports scheduling...
Joseph Malkevitch
York College (CUNY)
malkevitch at york.cuny.edu
Introduction
Sports in America is both big business and democracy in action. Baseball, football, and basketball have become writ large, with games on television and cable television generating huge sums of money that goes into the American economy. But sports are also a mechanism whereby American children learn the values of fair play, hard effort, and the meaning of friendship.
Mathematics Awareness Month was created to help focus the public's attention on the nature of mathematics and the way it affects our daily lives and fosters the development of new tools to solve problems for individuals, businesses, and governments. This year the theme for Mathematics Awareness Month is Mathematics and Sports.
The first areas where people think about mathematics being applied are in the sciences and engineering. Yet mathematics plays a large role in the efficiency of sports. Coaches constantly try to find ways to get the most out of their athletes, and sometimes they turn to mathematics for help. This help may include the best batting order for a team to maximize the number of runs it can score or the putting together of a program for an Olympic skater so that the jumps the skater makes take advantage of the scoring bonus when these jumps are performed later in a program when tiredness starts to set in. There are also mathematical issues involved in scoring systems for some of the complex and subjective aspects of scoring sports events.
However, the sheer magnitude of the number of games that must be played in league sports creates a large domain for mathematics to assist in the efficient operation of sports. This runs the gamut from "intellectual" sports such as bridge, whist, and chess, to sports such as baseball, football, basketball, soccer, and cricket. Here I will limit myself to some of the fascinating mathematics of sports scheduling and some related fairness and optimization questions that use relatively elementary or quick starting methods.
One way of getting insight into a complex environment is to classify what one sees and study the objects in each of the categories separately as a way of simplifying things. In fact there are many types of tournaments:
* round robin tournament (each team plays exactly k games against every other team (player))
Note: Very often the value of k = 1 is so each team or player gets to play exactly one game (match) against every other team or player.
* elimination tournament (the tournament progresses n rounds where in each round some players are eliminated and the surviving players are paired in future rounds, where again losers are eliminated)
Note: there are variants of this, especially double elimination tournaments. In this idea losers in the various rounds of elimination play against each other and, thus, a later series of victories can lead to a final victory.
* king of the hill (a player stays on the court for as long as he/she can beat the next challenger)
Perhaps the very first question that arises in scheduling is to design the matches that must occur for a round robin tournament. In a single round robin tournament (SRRT) each team must play exactly one game against every other team. We will devote what follows mostly to single round robin tournaments. Many questions arise where mathematics provides insight. First, there is the issue of scheduling. If there are 8 teams, what is an efficient way to schedule the matches that must take place? Another question, about which there is a huge literature but which will not be treated here, is how to decide on the winner based on the results or scores that the players attain. For example, if one has 8 teams, could the number of wins of the eight teams in decreasing order be 6, 5, 5, 4, 4, 2, 2, 0? Questions about rankings for teams in tournaments are closely related to the issues of ranking candidates in an election or ranking choices for economic policy.
Graph theory helps schedule tournaments
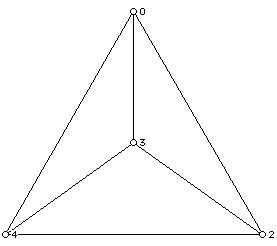
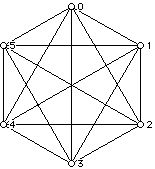
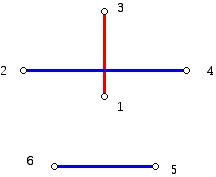
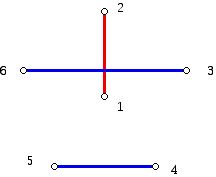
Graph theory, a branch of combinatorics which draws heavily on geometrical ideas, uses diagrams consisting of dots and lines to help get insight into a variety of mathematical problems. The complete graph on n vertices has exactly one edge between every pair of vertices. These graphs are denoted Kn; Figure 1 shows K4 and Figure 2 shows K5.
Figure 1
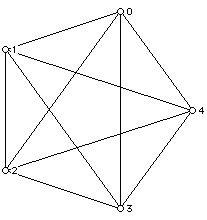
Figure 2
In each case the vertices of the graph are labeled with the names of the people or teams involved in the "tournament" or competition. Think of the vertices (dots) of a complete graph as representing the teams in a tournament and think of an edge joining two teams as being a match played by those two teams. The number of edges of the complete graph with n vertices is n(n-1)/2, which is the number of matches that must be carried out in order to have each team play every other team exactly once. Note that in the graph Kn each vertex has n-1 edges at each vertex. The number of edges at a vertex of a graph is known as its degree or valence.
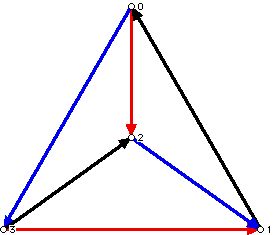
Consider first the case where there are 4 teams that must play each other. This means a total of 4(3)/2 = 6 matches must be played. These matches could be played in 6 time slots, say one a week for 6 weeks. However, it might be desirable if venues (rooms; playing fields) for the matches are available to have several matches per time slot and the games be completed over a shorter period of time. Thus, since there are 4 players, and 4/2 is 2, we could consider having two matches per time slot, and complete the tournament in three weeks rather than 6 weeks. When I use the phase "time slot," there are various possibilities as to how the matches are actually played. Note that two matches per time slot might mean that there would be two games at exactly the same time or that the games be played in the morning and afternoon on the same "court" of a single day. There are a variety of terms used other than time slots, and a common one is "rounds," which I will use interchangeably with time slots and Event Window. Figure 3 shows the details of how the scheduling could work.
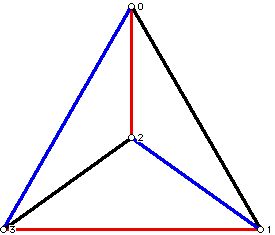
Figure 3
Edges in the graph that have the same color would occur during one time slot. Thus, for Event Window 1 (shown in blue) there would be matches between team 0 and team 3 and team 1 and team 2; for Event Window 2 (shown in black) we would pair team 0 and team 1 and team 2 and team 3; and for Event Window 3 (shown in red) we would pair team 0 and team 2 and team 1 and team 3.
In attempting to use the ideas above we come to a complication when we try to extend what we have done from 4 teams to 5 teams. Since 5 is an odd number we can not merely have all the teams play in pairs during an Event Window. There is a natural way to handle this problem. The concept of a "bye" in sports scheduling refers to a team's not having to play a match (game) during a particular Event Window. If one has 5 teams, there are 10 matches (games) that must be carried out for a round robin tournament where each team plays every other. Since 5/2 is not an integer, we can not play 3 games per Event Window but we can play 2 games per Event Window (4 teams play) and assign a bye to one team. Thus, in five Event Windows we can schedule the whole tournament. You can see the way a schedule for the five Event Windows can be constructed and see the team which has a bye in each Event Window by consulting Figure 4.
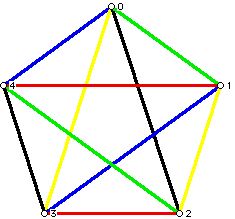
Figure 4
The edges in different colors signify which teams play in an Event Window. For example, the two yellow edges tell one can have teams 0 and 3 and 1 and 2 play each other in a single Event Window; for that event window team 4 would get a bye. The other pairings for each Event Window can be similarly handled. Note that there is considerable flexibility in the arrangement of the colors into the five Event Windows.
If a collection of edges are disjoint from each other it is called a matching. If a graph G has a matching M which includes all of the vertices of the graph, then M is said to be a perfect matching. A necessary condition for a perfect matching is that the number of vertices of the graph be even. K4 has a perfect matching while K5 does not. However, it is not difficult to find examples, such as the one in Figure 5, which has an even number of vertices, every vertex of valence 3 (e.g. 3 edges at a vertex), but for which there is no perfect matching.
Figure 5
A pioneer in using graph theory as a tool for solving scheduling problems has been Dominique De Werra, who has spent much of his career at the Polytechnic University of Lausanne.

During that time he has made a variety of contributions to sports scheduling and operations research in general. Many of the basic results were described during the 1980's by De Werra. Interest in this subject has grown so large that there is now an online discussion group devoted to sports scheduling issues from both practical and theoretical viewpoints.
Another name for a perfect matching is a 1-factor. A k-factor one is a subgraph of the graph which includes all the vertices of the graph and where each vertex in the subgraph has the valence (degree) k. So when a graph has a 1-factor, we can think of the vertices as teams and the edges as games which the vertices (teams) joined by an edge play against each other. Returning to our sports scheduling situation, when we have a complete graph which has an even number of vertices, we can ask if it has a collection of 1-factors which include all of the edges of the graph. The coloring we found for K4 in Figure 3 shows that this graph has a 1-factorization into three 1-factors. Because of the special way we drew K4 it may not be clear that we can continue to find 1-factorizations of complete graphs with even numbers of vertices. To see the different in suggestiveness of different drawings, look at this drawing of K4 (Figure 6).
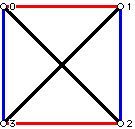
Figure 6
In this version we can see that the edges of different colors can be interpreted as being in "parallel classes." Even though the edges 02 and 13, which are black, appear to meet, they meet at a point which is not a vertex so we will think of this drawing as having three parallel classes. One can, in fact, interpret this diagram as a finite affine plane with 4 points. Every line of the plane has two points on it. There are six lines and 3 lines through every point.
Now we move up to round robin tournaments with 6 teams (Figure 7). Fifteen matches are to be played. Since there are 6 players this means having 3 games per Event Window for 15/3 = 5 Event Windows.
Figure 7
In light of what happened for four teams it is tempting to take a boundary edge 01 in Figure 7 of the regular hexagon shown, and construct a matching by using the edges that do not meet this edge (that are parallel to it, as it were). If we do this we get the games: 01, 25, and 34. Proceeding around the boundary we get another two groups of matches: 12, 03, 45, and 23, 14, 05. This seems to take us off to a good start. There are 6 edges remaining so our hope is to group these into two sets of size 3. However, unfortunately the six edges that remain form two disjoint triangles: edges 02, 24, 04 and 13, 15, 35. Now since we can not pick two disjoint edges from either of these triangles we reach a dead end. There is no way we can take our initial group of teams for the first three time windows and extend the result to two more time windows! Although mathematicians love to reason by analogy and try to apply simple principles to solve a problem at hand, sometimes the analogy may not hold up, as we see in this case.
However, we will not lose heart. Perhaps we can try some alternate systematic way to schedule 6 teams in a round robin tournament. Here is a method that works and generalizes. Here we number the teams from 1 to n rather than from 0 to n-1. We will consider only the case with an even number of teams, since when there is an odd number of teams, as already explained we can add a fictional team and whenever a real team is asked to play the fictional team, the real team has a bye.
Consider the case with 6 teams. Construct an initial table with the first half of the teams listed consecutively in the first row and the last half of the teams listed in reverse order in the next row. The teams that line up in the table will play in the first round.
Round 1:
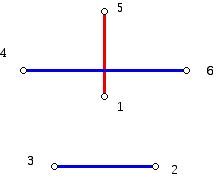
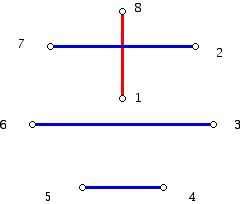
We can use the graph below to visualize what is going on. The edge 1 to 6 is shown vertically in a diagram where the vertex 1 is placed at the "center" of a regular pentagon and the numbers 2 and 3 are listed clockwise starting from 1, while the numbers 5 and 4 are shown counterclockwise starting at 6. In the diagram shown the edges which make up the sides of the regular convex pentagon are omitted. Only the edges which make up the pairings in one round for the teams are shown. The other edges of the matching (in addition to the pairing of 1 and 6, shown in red) are shown horizontally in blue. (Two colors are used to highlight the different role of the vertical and horizontal edges in the diagram. However, in the partition of the complete graph on 6 vertices into 3 disjoint edges, these three edges would be in one color class.) Since there are 5 rounds each with 3 edges we can account for all of the 15 edges in the complete graph on 6 vertices.
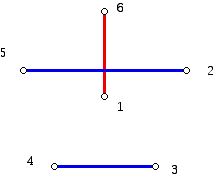
Figure 8
To get to the pairings for the next round we will fix the first team in the cell in the first row and first column but think of all the other teams as being in a necklace on a piece of string listed in the clockwise direction: 2, 3, 4, 5, and 6. Now rotate the necklace one position clockwise and record the entries into a new table: 6, 2, 3, 4, 5. We were thinking of 2 as being at the top of the clock, so after the rotation the last entry in the list is now at the top of the clock.
Round 2:
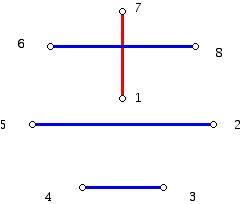
Here is an analogue of the diagram above after the rotation of the vertices in the regular pentagon:
Figure 9
We repeat this rotation operation until we exhaust the new pairings and return to the start.
Round 3:
with a corresponding labeled graph:
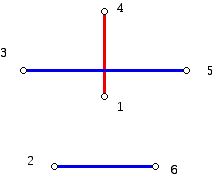
Figure 10
Round 4:
Figure 11
Round 5:
Figure 12
Another rotation would bring us back to where we started, so we are done.
Here are the first few founds of the schedule for 8 teams. Can you find the teams that play in the remaining rounds?
Round 1:
and a graph-theoretical way to see what is going on:
Figure 13
Round 2:
One additional sample of the rotation in the visual graph theory environment:
Figure 14
Round 3:
etc.
Earlier we pointed out the problem of an odd number of teams. The way out was to use a bye in each Event Window. Is there a way to use the elegant system above to unify the odd versus even case treatment? Mathematicians like the idea of taking an elegant way of handling something to deal with a related but "annoying" situation. The way to do this in the current situation is to always work with an even number of teams or players, even when the actual number of players is odd. When we have an odd number of players, we will always think of player number 1 as a "fictional" or nonexistent team. Now, whenever a player is assigned the fictional player 1 as an opponent, that real player is given a bye. Since, for example, in the pairings for 6 teams with the real players 2 to 6, in the diagrams above the red pairings with the fictional team 1 appear exactly once in the order 6, 5, 4, 3, 2. Thus, player 4 has a bye in the third round.
A common concern of mathematics is seeing things to be the same or equivalent when considered from some point of view. For example, the fractions 3/6 and 1/2 certainly look different but they can be used interchangeably in calculations which involve fractions because they are "equivalent" rational numbers. One might wonder if the patterns of scheduling tournaments that are derived from 1-factorizations of complete graphs are equivalent or different. Not surprisingly, if one has two teams there is only one way to schedule a tournament between them. What about 4-player tournaments such as we constructed a schedule for based on the edge colorings of the complete graph on 4 vertices in Figure 1? There we named the players 0 to 3 but in the "rotation" procedure shown above we used the names 1 to 4 for the players. Clearly, renaming of the players does not change a schedule. However, one might be interested in how many essentially different ways there are of scheduling 2n teams. First done by hand and then continuing with computers this question is being attacked. It is tempting to be lulled into "complacency" by the slow start of this sequence: for two players there is 1 schedule, for 4 players and 6 players 1 schedule, and for 8 players only 6 are possible. However, things take off from here as shown by the sequence of values starting at n = 2 (n even):
1, 1, 1, 6, 396, 526915620, 1132835421602062347
This shows that one can try to achieve some other goals by selecting schedules that might have other "desirable" properties beyond the easy way of describing the construction that we have indicated above.
Extensions and generalizations
One natural pragmatic concern for scheduling tournaments is where the games are played. For some tournaments the games may be played on "neutral" territory where the opponents are not at some advantage because of being on their home field or having the encouragement of the hometown fans. However, in a lot of sports there is this issue of home and away games. Is there some easy way to take this issue into account?
The diagram below (Figure 15) shows a copy of the 3 matchings of K4 where each edge has been assigned an orientation, that is, an arrow head has been placed on each edge. I will use the "standard convention" from the scheduling literature that a directed edge from i to j will mean that for the match between i and j, the game will be a home game for j. Using H for home and A for away, the schedule shown with the arrows gives rise to this pattern of rounds with away and home games indicated:
Round 1 (Red matching): 0 (away) plays 2 (home); 1 (home) plays 3 (away)
Round 2 (Black matching): 0 (away) plays 1 (home); 2 (home) plays 3 (away)
Round 3 (Blue matching): 0 (home) plays 3 (away); 1 (home ) plays 2 (away).
One can record this information in a somewhat different way. For each player, list in the three rounds whether its games are home or away.
Team 0: A (Red), A (Black), H (Blue)
Team 1: H (Red), H (Black), H (Blue)
Team 2: H (Red), H (Black), A (Blue)
Team 3: A (Red), A (Black), A (Blue)
This does not seem quite fair because team 1 plays all three of its games at home while team 3 plays all three of its games away. However, since there are 4 teams and 6 matches we can not equalize the number of home and away games for each team. Put differently, since there are three rounds, in each round the number of home and away games can not be equal for any team!
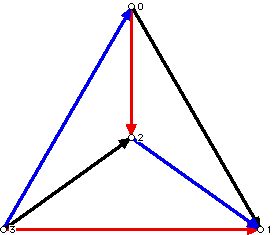
Figure 15
Could one at least find a schedule where the number of home and away games differ in absolute value by 1?
The answer is that for a four-player tournament such a schedule is possible.
Figure 16
Round 1 (Red matching): 0 (away) plays 2 (home); 1 (home) plays 3 (away)
Round 2 (Black matching): 0 (home) plays 1 (away); 2 (home) plays 3 (away)
Round 3 (Blue matching): 0 (away) plays 3 (home); 1 (home ) plays 2 (away).
and in terms of the patterns for each team:
Team 0: A (Red), H (Black), A (Blue)
Team 1: H (Red), A (Black), H (Blue)
Team 2: H (Red), H (Black), A (Blue)
Team 3: A (Red), A (Black), H (Blue)
In considering the pattern of home and away games one might want to have home and away games alternate for each team or, from a different point of view all the home and away games be in a consecutive block. When it might be possible, one might also want to have equal numbers of home and away games. Now, for situations with an even number of teams since the degree (number of edges at a vertex) of a vertex in the complete graph is odd, we can not have equal numbers of home and away games. For complete graphs with an odd number of vertices we can ask for the even number of games each team plays to be equally divided between home and away games, but we have to recall that in each round there will exactly one bye if all the other teams play in that round.
What are the tools that mathematics has brought to bear on these scheduling questions? In the graph theory realm the methods involve finding 1-factorizations of complete graphs, as well as other ways to partition (organize the edges into disjoint subsets) the edges of complete graphs. Sometimes one can a find a 2-factor (a subgraph where each edge has degree (valence) 2) and a 1-factor which together account for all the edges of a complete graph. For example, in Figure 3 if one takes the union of the edges with any two different colors, we get a 2-factor of the graph, and edges of the third color form a 1-factor. In fact, this idea can be used to get the appealing way to orient the edges of the complete graph on four vertices shown in Figure 16. If we orient the edges of the 2-factor to form a "directed cycle," then we can orient the remaining two edges to get a home-away pattern that is symmetrical for a tournament with 4 teams. (This pattern does not have totally equal treatment for the four teams, but if there is a schedule of games for the fall and another for the spring the roles of the teams can be interchanged and fairness restored over the longer period.)
Mathematics has responded to the need for finding "good" schedules in the most commonly required settings with a variety of ideas. If, in light of the discussion above, one limits oneself to scheduling an even number n of teams (players), then one can carry out two phases, in an attempt at producing a "nice" schedule:
Phase I
Schedule n/2 matches for each of the n-1 rounds (Event Windows).
What is produced by this phase is determining for each team which opponent it will have in each of the rounds.
Phase II
For each of the matches scheduled in Phase I between pairs of players (teams) one decides which of the two teams in the match plays at home and which team plays away.
For the "opponent schedule" produced in phase I, phase II produces a "home-away assignment."
In some situations the issue of home/away does not matter but it usually does. Thus, for each team, one can produce a sequence of n-1 H's and A's which represent the home/away pattern of games that team must play.
For example, for the opponent schedule generated from Figure 16 we have for Team 0 the sequence AHA and for Team 3 the sequence AAH. It is commonly viewed that consecutive games at home or away are undesirable. In the scheduling literature two such consecutive home or away games is called a break. It turns out to be a classical insight from mathematical analysis that any home-away assignment for an "opponent schedule" can not be done with fewer than n-2 breaks.
The proof of this fact is rather appealing, so here goes. First, no two teams can have identical home-away patterns because if they did, they would not get to play each other, which is required in a round robin tournament! So we can have at most one home-away sequence where home and away alternate and which starts and ends with home, and at most one such home away sequence that starts and ends with away. Thus, we must have at least n-2 teams which have at least one break!
The opponent schedule given in Figure 3 and the home-away schedule derived from this opponent schedule as in Figure 16 has exactly 4-2 =2 breaks, and, thus, achieves the minimum. If one is given an opponent schedule S one can let Bminimum denote the minimum number of breaks taking into account all ways of assigning home and away patterns to the paired teams in S. It is known (Dominique de Werra showed this) that one can (for even n) find an opponent schedules where Bminimum is n-2. It has also been shown that for a given opponent schedule one can decide whether or not it can be given a home-away assignment (that is, one can carry out Phase II, above) that achieves n-2 breaks in polynomial time. Yet, given an arbitrary S the computational complexity of finding the value of Bminimum is unclear. It may require exponential time to carry out this calculation.
Our discussion has given some clues to the many ways that graph theory can be used to get insights into scheduling problems for different sports. Another area of mathematics that has also very fruitful for this purpose is the theory of block designs. Many web sites now offer the opportunity to print out tournament arrangements for various numbers of teams.
When you sit down to watch your favorite sports star or team I hope you will recognize the behind-the-scenes role that mathematics is playing in bringing these events to you and making it possible to have fair, competitive and efficient sports events. If you are a "little league" mom or dad or participant, perhaps you can enjoy the mathematics behind the sports, as well as the sport itself.
Support Mathematics Awareness Month!
References:
Anderson, I., Constructing tournament designs, Mathematical Gazette, 73 (1989) 284-292.
Anderson, I., Combinatorial Designs, Ellis Horwood, Chichester, 1990.
Anderson, I. (1999) Balancing carry over effects in tournaments, in Combinatorial designs and their applications, Chapman & Hall/CRC Res. Notes Math., 403, Boca Raton, FL, 1-16.
Anderson, I. and N. Finizio, Cyclic white tournaments, Discrete Mathematics, 125 (1994) 5-10.
Briskorn, D., Sport leagues scheduling: models, combinatorial properties, and optimization algorithms, Ph.D. thesis, 2007, Christian-Albrechts-Universität Kiel, Lecture Notes in Economics and Mathematical Systems, Vol. 603.
Briskorn, D., Combinatorial properties of strength groups in round robin tournaments, European Journal of Operational Research 192 (2009) 744-754.
Briskorn, D., Sports League Scheduling, Vol., 603, Lecture Notes in Economics and Mathematical Systems, Springer, New York, 2008.
Briskorn, D. and S Knust, Constructing fair sports league schedules with regard to strength groups, Discrete Applied Mathematics 158 (2010) 123-135.
Brouwer, A. and G. Post, G. Woeginger, Tight bounds for break minimization in tournament scheduling, Journal of Combinatorial Theory A, 115 (2008) 1065-1058.
Colbourn, C. and J. Dinitz, J. (eds.), Handbook of Combinatorial Designs, 2nd edition, CRC Press, 2006.
Della Croce, F. and R. Tadei, P. Asioli, Scheduling a round robin tennis tournament under courts and players availability constraints, Annals of Operations Research, 92 (1999) 349-361.
de Werra, D., Geography, games, and graphs, Discrete Applied Mathematics 2, (1980) 327-337.
de Werra, D., Scheduling in sports, Annals of Discrete Mathematics, 11 (1981) 381-395.
de Werra, Minimizing irregularities in sports scheduling using graph theory, Discrete Applied Mathematics, 4 (1982) 217-226.
de Werra, D., Some models of graphs for scheduling sports competitions, Discrete Applied Math., 21 (1988) 47-65.
de Werra, D. and T Ekim, C. Raess, Construction of sports schedules with multiple venues, Discrete Applied Math., 154 (2006) 47-58.
de Werra, D. and L. Jacot-Descombes, P. Masson, A constrained sports scheduling problem, Discrete Applied Mathematics 26 (1980) 41-49.
K. Easton, G. Nemhauser, and M. Trick, Sport Scheduling, in J.Y.-T. Leung, (ed.), Handbook of Scheduling: Algorithms, Models, and Performance Analysis, Chapman and Hall/CRC, 2004, pp. 52-8 to 52-9.
Elf, M. and M. Junger, G. Rinaldi, Minimizing breaks by maximizing cuts, Operations Research Letters, 31 (2003) 343-349.
Geinoz, A. and T. Ekim, D. de Werra, Construction of balanced sports schedules using partitions into subleagues, Operations Research Letters, 36 (2008) 279-282.
Glenn, W., A comparison of the effectiveness of tournaments, Biometrika, 47 (1960) 253-262.
Harary, F. and L. Moser, The theory of round robin tournaments, Amer. Math. Monthly, 73 (1966) 231-246.
Haselgrove, J. and J. Leech, A tournament design problem, Amer. Math. Monthly, 84 (1977) 198-201.
Healey, P., Construction of balanced doubles schedules, Journal of Combinatorial Theory A, 29 (1980) 280-286.
Henz, M., Scheduling a major college basketball conference, Oper. Research, 46 (1998) 1-6.
Kendall, G. and S. Knust, C. Ribeiro, S. Urrutia, Scheduling in sports: An annotated bibliography, Computers & Operations Research, 37 (2010) 1-19.
Knust, S., Scheduling sports tournaments on a single court minimizing waiting times, Operations Research Letters, 36 (2008) 471-476.
Mather, J. and M. Smith, S. Jowett, K. Gibson, Application of photogrammetric technique to golf club evaluation, Journal of Sports Engineering, 3 (2000) 249.
Mendelsohn, E. and A. Rosa, On some properties of 1-factorizations of complete graphs, Congr. Numer., 24 (1979) 43-65.
Mendelsohn, E. and A. Rosa, One factorizations of the complete graph: A survey, J. of Graph Theory, 9 (1985) 43-65.
Miyashiro R. and T. Matsui, A polynomial time algorithm to find an equitable home-away assignment, Operations Research Letters, 33 (2005) 235-241.
Moon, J., Topics on Tournaments, Holt, Rinehart, Winston, New York, 1968.
Nabieyev, V. and H. Pehlivan, Applied Mathematics and Computation, 1999 (2008) 211-22.
Nemhauser, G. and M. Trick, Scheduling a major college basketball conference, Operations Research, 46 (1998) 1-8.
Post, G. and G. Woeginger, Sports tournaments, home-away assignments, and the break minimization problem, Discrete Optimization, 3 (2006) 165-173.
Rasmussen, R. and M. Trick, Round Robin Scheduling - a survey, European J. of Operations Research, 188 (2008) 617-636.
Rosa, A. and W. Wallis, Premature sets of 1-factors or how not to schedule round-robin tournaments, Discrete Applied Mathematics, 4 (1982) 291-297.
Russell, R. and J. Leung, Devising a cost effective schedule for a baseball league, Operations Research 42 (1994) 614-625.
Scheid, F., A tournament problem, Amer. Math. Monthly, 67 (1960) 39-41.
Schreuder, J., Combinatorial aspects of construction of competition Dutch professional football leagues, Discrete Applied Mathematics, 33 (1992) 301-312.
Smith, M. and J. Mather, K.. Gibson, S. Jowett, Measuring the dynamic response of a golf club during swing and impact, Photogrammetric Record, 16 (1998), 249-257.
Trick, M. A schedule-then-break approach to sports timetabling, in Proceedings of the 3rd Conference on Practice and Theory of Automated Timetabling, PATAT' 2001, Lecture Notes in Computer Science, Volume 2079, Springer, Berlin, 2001, pp. 242-253.
Urban, T. and R. Russell, Scheduling sports competitions on multiple venues, European J. Oper. Res., 148 (2003) 302-311.
Wallis, W., One-factorizations of graphs: Tournament applications, College Math. J., 18 (1987) 116-123.
Wallis, W., One-factorizations of complete graphs, In Contemporary Design Theory, Wiley, 1992, pp. 692-731.
Wallis, W., One factorizations, Kluwer, Dortrecht, 1997.
Weert, A. and J. Schrender, Construction of basic match schedules for sports competitions using graph theory, in Lecture Notes in CS, Volume 1408, Springer, Berlin, 1998, pp. 201-210.
Joseph Malkevitch
York College (CUNY)
malkevitch at york.cuny.edu
Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet can be used to get additional bibliographic information and reviews of some these materials. Some of the items above can be accessed via the ACM Portal , which also provides bibliographic services.