Fourier Analysis of Ocean Tides II Feature Column Archive
2. Almost orthogonality
We work under the hypothesis that the tidal record at any port, written as a function of time, is a combination of sines and cosines of the form A0 + A1cos(v1t) + B1sin(v1t) + A2cos(v2t) + B2sin(v2t) + ... where the ``speeds'' v1, v2, ... are part of a finite collection of possible speeds, determined globally by astronomical considerations. Since we can expect no rational relation between the astronomical constants, the tidal record will not be periodic. But this special structure will allow us to determine the coefficients A0, A1, B1, A2, B2, ... directly from the tidal record, by adapting the Fourier analysis of periodic functions to this non-periodic one.
Sample problem.
Let us start with a simple non-periodic function like f(t) = 2sin(t) - 3sin(21/2t).
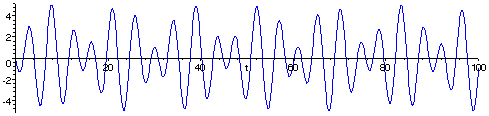
The graph of f(t) = 2sin(t) - 3sin(21/2t). Because 21/2 is not rational, this function can never repeat itself exactly. Suppose that we know that the function is of the form f(t) = B1sin(t) + B2sin(21/2t), and are given the curve. How to calculate the coefficients B1 and B2?
Tools from trigonometry.
- any product of sines can be rewritten as a difference of cosines. Specifically,
sin(v1t)sin(v2t) = .5cos([v1-v2]t) - .5cos([v1+v2]t).
- the long-term average value of cos(vt), for any non-zero v, is zero.
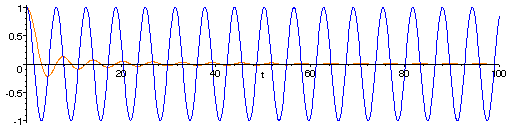
The graphs of cos(t) (blue) and of the average value of the cosine function from 0 to t (yellow).
- It follows that the long-term average of sin(v1t)sin(v2t) is zero unless v1 = v2 or v1 = -v2. We can mimic the language of ordinary Fourier series and say that under these conditions the two functions sin(v1t) and sin(v2t) are almost orthogonal.
- the long-term average value of sin2(vt) is 1/2, for any non-zero speed v.
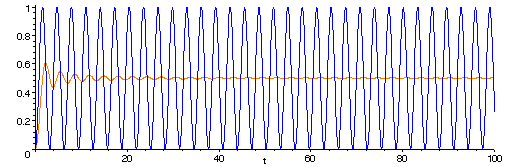
The graphs of sin2(t) (blue) and of the average value of the sine-squared function from 0 to t (yellow).
The solution.
To calculate B1: multiply f(t) by sin(t) and compute twice the long-term average value of the product. This number must be B1. Why? The product is
f(t)sin(t) = B1sin2(vt) + B2sin(t)sin(21/2t).
The average value is the sum of the average values of the two terms. The first has average value B1/2 while the second has long-term avarage value zero. To calculate B2: multiply f(t) by sin(21/2t) and compute twice the long-term average value of the product. This number must be B2.
The following graph shows how the multiplications and long-term averaging tease out the coefficients B1 = 2 and B2 = -3.
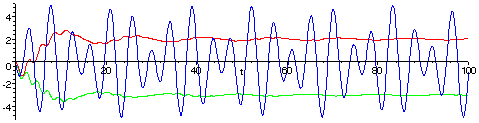
The graph of f(t) is plotted in blue, the running average of 2f(t)sin(t) is plotted in red, and the running average of 2f(t)sin(21/2t) is plotted in green.
Welcome to the
Feature Column!
These web essays are designed for those who have already discovered the joys of mathematics as well as for those who may be uncomfortable with mathematics.
Read more . . .
Feature Column at a glance






