A Non-Commutative Marriage System in the South Pacific
Posted October 2009.
The Ambrym system has at its heart a fundamentally non-trivial mathematical object: a non-commutative group...
Tony Phillips
Stony Brook University
tony at math.sunysb.edu
Introduction
The social structure of isolated indigenous populations has given anthropologists a useful quantitative tool for studying how people have evolved and dispersed. These structures often incorporate general abstract principles, but the precise way these principles are worked out can vary enormously from society to society. Marriage patterns are especially complicated and especially stable. An analogy from the natural world is the organization of the flowering parts (the reproductive organs) of plants. The variety is enormous, but because the structure is integral to the way one generation produces the next, it tends to be very stable in time; its analysis is an essential part of the study of species and their relatedness.
The island populations of the South Pacific, and in particular the the inhabitants of Ambrym (part of the Vanuatu archipelago, roughly 1500 miles northeast of Australia), have received sustained attention in this respect since the late 19th century. Ambrym is prominent in Lévi-Strauss' Les Structures Élémentaires de la Parenté (The Elementary Structures of Kinship) (1947) and is the subject of a recent study (Knut Mikjel Rio, The Power of Perspective: Social Ontology and Agency on Ambrym Island, Vanuatu, Berghahn Books, New York, 2007), which is the basis for my analysis in this column.
One aspect of the marriage system on Ambrym that anthropologists have noted, besides its intricacy, is the lucidity with which the people themselves explain its workings. Bernard Deacon (1927) observed: "It is perfectly clear that the natives (the intelligent ones) do conceive of the system as a connected mechanism which they can explain by diagrams. The way they could reason about relationships from their diagrams was absolutely on a par with a good scientific exposition in a lecture-room." So it is especially satisfying to note that the Ambrym system has at its heart a fundamentally non-trivial mathematical object: a non-commutative group.
The male perspective
The following diagram is adapted from Rio's Figure 3.1.
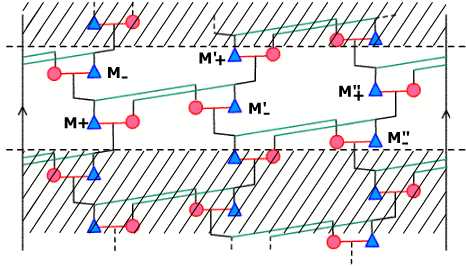
Blue triangles, males; red circles, females. This cylindrical diagram shows the division of Ambrym society into three patrilineal lines, and the possible marriage relationships between them, in the style of a genealogical tree. The three male lines are marked here as M, M' and M''. In each of these lines there is an alternation between generations: those who marry "right" (+) and those who marry "left" (-) in this diagram. Thus an M'+ chooses a wife among the sisters of M''- individuals, whereas an M'- marries a sister of of an M+.
Note that there is a more genealogical distinction between the "+" and the "-" generations. A member of a "+" generation marries into a slightly older generation, while a member of a "-" generation marries into one slightly younger. In fact, the father of the father of the father of an individual is of his great-grandfather's generation; but tracing through the diagram shows that the father-in-law of the father-in-law of the father-in-law of an M+ (for example) is of his great-great-grandfather's generation, whereas the triple father-in-law of an M- is only of his grandfather's generation.
Implicit in this diagram is a non-commutative group with 6 elements, generated by the kinships S : father --> son and T : father --> son-in-law. First observe that S2 = I, where I is the identity kinship relating each of the six classes to itself. This is because the grandson of an M- is again an M-, etc. Next, T3 = I : for example, the son-in-law of an M- has married the sister of an M+, hence is an M'-, as above; similarly the son-in-law of an M'- must be an M''- and the the son-in-law of an M''- must be an M-, so after three steps we are back where we started. An additional consequence of Rio's diagram is the less obvious equation T2 = STS. For example, the son-in-law of the son-in-law of an M- is an M''-, as we just saw; and the son of the son-in-law of the son of an M- is the son of the son-in-law of an M+, i.e. the son of an M''+ (see the diagram), and is also an M''-.
The equations S2 = I, T3 = I and T2 = STS are the same as those that govern the group of symmetries of a triangle.
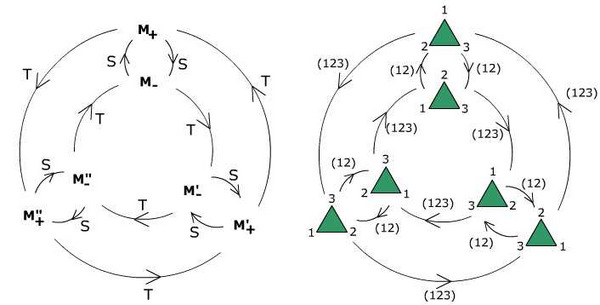
The marriage-kinship structure of Ambrym society is isomorphic to the group S3 of symmetries of an equilateral triangle. Each symmetry corresponds to a permutation of the vertices, labeled here as 1, 2, 3. Matching the "son" kinship S with the permutation (12) [flip about the axis through vertex 3] and the "son-in-law" kinship T with the permutation (123) [counterclockwise rotation by 120o] extends to a complete identification of the two systems. The diagram on the left is in fact quite similar to that drawn in the sand by Deacon's native informant in 1927 (Rio, p. 49).
The group S3 is the simplest example of a non-commutative group. The operation of composition (execute permutation p, then permutation q) has all the formal properties of addition of integers (associativity, identity element, inverses) except the commutative property, the one that guarantees that 2 + 3 = 3 + 2. Thus, it need not be the case that executing the permutation p followed by q results in the same permutation as executing q followed by p. The Ambrym kinship group has the same structure. For example ST is not the same as TS : the son of the son-in-law of an M+ is an M''-, whereas his son-in-law's son is an M'-.
The female perspective
Rio's diagram can be redrawn to show the female lineages.
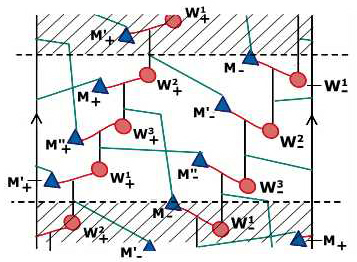
Ambrym society has two female lineages, here labeled W+ and W-, and in each lineage there are functionally three generation-classes, here distinguished by 1, 2, 3. The "+" lineage only marries males from the "+" generations; the "-" lineage only marries males from the "-" generations. The kinships D : mother --> daughter and E : mother --> daughter-in-law satisfy D3 = I, E2 = I and D2 = EDE, generating another copy of S3. Observe a complication in the diagram: the generations W1+, W2+, W3+ pair with M'+, M+, M''+ respectively, whereas W1-, W2-, W3- pair with M-, M'-, M''- respectively (different order).
The "male perspective" is more biological because there are six male genotype clusters (Y-chromosome, mitochondria) which follow the S, T permutation rules. The female lineages preserve mitochondria, but their generations cannot be distinguished genetically. Finally, Rio's diagram shows that the Ambrym system is efficient for genetic mixing: On the female side, each individual gets "+" chromosomes from the paternal grandmother and "-" chromosomes from the mother, or vice-versa; whereas after three generations the three male genotypes are equally represented in each individual.
Ambrym and the French intelligentsia ...
The publication of Deacon's diagram in Les Structures Élémentaires de la Parenté prompted a lively exchange between Lévi-Strauss and Jean-Paul Sartre, two of the high priests of the Parisian post-war mandarinate. The controversy is recorded mostly in Sartre's 1960 Critique de la raison dialectique ("To be born is to produce oneself as a specification of the group," etc.) and Lévi-Strauss' 1962 La Pensée Sauvage. Rio gives a careful analysis of their positions in a section entitled "Sartre and Lévi-Strauss meet the Man from Ambryn."
... including André Weil
In a completely different direction, Lévi-Strauss enlisted none other than André Weil in the mathematical elucidation of kinship structures; Weil contributed an eight-page appendix "Sur l'étude algébrique de certains types de lois de mariage (Système Murngin)" to the first part of Les Structures. It is enlightening to apply his algebraic analysis to the marriage system on Ambrym.
Weil understood the essence of a marriage-kinship system to be incorporated in a set of permitted marriage-types, satisfying the following axioms:
- (A) Every member of society, male or female, fits in exactly one permitted marriage-type.
- (B) For each member of society, the designated marriage-type is a function only of that individual's sex and the marriage-type of that individual's parents.
So the marriage-kinship system can be condensed into two functions, f and g in Weil's notation, giving the marriage-type of a male child and a female child, respectively, as a function of the marriage-type of that child's parents. Weil remarks that these functions must map the set of marriage-types onto itself, since otherwise certain types would disappear after two generations; and that therefore f and g are permutations of the set of marriage-types.
Applying Weil's analysis to Ambrym, we find six marriage-types:
- A = (M+, W2+)
- B = (M-, W1-)
- C = (M'+, W1+)
- D = (M'-, W2-)
- E = (M''+, W3+)
- F = (M''-, W3-).
These and the permutations f and g can be read off from the "Female Perspective" table above.
|
type
|
A |
B |
C |
D |
E |
F |
| f |
B |
A |
D |
C |
F |
E |
| g |
E |
D |
A |
F |
C |
B |
Since f includes the father --> son kinship, it is functionally equivalent to our operator T; and since one's daughter and son-in-law share the same marriage-type, g includes our operator S. In the same way g includes the mother --> daughter kinship, and f includes mother --> daughter-in-law, so they are also functionally equivalent to our E and D, respectively. In Weil's more efficient notation, the equations f 2 = I, g 3 = I, g 2 = f g f (which can readily be checked from the table above) contain both our (S, T) and (D, E) identities.
Unfortunately for us, the system Weil analyzed (the Murngin inhabit the northern tip of Australia) is mathematically less interesting than that of Ambrym. In the Murngin marriage code, the only sanctioned marriages are within a special class of "cross cousins:" between a man and one of his mother's brothers' daughters (equivalently, a woman and one of her father's sisters' sons). Weil encodes this as an additional axiom:
- (C) A man must be able to marry the daughter of the brother of his mother.
and then proves that Axiom C forces the group generated by f and g to be commutative. His proof runs as follows. Consider a brother and a sister, the product of marriage-type X. The brother will contract an f (X) type marriage, and his daughter will contract a g(f (X)) type marriage; the sister will contract a g(X) type marriage, and her son will contract one of type f (g(X)) . By axiom (C) this son must be able to marry his mother's brother's daughter; so these two young people must be of the same marriage-type, i.e. f (g(X))= g(f (X)) .
The rest of "Sur l'étude algébrique ..." only examines commutative systems.
Tony Phillips
Stony Brook University
tony at math.sunysb.edu
Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet can be used to get additional bibliographic information and reviews of some these materials. Some of the items above can be accessed via the ACM Portal , which also provides bibliographic services.








