The Mathematics of the Rainbow, Part II
I'll first recall in some detail the steps leading to Airy's formula for the intensity of light in a rainbow, and then say something about how Airy made it possible to compare his theory to experiment...
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
Email Bill Casselman
Introduction
A rough explanation of rainbows was given by Descartes in the early seventeenth century, but it did not account for all phenomena seen in them, notably the pale pink or green `supernumerary' arcs one sees below the main bow in this picture:

This photograph is cropped from Double-alaskan-rainbow.jpg, available from the Wikipedia Commons.
It is distributed under the Creative Commons Share-Alike license.
The explanation of these arcs requires the wave theory of light, and a reasonably accurate account was first put forth by the British mathematician George Biddell Airy around 1838. An earlier Feature Column discussed the elements of Airy's theory, but left much undone. This sequel will say more. I'll first recall in some detail the steps leading to Airy's formula for the intensity of light in a rainbow, and then say something about how Airy made it possible to compare his theory to experiment.
From light rays to wave fronts
The following pictures summarize the basic idea of Airy's argument.

|
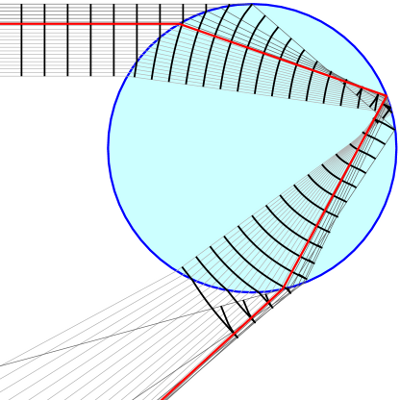
In Descartes' theory, the rays of the sun hit a spherical raindrop, reflect once inside it, and pass back out to an observer. Snell's law of refraction (plagiarized, probably, by Descartes) asserts that upon entering and exiting the drop, the rays bend. We now understand this to be because light travels more slowly in water.
But because of the geometry of the drop, the rays, although striking the drop uniformly, bunch up on exit, leading to an infinite intensity in one direction. The speed of light in water depends on the color of the light, and different colors bunch up in different directions. This leads to the ordinary rainbow seen most often.
From now on, I assume that the light striking the raindrops is monochromatic - that is to say, all of one color. This might seem unrealistic, but in fact all experimental work with rainbows reproduces this condition in order to make experimental data comprehensible. This has been true ever since W. H. Miller first tried to verify Airy's mathematics in the laboratory. With this assumption, the rays all bunch up along one particular ray, which was called by Airy the `caustic ray' because in other examples of a similar phenomenon, such as focusing of light by a lens, the concentration of light could burn.
|
|
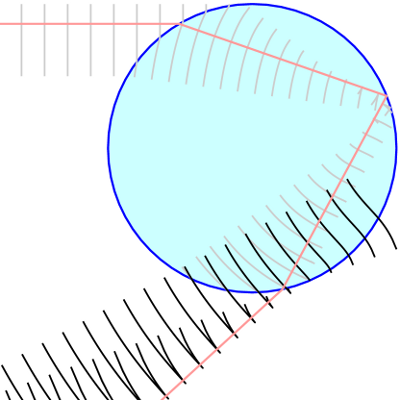
According to the wave theory of light, it propagates as waves. A surface on which the phase of a wave is constant is called a wave front. The distance between successive fronts of, say, phase $0$ is called the wavelength. Parts of the wave front of sunlight hit a raindrop at different times, so different parts of the wave front begin to slow down at different times. This leads to a curvature in the wave fronts.
|
 |
The caustic ray marks an extreme of the directions in which the rays go. On exiting, rays entering the raindrop above the caustic ray cross those entering from below it.
What is important in this picture is the way the wave front doubles back on itself, in effect mingling two waves, each with a different front. These two components of the waves mix with each other in a complicated fashion, leading to interference (and those bands of light I am trying to explain). In order to understand what's going on in simple terms, I'll use a trick - not looking at the true wavefront as it emerges from the drop, but looking instead at an effective or virtual wave front, which is the wave front in clear air that would cause the emerged wave front.
It is the crossing of the rays that causes the interference effects that bring about the supernumerary arcs, since it means the wave fronts also cross each other---the phases of the rays entering above the caustic ray are not constant on the wave fronts from those entering below. This means that the two sets of waves will sometimes supplement each other and sometimes cancel each other out.
|
Comments?
From wave fronts to Airy's formula
A moving wave front determines the light intensity according to `Huyghen's principle,' which says that each infinitesimal segment of the front behaves independently of other segments, and as a point source of light. In our case, we are looking at a series of wave fronts like this:

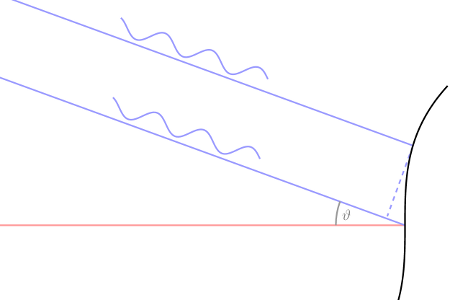
Looking at the rainbow, the observer is very, very far away. Therefore what we wish to know is how the intensity of light varies with the angle $\vartheta$ from the caustic ray. Each of the effective wave fronts will produce the same effect for the observer, but one of them, that at the far right, is by far the simplest to work with. If I choose a rotated coordinate system, it has an equation which may be approximated well enough near the $x$ axis by $$ y = -c x^{3} \quad(c > 0) \, . $$

The light waves hitting an observer at angle $\vartheta$ from the caustic ray will be the sum of contributions from all the rays on this cubic wave front. Contributions from different parts of this front will have different phases.
How can we calculate the total contribution?
|
Let $\delta_{x}$ be the difference in the length of paths from the observer to the origin and to the point $(x, y)$ on the wave front. The length of these paths is very large and $\delta_{x}$ is very small, comparable to the diameter of the raindrop. But it is still very large compared to the wavelength of light.
Suppose the amplitude of the light wave along the wave front to be $A\sin 2\pi ft$ ($f$ is the frequency) The amplitude of the light wave with wavelength $\lambda$ coming from $(x, y)$, at distance $\ell_{x}$ from the wave front, is $$ A(x) \sin 2\pi\Big(ft - { \ell_{x} \over \lambda }\Big) \, , $$ where $A_{x}$ is the amplitude on the wave front at position $x$. But $\ell_{x} = \ell_{0} - \delta_{x}$, so the total amplitude is $$ \eqalign { &= \int_{-W}^{W} A(x) \sin \Big( 2\pi\Big(ft - { \ell_{0} \over \lambda }\Big) + 2\pi \Big({\delta_{x} \over \lambda} \Big)\Big) \, dx \cr &= \sin 2\pi\Big(ft - { \ell_{0} \over \lambda }\Big) \int_{-W}^{W} A(x) \cos 2\pi \Big({\delta_{x} \over \lambda} \Big) \, dx + \cos 2\pi\Big(ft - { \ell_{0} \over \lambda }\Big) \int_{-W}^{W} A(x) \sin 2\pi \Big({\delta_{x} \over \lambda} \Big) \, dx \, . \cr } $$ Because the wavelength of light is so small compared to the diameter of the rain drop, we can make a number of simplifications. The basic point is that only the part of the integral for $x$ matters. This means that $A(x)$ may be assumed to be constant, that $\delta_{-x} = -\delta_{x}$, and that $W$ may be taken to be infinity. Furthermore, $\sin$ is an odd function. Therefore, since $\cos$ is an even function, the integral is $$ 2 A \sin 2\pi\Big(ft - { \ell_{0} \over \lambda }\Big) \int_{0}^{\infty} \cos 2\pi \Big({\delta_{x} \over \lambda} \Big) \, dx \, . $$
|

|
|
It remains to find a formula for $\delta_{x}$. From the figure at the right, we see that $$ \delta_{x} = x \sin \vartheta + y \cos \vartheta \, , $$
giving as the amplitude some constant times $$ \int_{0}^{\infty} \cos 2\pi \Big({-cx^{3} \cos \vartheta + x \sin \vartheta \over \lambda} \Big) \, dx \, . $$ Since we are looking at the rays near the caustic ray, $\vartheta$ is small. We may approximate $\cos \vartheta$ by $1$ and $\sin \vartheta$ by $\vartheta$. We get as approximation $$ \int_{0}^{\infty} \cos 2\pi \Big({cx^{3} - x \vartheta \over \lambda} \Big) \, dx \, . $$
|

|
A change of variables in the integral makes this $$ \hbox{constant} \cdot \int_{0}^{\infty} \cos {\pi\over 2} \, ( s^{3} - z s) \, ds \, . $$ This is
Airy's integral formula for the amplitude of a light wave near near the caustic ray of a rainbow. In this formula, $z$ is proportional to the angular distance $\vartheta$ from the caustic ray. The constant $C$ and the ratio $\vartheta/m$ depend on a number of things I have been careless about - the wavelength of the color involved, the size of the raindrop, and the intensity of sunlight. There have been a number of approximations applied, too - primarily that the only important contributions to the integral come from small values of $s$ in this integral, which I needed in order to replace $W$ by $\infty$. This should become clearer in the next section - the rough idea is that when $|s|$ is large the function $\cos(s^{3} - zs)$ oscillates very rapidly, and positive and negative oscillations cancel out. That fairly small values of $x$ in the original integral correspond to large values of $s$ is because the diameter of a rain drop is much, much larger than the wavelength of light. Other approximations are justified by the fact that the distance from the raindrop to the observer is much larger than the diameter of the rain drop. Such intuitive approximations are at the heart of physics.
Comments?
Airy's first try at computation
At any rate, once Airy's formula is at hand, we are faced with a purely mathematical problem: of what use is the formula?
The function $$ Ai(z) = \int_{0}^{\infty} \cos {\pi\over 2} \, ( x^{3} - z x) \, dx $$ is called (what else?) the Airy function. After Airy obtained his formula, he was faced with the problem of actually comparing what it told him with the phenomena actiually observed in rainbows. This required that he compute a range of values. This was not a trivial task, since the integral is over an infinite range, and we want to see what the function looks like over a wide range of values of $m$.
Let's begin by looking at the function $\cos (\pi/2) (x^{3} - zx)$ being integrated. It behaves quite differently for $m$ positive and negative. Here are some sample graphs:
In both cases, the graph oscillates more and more rapidly as $x \rightarrow \infty$. This explains why, at least, the infinite integral makes sense - it may be expressed as an infinite sum of terms decreasing in absolute value and alternating in sign, like the commonly seen sum $$ 1 - 1/2 + 1/3 - 1/4 + 1/5 - \cdots $$
But the graphs start out very differently for negative and positive values of $z$. The negative case is ... well, more interesting.
In his first paper, Airy computed a table of values of $Ai(z)$ for $z$ in the range $[-4,4]$. How did he do this? Why didn't he compute for a wider range?
The short answer to the first question is, in the most straightforward way possible. That is to say, the method he used did not rely on the very special function he was looking at, but instead could have been used on any function with behaviour generally similar to that of $Ai(z)$. Airy was not an imaginative man, but he was persistent. Dogged, you might say. Sometimes doggedness is more valuable than imagination, but as Airy demonstrated later on in his life, sometimes it is an impediment.
His table covers $41$ values of $z$ in the range $[-4,4]$. For each of these he computed $Ai(z)$ according to the same process. He first computed the finite integral $$ \int_{0}^{2} \cos (w^{3} - zw) \, dw $$ by a standard numerical method, approximating the integrand by a polynomial of degree $4$. His method seems somewhat more accurate than Simpson's rule. This step, as he points out, involved computing all in all $5,166$ values of the function $\cos (\pi/2) (w^{3} - zw)$! (Tables of $\cos(\theta)$, compiled by the French astronomer Delambre, were used. He does not say how many hours this took, but it cannot have been short work.)
The next step was to compute the integrals $$ \int_{2}^{\infty} \cos (\pi/2)(w^{3} - zw) \, dw \, . $$ For this, he used a method I have not seen anywhere else, an application of integration by parts. This gives him a series that does not converge, but which if treated with respect gives a good approximation. (Stokes was later to use a similar method more systematically.) Having followed so far and seen some distance into Airy's soul, you will not be too surprised to learn that his series were very complicated. One of them, for example, starts off $$ \eqalign { - { 8685956800 \over \pi^{8} } & \cdot { w \over (3w^{2} - m)^{12} } + { 450644705280 \, z \over \pi^{8} } \cdot { w \over (3w^{2} - m)^{13} } \cr & - { 717352796160 \, z^{2} \over \pi^{8} } \cdot { w \over (3w^{2} - m)^{14} } + { 358676398060 \, m^{3} \over \pi^{8} } \cdot { w \over (3w^{2} - m)^{15} } - \cdots } $$ with the value $w = 2$.
All in all, a remarkable effort and a convincing demonstration of the validity of the wave theory of light.
To interpret this illustration, keep in mind that light intensity is proportional to the square of amplitude.
I have said that $Ai(z)$ looks very different for positive and negative values of $z$. For $z < 0$, it decreases monotonically at an exponential rate, whereas for $z > 0$ it oscillates in with slowly decreasing amplitude. (I am not aware that Airy ever even conjectured that this might be so. Later in the century, Stokes founded a major branch of applied mathematics by proving these assertions.)
And then?
Airy's derivation of his formula was perhaps the highlight of his career as a physicist. His methods of computation, and perhaps his qualities as a mathematician, did not shine so brightly. Roughly about the time he did his calculations the mathematician De Morgan suggested a far more efficient technique involving relatively simple converging power series. But De Morgan's explanation was apparently not sufficiently justified in Airy's view to make him switch steeds in mid-stream. Many years later De Morgan did manage to convince Airy of the validity of his idea, and Airy wrote a supplement to his original paper including De Morgan's justification and applying his method. Here, too, however, there was a limit to how far Airy could calculate with these series. It was George Gabriel Stokes, one of the most brilliant mathematical physicists of he nineteenth century, who saw the way out of an apparent impasse. But that is another story.
Comments?
Reading further
-
G. B. Airy, `On the intensity of light in the neighbourhood of a caustic', in Volume VI of the Transactions of the Cambridge Philosophical Society (1838).
In the main part of this paper, Airy derives his integral formula with the help of a few rather obscure diagrams. In an Appendix he describes in exhaustive (and exhausting) detail his method for calculating $Ai(z)$. His main result is a table of values for $z$ in the range $[-4,4]$.
-
Airy (again), `Supplement to a paper on the intensity of light in the neighbourhood of a caustic', in Volume VIII of the Transactions of the Cambridge Philosophical Society (1848).
This is Airy's second run at computation. It incorporates an idea of Augustus De Morgan, whichj enables Airy to use a converging power series to compute $A(z)$. But it, too, runs into trouble. This, too, is part of another story.
-
Bill Casselman, The mathematics of rainbows
-
Anne O'Donnell, The work of G. G. Stokes in evaluating the Airy rainbow integral and its ramifications today
An ideal master's thesis. This is concerned with Stokes's considerable contributions to the calculation of Airy's integral.
-
W. H. Miller, `On spurious rainbows', in Volume VII of the Transactions of the Cambridge Philosophical Society (1841).
This is an account of looking for the supernumerary bows in laboratory conditions. Sunlight was passed through a narrow slit onto a cylinder of running water, then examined through a telescope fitted with a red filter. Several were seen, with varying degrees of distinctness.
-
R. A. R. Tricker, Introduction to meteorological optics, American Elsevier, 1970.
As I have written elsewhere, Tricker has written a number of books that are too sophisticated for idiots and too elementary for geniuses. All of them are worth reading. They offer a unique view of interesting aspects of science at an intermediate level. This one is perhaps his best, but the one on water waves is also readable and instructive.
I have been very vague on a number of points, and two of the most serious are that I describe a two-dimensional theory and that I ignore the polarized nature of light. Tricker briefly deals with each.
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
Email Bill Casselman


 Bill Casselman
Bill Casselman














