18" by 24" print, 2011. This image is a snap-shot from a real-time interactive particle simulation using Lorentz's Law to define each particle's movements. The color palette, perspective, magnetic field placement, and rendering style were designed by the artist. Physics and mathematics define the piece's motion and overall pattern formation. --- Reza Ali

11" x 11" x 4.5", Knitted cotton (Reynolds Saucy), 2010. I am a mathematician who knits as well as a knitter who does mathematics. It has always seemed natural to me to combine mathematics and knitting, and it is inevitable that sometimes the results will be artistic rather than functional. The Heawood bound shows that $K_7$ is the largest complete graph that can embed on the torus. This is an embedding of $K_7$ on the torus with all vertices centered on the largest longitude. It is the second knitted instantiation of this embedding; this version is larger and has a larger face-to-edge proportion than the first, which was exhibited at Gathering for Gardner 7 in 2006. --- sarah-marie belcastro

1276 x 1800 pixels, computer graphics, 2011. I use 2D and 3D computer graphics as well as photographs made by myself or my friends, to show the beauty of these objects, thus uniting the intellectual wonder of perceiving a mathematical concept with the aesthetical pleasure of viewing a beautiful image. Hanging gardens of Babylon were built in the desert as a wonder of land amelioration and engineering. In our era humanity continues to perform such wonders, e.g. in desert Australia. While the flowers on my picture, which have grown on the Möbius strip over the Australian plain, were placed there by computer graphics, it is the hard work of those who make the Red Continent green that invokes our admiration. Photographs of Australian views and the Florida festival in Canberra were used in this image. --- Tatiana Bonch-Osmolovskaya

6" x 6" x 2", Nylon (selective laser sintering), 2011. The mathematician in me is fascinated with the various roles that constraints play in optimization problems: sometimes they make problems much harder to solve; other times, much easier. Equivalent is a three-piece, 3D-printed sculpture that consists of three topologically equivalent variations of the Borromean rings. In the Borromean rings, no two of the three rings are linked, so if any one of them is destroyed, the remaining two rings will come apart. For the photograph, we positioned Equivalent on a piece of Lenox china (a wedding gift). --- Robert Bosch

20" x 20", Digital print, 2011. This is a tiling at the infinity of hyperbolic space. The tiling is generated by reflections in 4 planes. The planes arrangement is obtained from faces of hyperbolic tetrahedron by truncating one vertex and one of opposite edges and moving points of truncation to infinity. The interplay of reflections forms circular area with infinitely many circular holes filled with two dimensional hyperbolic triangle tilings (2 3 24). To color the tiling we use different subgroups of the total symmetry group. --- Vladimir Bulatov

12 " X 16", Digital print, 2011. I began life as an art major. Much later I became interested in mathematics. When I bought my first computer I found that I could combine my love of art with my love of mathematics. The possibilities are endless. Here, attached to each point in a sequence of points along the lines $y = \pm x$ is a vector whose length and direction are determined by a complex function $h(x+iy)$. The color and transparency of the vector are functions of $\arctan(\textrm{Im}(h)/\textrm{Re}(h))$. --- Anne Burns

24" x 24", Archival Inkjet Print, 2011. This work is an exploration of the structure of the alternating group on five elements, and its particular presentation by two generators of orders 2 and 5. A stylized Cayley graph of this presentation of the group is shown over its dual graph. The regions in the dual image are colored according to the order of the element in the group. The image is constructed from multiple hand-drawn elements and natural textures which are scanned and digitally manipulated to form a composite image and subsequently output as an archival digital print. --- Conan Chadbourne

23cm x 21cm x 18cm, Faceted plastic beads and fish thread, 2008. Geometry is an essential ingredient of chemistry. The functionality of molecules depends heavily on their geometries. Here is the conjugate surface of the P surface. We chose to construct this surface in a tetrahedral form to avoid unconnected component. In contrast to the P surface, one can find this surface comprising helicoid units of two opposite chiralities, lining up along C2 axes. Octagonal rings are represented by green beads. --- Chern Chuang

20" x 20", Mixed media on canvas, 2011. This is a combination of Julia set fractal and droste effect. Julia Sets are one of the most famous types of fractals formed using formula iteration. The Droste effect depicts a smaller version of itself in a place where a similar picture would realistically be expected to appear. Combining the two effects brings visually significant occurrences explored sometimes more intuitively in medieval architecture, stained glass windows and weaving work . --- Jean Constant

Photograph, circa 1990. My area of interest is the application of mathematical concepts in technical applications of photography. Be it quantification of phenomena or the design and use of photography to visualize physical and mathematical concepts. A camera that rotated a circular piece of film past a radial slot acting as a shutter exposed the film for more than two rotations of the camera and thus recorded two plus views of the House grounds each covering a sector of about 120 degrees or so designed so that the 360 degree view of the grounds would produce a sector that could be cut and formed into a conical lampshade. Sometimes this photo is confused with those that a fisheye lens might make but the fisheye lens could only make a single image of the House per frame. Here there are two. --- Andrew Davidhazy

50cm x 50cm, Digital print, 2011. Seeking ways to illustrate mathematical concepts and constructions is an endless game. Jumping from one idea to another, mixing techniques and computer code, and then waiting for the image to appear on my screen, leads often to surprising results. Playing around with Apollonian gaskets, recursivity and circle inversion can give rise to landscapes no one has seen before. --- Francesco De Comité

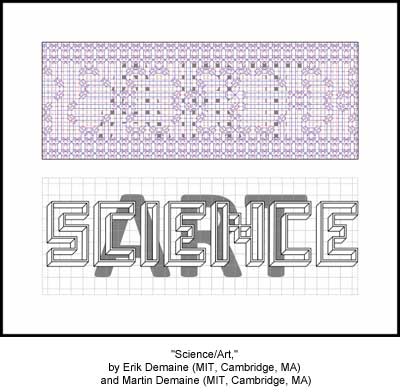
22" (tall) x 28" (wide), framed poster, elephant hide paper, 2011. The crease pattern (top) folds into both SCIENCE and ART (bottom, not to scale). More precisely, the rectangular paper sheet folds into the 3D structure of the word SCIENCE, while the gray inking in the sheet (top) forms the inked ART in the background (bottom). The message is that science and art can exist on a common plane, as two different perspectives of the same object. The crease pattern was designed using an algorithm by Demaine, Demaine, and Ku (2010), which describes how to efficiently fold any orthogonal "maze" (including word outlines like SCIENCE) from a rectangle of paper. Red lines fold one way and blue lines fold the other way. --- Erik Demaine

First Place Award - 2012 Mathematical Art Exhibition

20" x 26", Oil paint on canvas, 2011. It all arose from a sense of wonder when seeing the formal beauty of mysterious objects called polyhedra. Since then, I have joyfully played with geometric shapes and it led me to explore the possible representation of Geometry in classical painting. From Durer's magic square to strange cubes, painted by the precise brush of a would-be 17th century Dutch artist. --- Sylvie Donmoyer

11" x 11", Color printer, 2009. This is a hyperbolic pattern of butterflies, six of which meet at left front wing tips and four of which meet at their right rear wings. The pattern is inspired by M.C. Escher's Euclidean image Regular Division Drawing Number 70, and is colored similarly. Disregarding color, the symmetry group of this pattern is generated by 6-fold and 4-fold rotations about the respective meeting points of the wings, and is 642 in orbifold notation (or [4,6]+ in Coxeter notation). This pattern exhibits perfect color symmetry and its color group is S3, the symmetric group on three objects. --- Doug Dunham

50cm x 26 cm, Digital Print, 2011. A possible way to remove the gap between the worlds of sciences and humanities, is the search for interconnections between mathematics and physics with the sound and visual arts. This work is based on a family of algebraic surfaces with many nodal singularities. They have been introduced recently, by means of a kind of duality in the basic geometric constructions corresponding to the generation of substitution tilings ("A construction of algebraic surfaces with many real nodes". http://arxiv.org/abs/1107.3401). Here the surface is a nonic with 220 real nodes. In general, the surfaces have degrees divisible by three and cyclic symmetry. They appear as mirror pairs not necessarily topologically inequivalent (see the sextic with 59 real nodes in arXiv:1107.3401). --- Juan G. Escudero

16" x 16", Archival inkjet print, 2011. This artwork is based on a fractal tessellation of kite-shaped tiles I discovered several years ago. Grouping of the kite-shaped tiles into spirals allowed a fractal tessellation to be created in which two colors were sufficient to ensure that no two adjacent tiles have the same color. All of the spirals in the print have the same shape (more precisely, they are all similar in the Euclidean plane). --- Robert Fathauer

24" x 24" (framed), Archival inkjet print, 2011. Hybrid 101 is a representation of an invariant measure for a dynamical system on a 2-torus with deterministic and random components. Deterministic dynamics is given by the product of two identical circle maps with topological degree 2 ('doubling maps') together with a random component which is a place dependent iterated function system: probabilities and direction and size of jumps depend on the position on the torus. Hybrid dynamics combining deterministic dynamics with an iterated function system was first studied mathematically by Kobre and Young in the context of extended dynamical systems on the line. In Hybrid 101, dynamics is defined by doubly 1-periodic maps on the plane and we reduce mod the integer lattice to obtain dynamics on a torus. We lift the measure back to the plane to obtain a repeating pattern. Appearances can be deceptive: the only symmetries of the repeating pattern are translations (the pattern is of type p1) and all the lines are straight. --- Michael Field

Sizes vary from 1.5" to 2.5" wide by 5.5" to 8" long, Seed bead weaving, 2011. I weave beads to appeal to people's affinity for organization in design. I use mathematics, including geometry, symmetry, and topology, as an inspiration for the structure of my creations. In this series, I explore how tilings of the plane can be interpreted as beaded angle weaves. Tilings of the plane, especially periodic tilings, can be used as the basis for flat bead weaving patterns called angle weaves. The ?star tilings? used to design these five bracelets are generated from the three regular tilings of the plane and two other Laves tilings. I converted each star tiling into a star weave by placing beads on the vertices and edges of the tiling and weaving them together with a needle and thread. Because all of the vertices in a regular tiling are similar, all of the stars are similar in the three regular star weaves (i.e., Kepler's Star, Archimedes' Star, and David's Star). The other two star weaves (i.e., Night Sky and Snow Star) include stars of two types, reflecting the two types of vertices in their respective Laves tilings. --- Gwen Fisher

17" L x 11" H x 7 D", Steel, 2010. A sculpture is defined as a form in a position relative to a fixed horizontal plane (base, ground). To hypersee an outdoor sculpture, one walks around it to see overall views and close up detail views from different viewpoints as well as in different light conditions at different times. If two sculptures consist of the same form in different positions, then the sculptures are said to be congruent. Congruent sculptures can look so completely different that one does not realize the sculptures are congruent. A hypersculpture is a group of congruent sculptures, and a more complete presentation of the sculptural possibilities of a form. In order to hypersee a form, one presents it as a hypersculpture. This hypersculpture, Four Right Angles, consists of two vertical and three horizontal congruent sculptures and is discussed in an article "Hypersculptures: Four Right Angles" in the Spring issue of Hyperseeing. The two vertical sculptures, Ascent and Cantilever, are shown here in this gallery. The form consists of four identical angle iron sections welded together. Each section is 5" x 5" x 6 1/2", and 1/2" thick. ---Nat Friedman

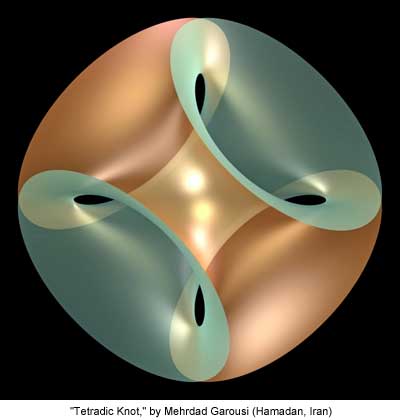
20" x 20", Digital Art Print, 2010. I am interested in all types of mathematical arts which are generated in computers; from 2D and 3D fractals to 3D mathematical sculptures and knots. Every now and then I encounter a new imagery software working on the basis of mathematical algorithms, I try to examine its capacities in creating works containing acceptable amounts of aesthetics. This time I have used Surfer, a mathematical imagery software which creates and displays surfaces constructed according to zero sets of polynomial equations. $$(x^2+y^2+z^2-(0.5+2a)^2)^2-(3((0.5+2a)^2)-1.0)/(3-((0.5+2a)^2))*$$

$$(1-z-\sqrt{3}x)(1-z+\sqrt{3}x)(1+z+\sqrt{3}y)(1+z-\sqrt{3}y)=0,$$

and $a = 0.15$. It should be noted that opening my equations in the software might not have the same result in your viewer. Differences are because of zoom, color, and/or position issues that are not contained in the equations. --- Mehrdad Garousi

3" x 3" x 3", Nylon (selective laser sintering), 2011. Four Sierpinski triangles interweave in three dimensions, each linked with, but not touching, the other three. The twelve outer vertices are positioned as the vertices of an Archimedean cuboctahedron and the black support frame is the projection of this cuboctahedron to the circumsphere. These are fifth-level Sierpinski triangles, i.e., there are five different sizes of triangular holes. The strut diameters were made to vary with the depth of recursion, giving a visual and tactile sense of this depth. This hand-painted maquette is intended as a model for a possible large outdoor sculpture. --- George Hart

12" diameter, needlepoint canvas, 2011. "Color Wheel with Twist" is more than just a stitched version of the artist?s color wheel, and is also more than the mathematician's non-orientable manifold. The colored leaves flow all around the band in their natural order on the color wheel; yet this mysterious shape has only one side. I wanted to capture both color theory and geometry in this piece. --- Diane Herrmann

Second Place Award - 2012 Mathematical Art Exhibition

16" x 16" x 5", elephant hide paper, 2011. Imagine a long paper cone that is pleated with alternating mountain and valley creases so that its cross-section is star-shaped. Now slice the cone with a plane and imagine reflecting the top part of the cone through this plane. The result is exactly what one would get if we folded the pleated cone along creases made by the intersecting plane. Doing this repeatedly can result in interesting shapes, including the origami version presented here. This work is a collaboration. The concept and crease pattern for this work was devised and modeled in Mathematica by origami artist Robert Lang. The crease pattern was then printed onto elephant hide paper by artist Ray Schamp). The paper was then folded along the crease pattern by mathematician and origami artist Thomas Hull. Part of the charm of paper folding is its capacity for simple, elegant beauty as well as stunning complexity, all within the same set of constraints. This mirrors the appeal of mathematics quite well. Geometric origami, which is where most of my artwork lives, strives to express in physical form the inherent beauty of mathematical concepts in geometry, algebra, and combinatorics. The constraints that origami provides (only folding, no cutting, and either one sheet of paper or further constraints if more than one sheet is allowed) challenges the artist in a way similar to being challenged be a mathematical problem. --- Thomas Hull

12" x 12" x 12", printed paper, 2011. My artworks are based on investigations into mathematical form concerning the arrangements of units in space. This is a model of a triacontehedron using minimal surface planes with an infinite regression pattern. --- Richard Kallweit

6" x 16", Archival Inkjet Print, 2011. The traditional quilt pattern "Broken Dishes" and certain edge-matching puzzles share a common visual element ? a square subdivided along its main diagonals to form 4 right triangles. This work presents 4 puzzle solutions using this visual element in a format suggesting Broken Dishes quilts. Edge-matching puzzles based on the square were introduced by MacMahon in the 1920s. One challenge was to arrange a set of 24 three-colored squares (all the possibilities) in a rectangle with same colors matching on the edges and a single color appearing around the border. If this is generalized to four colors, the complete set of puzzle pieces jumps to 70. These can be arranged in a 7x10 rectangle, providing a nice quilt proportion. This set of four designs is based on different matching ?rules? ranging from strict matching to random placement, while maintaining the border requirement. To produce richer colors, each design is overlaid with a translucent scrim of the next design in the sequence. --- Margaret Kepner

9" x 6" x 12", folded book, 2011. Folded Book Sculpture. The collection of folds forms an envelope to the parabola. The abounding waves emanate as the book is opened and spread out. --- Sharol Nau

8" x 8" x 8", Selectively Laser Sintered Nylon, 2011. We designers at Nervous System are attracted to complex and unconventional geometries. Our inspirations are grounded in the natural forms and corresponding processes which construct the world around us. Laplacian Growth #1 is an instance of growth using a model of 3D isotropic dendritic solidification. The form is grown in a simulation based on crystal solidification in a supercooled environment. This piece is part of a series exploring the concept of laplacian growth. Laplacian growth involves a structure which expands at a rate proportional to the gradient of a laplacian field. Under the right circumstances, this leads to instabilities causing intricate, fractal branching structure to emerge. This type of growth can be seen in a myriad of systems, including crystal growth, dielectric breakdown, corals, Hele-Shaw cells, and random matrix theory. This series of works aims to examine the space of structure generated by these systems. --- Nervous System generative designers

60cm x 60cm, Digital Print (Hahnemuhle Canvas Goya). Eleph-Zero and its clones are tessellations of the plane made with the crystallographic group P3. With this work I wanted also to illustrate links between Algebra and Topology. Eleph-Zero walks on two spirals from the south to the north. --- Dominique Ribault

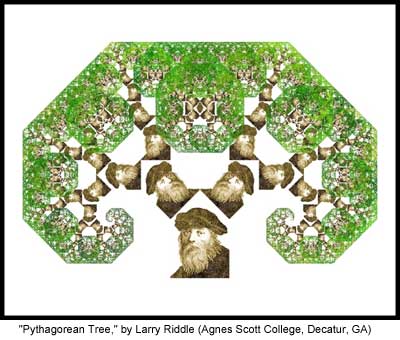
16" X 20", Digital print, 2011. The traditional Pythagorean Tree is constructed by starting with a square and constructing two smaller squares such that the corners of the squares coincide pairwise (thus enclosing a right triangle), then iterating the construction on each of the two smaller squares. When viewed as an iterated function system, however, one can start the iteration with any initial set. For this image I began with a common picture of Pythagoras as the initial set. The trunk of the tree was constructed using 10 iterations of a deterministic algorithm based on an iterated function system with three functions - the identity function, a scaling and rotation by 45 degrees, and a scaling and rotation by 45 degrees with a reflection. This gives a reflective symmetry for the trunk. The leaves consist of 500,000 points plotted using a random chaos game algorithm and colored based on a "color stealing" algorithm for iterated function systems described by Michael Barnsley in a 2003 paper. To give the leaves a realistic shading, the colors were from a digital photograph of a field of green and yellow grass. -- Larry Riddle

20" square, Digital Print on metal, 2011. I am particularly interested in creating visualizations of data and of mathematical structures, and more broadly in the creation of art directly from code. It has long been observed that a logarithmic spiral describes a snail shell quite well. I created this image as part of a series of pieces based upon logarithmic spirals. --- Ian Sammis

16" X 20", Digital print, 2011. I am interested in Persian geometric art and its historical methods of construction, which I explore using the computer software Geometer's Sketchpad. I then create digital artworks from these geometric constructions primarily using the computer software PaintShopPro. Kharragan is an artwork based on a design on one of the 11th century twin tomb towers in Kharraqan, western Iran. The artwork demonstrates two different approaches that are assumed to have been utilized centuries ago to create the layout of the pattern, which is at the center of the artwork. From left to right, the artwork exhibits the construction of the design based on a compass and straightedge. From right to left, we see another approach, the Modularity method, to construct the same design using cutting and pasting of tiles in two colors. --- Reza Sarhangi (1952-2016)

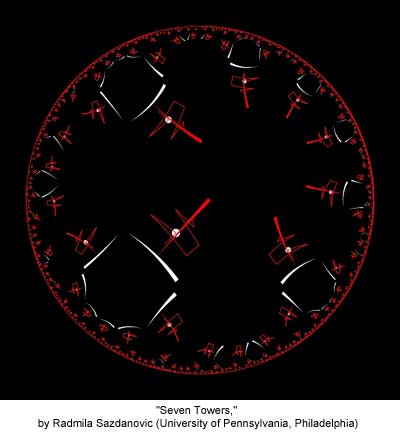
16" x 16", Digital Print, 2011. This tessellation of the hyperbolic plane is inspired by Japanese pagodas but realized in classical black, red and white color scheme, emphasizing local 7-fold symmetry. --- Radmila Sazdanovic

152mm x 62mm x 109mm, PA 2200 Plastic, Selective-Laser-Sintered, 2011. My mathematical research is in 3-dimensional geometry and topology, and concepts from those areas often appear in my work. The usual version of a Möbius strip has as its single boundary curve an unknotted loop. This unknotted loop can be deformed into a round circle, with the strip deformed along with it. This shows a particularly symmetric result. The boundary of the strip is the circle in the middle, and the surface "goes through infinity", meaning that the grid pattern should continue arbitrarily far outwards. To save on costs, I have removed the grid lines that would require an infinite amount of plastic to print. --- Henry Segerman

4" x 6", Archival Pigment Print, 2011. I love to experiment in the fuzzy overlap between art, mathematics, and programming. Seeking to extract and visualize the beauty that I glimpse beneath the surface of equations and systems, I create custom interactive programs and use them to explore algorithms, and ultimately to generate artwork. When I prepare an image from my Aesthetic Explorations series of strange attractors for print, the first step is rendering a very high resolution, high quality 16-bit grayscale image from my custom software. While these images are destined to spend some time in Photoshop in a process of recoloring and enhancement, I find that they are very beautiful in and of themselves. The nature of algorithmic artwork (and fractal phenomena in nature in general) is that there is captivating detail at all scales. This is a crop from "Trefoil". --- Nathan Selikoff

Third Place Award - 2012 Mathematical Art Exhibition

" x 6" x 4.5", FDM model, 2011. My professional work in computer graphics and geometric design has also provided a bridge to the world of art. This is a gridded model of a Klein bottle (Euler characteristic 0, genus 2) with the minimal possible total surface bending energy. This energy is calculated as the surface integral over mean curvature squared. --- Carlo Séquin

24" x 36", quilt, 2011. Our quilts are based on "Rule 30" (in Wolfram's classification of elementary cellular automata), applied to a cylindrical phase space. "Winter" is the basic rule 30 to produce a two-color pattern. The successive patterns combine the history of two ("Spring"), three ("Summer), or four ("Fall") generations to produce a palette of four, eight, or sixteen colors. In this quilt, "Spring", the colors are determined by the history of a cell at times t = 2k and 2k + 1, treated as a two-bit number between 0 and 3. --- Jeff Suzuki and Jacqui Burke

Print from digital, 2011. 'The smoothness spiral' is an interactive applet that plots the first 10,000 integers on an Archimedean spiral. Each point has a brightness depending on its number-theoretic smoothness (its largest prime divisor), controlled by a user-selected threshold. Curves of smooth numbers emerge, whilst large primes are conspicuous by their absence, causing 'missing' curves. This print from 'the smoothness spiral'; the threshold is set to show values which are at most 101-smooth, with brightness proportional to smoothness. --- Graeme Taylor

Panoramic Photograph, 2011. I've been exploring recent developments in digital imagery which allow me to utilize mathematics and computer programming to solve visual problems. This is a projection made from a panorama of 13 photographs. The individual photos were shot from precisely the same point in space, and when stitched together they comprise the entire "viewable sphere" centered at that vantage point. That is, the panorama has complete coverage of the scene--360 degrees around, and 180 degrees from top to bottom. Stereographic projection was then applied to the spherical panorama, with the projection taken from the North Pole so that the point directly overhead becomes the point at infinity. This produces a lovely "little planet" effect, with the geometry of the roof structure framing the scene. The panorama was shot at Oriente Station in Lisbon, Portugal. --- Bruce Torrence

Craft Foam, 2010. I love the symmetric beauty of polyhedra and enjoy creating models to study. Through the process of building a model I am able to truly understand its form. I like to use color to help reveal the structure and patterns of an object. This sculpture is based on the third stellation of the dodecahedron. A stellation of a regular polyhedron is formed by extending the faces until they intersect and enclose a region of space. The faces of the dodecahedron will intersect three times as they are extended, forming the small stellated dodecahedron, the great dodecahdron, and the great stellated dodecahedron. Twelve identical pieces of craft foam were slotted at the edge of each stellation and then tightly woven. This open skeleton allows one to follow each face to view the intersections and the outline of the dodecahedron and the three stellations. Six colors of foam are used and parallel faces are the same color. Each of the five arms of each face intersects three others to form 20 colorful "flames" in an icosahedral arrangement. --- Eve Torrence

Laser-etched glass, 14 items, 12cm diameter each, 2011. The advent of accessible automated tools opens up a number of new approaches to art: especially algorithmic and mathematical art works. The computational control allows us to write algorithms to generate concrete physical art; and their precision allows a higher resolution than what the eye can discern. These pieces highlighting and reifying different mathematical concepts, giving them physical presence and accessibility and turning abstract geometry into hands-on displays and objects. Among the most successful of the reified mathematics art-pieces I produced where these--hyperbolic disk tilings with the Poincare disk model were etched onto glass disks, producing a collection of reified hyperbolic geometries and symmetries. --- Mikael Vejdemo-Johansson