
Mathematical ImageryMathematical artists create strong, stunning works in all media and explore the visualization of mathematics
2019 Mathematical Art Exhibition
The 2019 Mathematical Art Exhibition was held at the Joint Mathematical Meetings held in Baltimore, MD. Here on Mathematical Imagery is a selection of the works in various media, including recipients of the 2019 Mathematical Art Exhibition Awards: "Roundabout (1211+2333+3122) (O+G on R+BG-YG)" and "Roundabout (1332+2121+3213) (V+O on YG-BG+V-R-O)," (pair) by James Mai, awarded Best photograph, painting, or print; "DT-MSH/TC Klein Bottle," by Elizabeth Paley, awarded Best textile, sculpture, or other medium; and "Breaking the Ruled," by Matt Enlow, Honorable Mention. The Award "for aesthetically pleasing works that combine mathematics and art" was established in 2008 through an endowment provided to the American Mathematical Society by an anonymous donor who wishes to acknowledge those whose works demonstrate the beauty and elegance of mathematics expressed in a visual art form.

5 x 20 x 20 cm, paper, 2000. This wreath was designed and folded by Bennett and assembled by Rona. It is made from 240 copies of one module. The wreath consists of ten truncated octahedra linked together in a ring. Each truncated octahedron is made from 24 One Piece Triangle modules (designed by Bennett Arnstein). Red modules are scattered throughout the model to suggest berries. The green modules suggest leaves The modules are made from equilateral triangles and hold together without glue. The modules have pockets and tabs that are produced by folding alone. --- Bennett Arnstein and Rona Gurkewitz

40 x 50 cm, inkjet print on canvas, 2018. The underlying polyhedral shapes are an octahedron, a cuboctahedron, and one made from 18 squares and eight triangles. Each polyhedron has a path that visits all the edges once and only once, returning to its original vertex. A rainbow of line segments then tracks its progress along this Eulerian circuit! Follow the journey with your eyes. Can you see the squares that lie on a cube, or the triangles sitting at the corners of a cube? (This scene is viewable in 3D or VR.) --- Dan Bach

18 x 33 x 33 cm, knitted wool yarns, 2018. I am a mathematician who knits as well as a knitter who does mathematics. These are knotted Klein bottles--specifically, each is a figure-8 knotted figure-8 embedding of the Klein bottle. One was constructed by knitting a figure-8 (self-intersecting) tube and wrapping it into a figure-8 knot before grafting the tube into a Klein bottle, so it is an intrinsic figure-8 embedding and an extrinsic figure-8 knot. The other was constructed by knitting a figure-8 knotted Möbius band and grafting the boundaries into a figure-8 embedding of the Klein bottle, so it is an intrinsic figure-8 knot with an extrinsic figure-8 embedding. (Can you tell which is which?) That is, this pair of objects was made so that one could say that each is an intrinsic and extrinsic figure-8, but in different ways! --- sarah-marie belcastro

12 x 12 x 4 cm, 3D printed nylon plastic, 2018. A non-self-intersecting Hamiltonian cycle on a self-intersecting Möbius strip having five one-quarter twists the first time around, and then another five one-quarter twists the second time around. --- Robert Bosch and Ari Smith

45 x 45 x 45 cm, laminated wood/ styrene, 2014. This sculpture demonstrates my technique of building 3D-Lissojous figures. I first saw these figures on the screen of an early oscilloscope, flat curves describing, for example, a spinning coin or a gyrating hula hoop. I then imagined how I might describe these Lissajous in 3D, and then how to actually build them as sculpture. Lines and curves in this work are constructed as laminations of thin strips of wood and/or other materials. In this case the inner layer is cherry, middle layers styrene, and the outer layer is rosewood. Strips are assembled as a bundle with fresh epoxy glue between layers, are bent as a bundle around a math-defined form, and then allowed to harden into final form. The Dancers stand on a "floor" of brown velvet, and the turntable base turns to see them dance. 3D Lissajous sculptures are unique to my work. --- Fielding Brown

28 x 30 x 30 cm, painted glass (fired in a kiln), stainless steel and wood 2018. A laser beam fired through a certain type of crystal can cause individual photons, at the quantum level, to be split into pairs of entangled photons....actions performed on one affect the other, even when they are separated by great distances. My piece, "Entangled", depicts two pairs of entangled particles. I painted (and fired in a kiln) 2D de Bruijn 4 X 4 arrays (window length four) on two clear glass panels, with spinning red and yellow particles in the corresponding 2 X 2 windows - separated by the space between the panels. For one of the pairs, one of the photons has been "observed/measured". From observation of the painted particles, you can determine which of the two painted pairs has been "measured". --- Bronna Butler

2 x 9 x 9 cm, paper, 105 gsm, wood, clear acrylic, 2018. I have been fascinated by origami, and especially origami as a medium to explore geometry, since I was a child. This design stemmed from learning about Islamic tessellations in a Seminar class at my high school, and further experimentation with folding paper. I discovered a simple fold that allowed the paper to be folded orthogonally, and eventually devised a pattern that could be repeated indefinitely on a square grid. Viewed from above, the tessellation can be taken as a tiling of two different irregular octagons and a 2:1 rectangle, with squares nestled within the larger, recessed octagons. Unlike many other origami tessellations, this work takes great advantage of the third dimension, stepping up and down in height regularly. --- Derek Chen

30 x 32 cm, acrylic plastic, nail polish, 2018. This is a periodic billiard trajectory on the regular pentagon. The trajectory goes straight until it hits an edge, and then it bounces following the usual billiard rule that the angle of incidence equals the angle of reflection--and in this case, it switches to the other side of the piece and changes color. Equivalently, if you had a ribbon that was red on one side and blue on the other and wrapped it around the table, this is the picture you would get. The two colors are mirror images of each other. When I show people a list of hundreds of periodic billiard trajectories and ask them which one is the most beautiful, about half of the people choose this one (or a similar one in the same family). Periodic paths on the pentagon are so beautiful that I wanted to get them off the screen and into people's hands. I have made hundreds of pairs of earrings, and other objects decorated with these billiard pictures. --- Diana Davis
![D2_02 [fuzzy fibonacci], by Hans Dehlinger](https://www.ams.org/images/jmm19-dehlinger.jpg)
19 x 19 cm, digital print on archival paper, 2016. The focus of my work is on generative art based on algorithms. This image is based on the numbers 1 - 1 - 2 - 3 - 5, which are at the beginning of the well known Fibonacci Sequence. Mathematically it is rather simple - however, quite amazing opportunities from an artist´s point of view are resulting. The underlying line-drawing is generated with a program (Python), and its parameter settings determine angle, number of lines in sections, repetitions, rotations, and so on. The mathematical starting point and the strict generative-algorithmic production process are on the one side; the addition of intuitive artistic judgement is on the other side. --- Hans Dehlinger
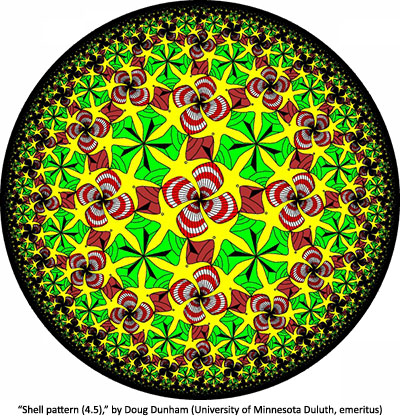
30 x 30 cm, aluminum print, 2108. This hyperbolic pattern is inspired by Escher's Regular Division Drawing number 42. There are obvious 5-fold rotation centers at the meeting points of the conchs. However the apparent 4-fold meeting points of the cockles are actually only 2-fold rotation centers since the openings of the adjacent snails alternately point toward and away from those centers. This preserves Escher's symmetry in Drawing 42 in which there are two kinds of 4-fold rotation centers at the meeting points of the conchs. Similarly, in this pattern there are two kinds of 5-fold rotation centers at those meeting points, those at which the tips of the conchs touch the openings of the snails and those at which the tips point away from the snail openings. --- Doug Dunham
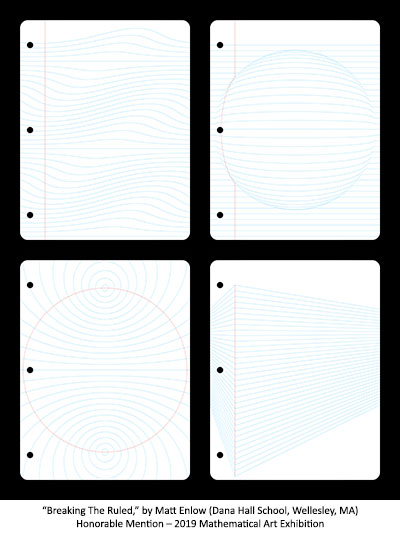
Honorable Mention - 2019 Mathematical Art Exhibition
64 x 51 cm, paper, 2018. Appropriately enough, I was inspired by Marc Thomasset’s “Inspiration Pad.” I was taken with the idea of taking an everyday object—a sheet of standard ruled paper—and “remixing” it to create something new and unique. The ubiquity and familiarity of the original object make the resulting images all the more arresting. I created the images in Mathematica, and printed them on standard printer paper. I then hand-cut the corners, and hand-punched the holes. More information. --- Matt Enlow

51 x 61 cm, digital print on aluminum, 2018. I modified a simple formula for creating regular polyhedral meshes from a symmetric set of points and arrived at the "shrink-wrap" appearance of the dodecadedral shape, rendered here in granite and in crystal. (The input to the mesh algorithm is the set of dodecahedral face centers.) The sphere is decorated with the same symmetry, using a collage of flower photographs as the base image. I placed a copy of the sphere inside the crystal shape, aligning by symmetry, and waited about a day for ray tracing to create all the marvelous reflections. The tromp l'oeil frame uses Fourier series, a photograph of wood grain for texture, and more hours of ray tracing. For me, the scene evokes the synergy of elements that give us life. --- Frank A. Farris

25 x 25 x 25 cm, ceramics, 2018. Mathematical structure is evident throughout the natural world. My work explores the mathematics of symmetry, fractals, tessellations and more, blending it with plant and animal forms as well as inorganic forms found in nature. This synthesis allows me to create innovative prints and sculptures that derive their beauty from a combination of complexity and underlying order. This piece was inspired by electron micrographs of pollen grains such as dandelion, chicory, and stitchwort. It has approximate icosahedral symmetry. --- Robert Fathauer

31 x 16 cm, merino/alpaca yarn, glass beads, 2018. There are two things I have done for as long as I can remember: explore mathematics, and create things with my hands. The Fundamental Frieze Scroll series follows in the footsteps of earlier pendants depicting the seven frieze groups in knitted lace. In those works, each of the seven designs occupies the same amount of space, regardless of complexity. Here, each frieze design is generated by the same fundamental region, a rectangular pattern with no internal symmetries. Each design uses only enough copies of this rectangle to generate three translations of its primitive cell. In Fundamental Frieze Scroll I, the fundamental region design is a lace rendition of a Truchet tile, a rectangle divided along a diagonal into light and dark triangles. Truchet tiles appear in many recent mathematical artworks, including Carolyn Yackel's lace knitting. --- Susan Goldstine

23 x 15 cm, digital print, 2018. After placing a finite number of chips at each vertex of a finite graph, a chip firing cellular automaton is defined by iterating the rule: every vertex that has at least as many chips as neighbors distributes one chip to each of its neighbors. When the graph is a cycle with thirty vertices, and initially a vertex can have at most three chips, then after the transient phase the period is always one, two, or thirty. Therefore the question of interest is: how many iterations can the transient phase last? This period two automata is an example where the transient phase lasts for the conjectured maximum of ninety iterations. Vertices are colored white, yellow, orange, or red according as they have 0, 1, 2 or 3 chips. --- Gary Greenfield

30 x 90 x 30 cm, lasercut mylar, 2018. Triply periodic surfaces are strange, beautiful three dimensional structure. Here a single unit the 6-branch Curvahedra piece, is put together always linking together in loops of 4, to give approximations of the Schwartz D, Gyroid and Schwartz P minimal surfaces. The difference simply in how the structure loops back on itself as a surface, giving three quite different surfaces, two discovered by Schwartz and one, lying between them as you transform from one to the other, by Alan Schoen some time later. This might be the first time all three have been made from a single system. --- Edmund Harriss

30 x 25 x 25 cm, paper, mdf, steel, magnet, 2018. The left figure shows the paper-crafted catenoid surface and that of the helicoid is shown in the right. What is interesting here is that these surfaces can be transformed isometrically with each other, i.e. shape transformation without any straining. This is because the first fundamental form of the surfaces are identical. I made this model from weaving paper strips. The shape of the strips are obtained by minimizing the strain energy defined on a Riemannian manifold. The optimization problem is solved numerically using NURBS-based isogeometric analysis. This artwork is transformable, and thus the dimensions mentioned above are maximum sizes. The shape of the artwork will be sometimes changed by exhibitor during the event. --- Yuto Horikawa

10 x 23 x 23 cm, two sheets of Lokta paper, purple and green, back-coated together with methylcellulose, 2018. This model was designed by Thomas Hull and folded by Robby Kraft. It is folded from a regular octagon. The crease pattern is a geometric progression of inscribed squares in an octagon, with the symmetry lines of the octagon included as creases. In theory, the crease pattern can be continued infinitely to the center. The model is also iso-area, which means that the same folded pattern is made on both sides of the paper. To achieve this model, Kraft glued two sheets of Lokta paper, one purple and one green, back-to-back using methylcellulose. --- Thomas Hull and Robby Kraft

110 x 110 cm, textiles – quilting, 2018. The Poincare disk admits many interesting tilings. This octahedral tiling corresponds to the universal cover of the two-holed torus, the colors were chosen to reflect this interpretation of the tiling. If the large colored regions of the same color were identified, the central white region would form a two holed torus. If we identify the edges between the smaller colored regions with elements of the fundamental group of the two holed torus the colors of the smaller regions are determined by the fundamental group elements crossed as we move out from the central white region. --- Kate Ponto

40 x 68 cm, archival inkjet print, 2018. A square spiral structure provides the basis for this piece. Each of the two spirals grows outward (from a central square representing “one”) in a sequence of trapezoids culminating in the 101st one at the top. In the left-hand spiral, regions corresponding to prime numbers are colored cyan, while those belonging to other number sequences (happy, triangular, and Fibonacci) are assigned the colors magenta, yellow, and transparent white. Integers that are associated with more than one sequence result in mixed hues. On the right-hand side, the direction of the spiraling trapezoids is reversed, and a different selection of integer sequences is represented. These are the lucky, harshad, generalized pentagonal, and Lucas numbers. --- Margaret Kepner

15 x 15 x 15 cm, vero polyjet, 2018. In mathematics, the Mandelbox is a fractal with a box-like shape. Its definition is similar to that of the Mandelbrot set. Both are sets of values of a parameter such that the origin does not escape to infinity under iteration of certain mathematical operations. The Mandelbox is defined as a map of continuous Julia sets, but, unlike the Mandelbrot set, can be defined in any number of dimensions. Although the concept of the Mandelbox has been around since 2010, this novel artwork implants such a box in a physical space. It overcomes the lack of connectivity between parts of the object by applying recent breakthroughs in 3D printing, allowing the printing of a polychromatic fractal within the clear plastic. After printing, I hand polished it. --- Cole Kissane

15 x 15 cm, digital print on wood, 2017. The relaxation unfolds as one begins to cultivate an appreciation for the purity of line and the poetry of flowing motion. The eye is led into a controlled, orderly procession of the design components as they wheel around the central point; you become caught up the rhythm of the universe. The healing power of mandalas is at times even more profound, for the geometric designs they reveal are eternal patterns brought into existence in such forms as snowflakes, flowers, starfish, seashells, and Rams’ horns. More information --- Robert Krawczyk

21 x 48 x 1 cm, paper, decorative paper, glue, and book cloth, 2018. This 4-column thread book hides 19 expandable compartments. The elegant ways the various layers of these thread books interact with each other intrigues me. Instructions for constructing them have been hard to come by, largely because Zhen Xian Bao have only been recently introduced in the West. When I have found instructions, a basic style is taught, using specific measurements. It's been my quest to generalize the relationships between the boxes, all of which are based on the square, so as to be able to create many variations. In so doing, I've discovered that using precisely scaled Islamic geometric designs on the papers enables me and my students to better see the relationships we need in order to create our own versions of Zhen Xian Bao. --- Paula Beardell Krieg

Best photograph, painting, or print - 2019 Mathematical Art Exhibition (pair of works)
"Roundabout (1211+2333+3122) (O+G on R+BG-YG)" (left) and "Roundabout (1332+2121+3213) (V+O on YG-BG+V-R-O)," by James Mai, are 20 x 20 cm, archival inkjet prints, 2018.

20 x 20 cm, archival inkjet print, 2018. This composition uses the loop-form as a compositional matrix to explore color relativity. Orange and green colored lines (loops 1211 and 2333, respectively) cross into red and greenish color areas (loop 3112 and the large circular field). Although the orange and green lines are physically invariant in color, they appear to change from warmer to cooler and lighter to darker because of the influence of the colored grounds. --- James Mai

20 x 20 cm, archival inkjet print, 2018. This composition uses the loop-form as a compositional matrix to explore color relativity. Violet and orange colored lines (loops 1332 and 2121, respectively) cross into greenish and reddish color areas (loop 3213 and the large circular field). Although the violet and orange lines are physically invariant in color, they appear to change from warmer to cooler and lighter to darker because of the influence of the colored grounds. --- James Mai

16 x 18 x 18 cm, 3D printed nylon plastic, 2018. Five racks, each with two beams, slide through each other in this one degree-of-freedom mechanism. In Thurston-Conway orbifold notation, this has symmetry type 5x. Thanks to John and Jane Kosticks for telling us about the geometry this is based on. --- Elisabetta Matsumoto and Henry Segerman

40 x 40 cm, digital print onto aluminum panel, 2018. My work is composed primarily of computer generated, mathematically-inspired, abstract images. I draw from the areas of geometry, fractals and numerical analysis, and combine them with image processing technology. This image examines the chaotic nature that Newton's method can exhibit. Here, the routine attempts to solve a system of two real equations in two variables, using the matrix formulation of Newton's method. The method has been augmented through the inclusion of a matrix weight, whose elements were chosen to prevent finding a solution. A complex number was formed using the variables as components and the image was colored by the polar angle of the complex combination. --- Kerry Mitchell

23 x 18 x 10 cm, black ash basketry, 2018. I prepare my weaving materials by hand, beginning with a freshly cut black ash log. Layer by layer, I remove the growth ring fractals, reduce them to narrow strips of splint, and reassemble them into woven forms bearing tessellations, fractals, and other patterns that can be achieved with knotting, twills, triaxial layering, curled surface embellishments, and other weaving methodologies. My material preparation techniques were learned 30 years ago from a Potawatomi elder. Here multiple layers of triaxial weaving with algorithmic color placement creates a repeating self-similar triangular tessellation. A slight curve introduces three-dimensional Euclidean space which is further augmented by the infinitesimal rotation of vector fields with clockwise and counter-clockwise circulation. This piece is made of hand-pounded black ash in natural, cobalt blue, and bronze. Colors are achieved with fiber-reactive dye which binds with the cellulose in the wood splint. The weaving is mounted in a black shadow box for easy display. --- Marcia Morse Mullins

17 x 15 x 13 cm, folded book, 2018. Folded books serve to illustrate the beauty of Longest Crease, Parabola and Spirals without destroying the books but re-purposing them as sculptures. In this folded book, Quotable Woman, a spiral of Archimedes is formed along the top edge and a cylindrical helix along the front. Furthermore, there’s an internal conical helix (not visible) produced by points to which the active corners of the pages are folded. --- Sharol Nau

22 x 45 x 4 cm, stardream paper, 2018. Wiggle is the first design in my Linear Wave series, a collection of flat-foldable origami corrugations that model a raised, nonlinear curve when expanded, and appear linear when in the flat configuration. Other designs in this series include a sine wave, square wave, and Hilbert curve. I am currently developing the method to model any continuous function. Wiggle is based on tangent semicircles. The upper portion of the image shows the extended pattern and the lower portion shows the same pattern fully folded. If this design were folded from zero thickness paper, it would be completely planar and the lower portion would show only a vertical line. Instead, the "wiggle" is collapsed down to a central horizontal line. More information. --- Uyen Nguyen

40 x 40 x 3 cm, stardream paper, 2018. This origami corrugation was designed using the method presented in the Bridges 2018 paper, "Origami Explorations of Convex Uniform Tilings Through the Lens of Ron Resch's Linear Flower," by Uyen Nguyen and Ben Fritzson. It was modeled after a k-uniform tiling and its dual. The complex units form a 3-isogonal tiling [34 6; 3342; 324.3.4] and the simple units form the dual tiling, which is comprised of three different types of pentagons that can tile the plane: Floret (Type 5), Cairo (Type 4), and Prismatic (Type 1). Individually, each of these pentagons form Catalan tilings. Because the arrangement of these pentagons has hexagonal symmetry, the work is titled Pentagonal Honeycomb. It is folded from one sheet of paper. --- Uyen Nguyen
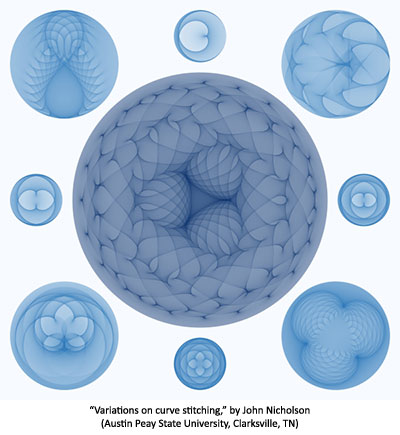
41 x 41 cm, inkjet on aluminum, 2018. In curve stitching, N points are drawn on a circle. Line segments then connect points I to points ((K * I) mod N), with a cardioid appearing when K = 2. Usually, N is kept low and the line segments are visible. In this work, N is essentially infinite. Line segments and points on the segments are randomly sampled and displayed as a density plot. The small center circles on the borders are the result of multiplying by K = 3/2, 5/3, 7/5, and 11/7. The corner and center variations are created similarly except they connect points on a circle to points on different types of curves: a lemniscate (top left), two different rose curves (top right and bottom left), a hypocycloid (bottom right), and a hypotrochoid (center). --- John Nicholson

Best textile, sculpture, or other medium - 2019 Mathematical Art Exhibition
16 x 23 x 19 cm, stoneware, 2015. This Klein bottle representation was constructed from two wheel-thrown tori that were cut, assembled, and pierced. After bisque firing, the "mouth" of the bottle was lightly airbrushed with a copper-green glaze. The form was then fired in a wood-fueled kiln to ~2240°F. Soda ash was added late in the firing process; sodium ions from the ash react with silicates in the clay to produce a glassy finish. The form was later re-fired in a wood kiln to ~2350°F to achieve a glassier surface. The variations in surface color arise from the firing process, which induces orange "flashing" on the white clay and can fortuitously capture carbon, copper, and other elements from the kiln atmosphere. --- Elizabeth Paley

55 x 55 x 40 cm, wood and cotton, 2017. I am dedicated to fully exploring the possibilities of three dimensional shapes formed by straight lines. Symmetry makes it easier to suspend a form in midair as the forces pull it in all directions equally. I was drawn to this piece by the challenge of creating two ruled surfaces that were topologically similar and wanted to float 3 wooden frames in one piece. I usually suspend only two wooden shapes. The piece demonstrates the concepts of ruled surfaces and tensegrity and finished up as a very meditative piece. --- David H. Press

30 x 10 x 10 cm, 3D printed transparent resin, 2018. My latest experiments blend traditional sculptural techniques with 3d printing and laser scanning. Latest SLA 3D printing technologies allow me to 3D print in transparent resin that helps a lot in the visualization of the internal structure. This sculpture is made from toroidal warping of a truncated Scherk minimal surface. The two symmetrical shapes are placed in opposite directions to resemble a "clessidra" the Italian term for hourglass. --- Davide Prete

51 x 51 cm, digital print, 2018. I enjoy giving visual representations to abstract mathematical concepts such as number, form, and process. This work explores a quotient space group of the symmetry group 442 (p4) and its some of its normal subgroups. Each flower petal represents a subgroup element. --- David Reimann
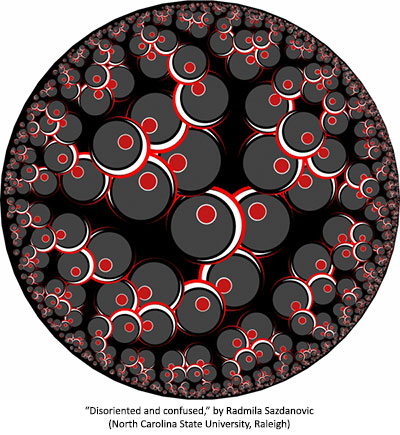
50 x 50 cm, computer graphics, 2018. The geometry and combinatorics behind tessellations provide the framework for creative, artistic expression. Sometimes, the choice of a particular motif can alter or hide the mathematical structure, obscuring or enhancing internal symmetries. Disoriented and Confused is based of hyperbolic tessellation (3, 4, 3, 4, 4) combined with patterns of increasing complexity and size. The mathematics and the algorithm behind the software Tess are determining the order in which the circles are drawn, hence the appearance of the artwork as a whole. --- Radmila Sazdanovic

19 x 19 x 19 cm, ABS, 3D-print, 2018. I start with the simplest Borromean soap film surface and place a smaller copy inside so that they just touch. To obtain a proper border configuration for a 2-manifold, I transform the six areas where two ovals touch into skewed crossing of two smooth curves. This results in a border curve system consisting of six simple interlinked loops. I force these loops to be perfectly circular, and then construct a soap-film on this border structure. To enhance the transparency of this sculpture and allow a better look at the inside geometry, I also cut out eight small circular holes from the two sets of 3-sided face patches in the outer and inner levels of the soap film. The 2-manifold is single-sided, of genus 6, and has 6+8 punctures. --- Carlo Séquin

27 x 27 cm, embroidery, 2018. This pattern of fish was inspired by M.C. Escher's "Circle Limit III" print which was based on the regular hyperbolic tessellation {8,3} of octagons meeting three at a vertex. In contrast, our pattern is based on the {10,3} tessellation, and thus has five fish meeting at right fin-tips instead of four as in Escher's print. Each backbone arc is an equidistant curve - a circular arc that is a constant hyperbolic distance from the hyperbolic line with the same endpoints on the bounding circle. The arcs curve to the left since there are more fish on the right. Our pattern requires six colors instead of the four that Escher used in order to achieve (perfect) color symmetry. In fact, the color symmetry group is the symmetric group A(5). Such patterns present considerable challenges for the embroiderer. The features become smaller as the bounding circle is approached and not all features can be included. The detail level drives a desire for the largest possible scale of the embroidery, which comes with a cost in complexity of implementation. The stitches must also be oriented to maintain the symmetry of the original design. --- Lisa Shier and Doug Dunham

12 x 9 x 1 cm, aquatint, 2015. This print began as an abandoned copper plate, riddled with imperfections and acid damage. By scraping and burnishing out flaws I was able to restore the copper to an engravable matrix. Pairing the aquatint process with the steps to create a Torus, allowed me to calculate out my inverse design. A marker is used to draw on the copper and is dunked in acid for 1 second, appearing white in the print. Then a second round of marks are made and will appear darker. Repeat this process in a series of timed baths for 1, 2, 4, 8, 16 seconds to produce gradients. The plate is then cleaned, inked, and pressed. It is this complex, sensitive, and manipulatable formula of aquatinting that inspired me to restore beauty to an abandoned object using mathematics. --- Dustin Wayne Clifford Skillman

50 x 50 cm, mixed media, 2018. Looking down on this Dimotorp, we can see I constructed it with twenty-four polygons. Each shape pivots fifteen degrees from the centre of one of its sides. This illustration is—like the preceding one—truncated after one complete rotation, at the twenty-six-sided cylinder. The height of the structure is finite because I maintained the same-size ratio between the polygons. I achieved an architectural appearance of a building’s stories by extruding each polygon the same height. --- Andrew Smith

4 x 20 x 20 cm, 3D printed nylon plastic, 2018. "Near plane crash" is a piece that I designed in OpenSCAD and had printed by Shapeways in white plastic nylon. The piece is part of a series that investigates the concept of a plane peeling apart into checkerboard patterns, and the various possible interactions that can arise from it. Here, two strips lie in the same plane, one made from hollowed cubes, and the other from solid cubes, but instead of intersecting, they peel apart into checkerboards such that they arrange into two parallel planes that interlock perfectly without intersections. Inspirations for the work include the work of Bjarke Ingels and the M.C. Escher print "Two Intersecting Planes." --- Ari Smith

20 x 28 cm, StippleGen 2, MatLab, PowerPoint, 2016. This artwork was created with MatLab and Stipple Generator software with technical assistance from Dr. Timothy Chartier, Professor of Mathematics and Computer Science at Davidson College. The algorithm that Chartier's MatLab program used was based on the Traveling Salesperson Problem and is compatible with any digital image. I used the program to create this TSP art in memory of my former professor Dr. Reza Sarhangi (1952-2016), who was a Professor of Mathematics at Towson University, and he taught me while I pursued my undergraduate and graduate studies in secondary mathematics education. --- David Thompson

40 x 40 x 20 cm, ceramic and alpaca yarn, 2018. The idea behind this collaboration is to create unique and beautiful objects by combining ceramics and hyperbolic crochet. The ceramic portion of this sculpture is a surface known as a monkey saddle. The surface has negative Gaussian curvature at every point except the origin, which has zero curvature. The three lobes of the surface provide room for two legs and a tail. The hyperbolic crochet extends and exponentially increases the curve of the saddle. The many curls of the crochet provide seats for lots of smaller monkeys to sit with their tails on mom's saddle. --- Eve Torrence and Robert Fathauer

50 x 40 cm, print on metal, 2017. The Hopf map from the three sphere onto the two sphere induces a fibration of S^3 by circles. These circles can be used to create many beautiful symmetric patterns inside the three dimensional sphere, which we can then visualize under stereographic projection. This piece visualizes some of the circles arising from the preimage of a loxodromic curve on the sphere. --- Steve Trettel

17 x 17 cm, jade 25x25 cm Mulberry Paper, 2018. I was inspired to create a tessellation of my own, working off the basic square weave. This piece complicates a basic square weave by adding many more interwoven patterns and blowing up each vertex into a cycle of interwoven squares. This tessellation is different from some other origami tessellations in that it has an extremely nice back as well as front, containing cyclically overlapping squares at each corresponding intersection of weaves on the front. I thought it was amazing how a piece of folded flat paper was able to so aptly imitate a woven pattern. Although I went through many failures, the result was well. --- Aaron Yu



