
Mathematical ImageryMathematical artists create strong, stunning works in all media and explore the visualization of mathematics
The 2022 Mathematical Art Exhibition was held virtually during the Joint Mathematical Meetings in April. These are the recipients of the 2022 Mathematical Art Exhibition Awards: “Scherk Minimal Surfaces” by Laura Nica, awarded Best textile, sculpture, or other medium; “Septenary Circles” by David Reimann, awarded Best photograph, painting, or print; and “Is It Complete? Children's Solutions to The Hexagon Challenge” by Public Math and “Symmetric group on 4 Letters” by University of Kentucky Math Lab, co-Honorable Mentions.
The awards "for aesthetically pleasing works that combine mathematics and art" were established in 2008 through an endowment provided to the American Mathematical Society by an anonymous donor who wishes to acknowledge those whose works demonstrate the beauty and elegance of mathematics expressed in a visual art form.
View these and other works in various mediums submitted to the JMM 2022 Mathematical Art Exhibition.

Best Textile, Sculpture, or Other Medium
“Scherk Minimal Surfaces” by Laura Nica. 15x15x15 cm powder 3D print, 2015.
Nica is a digital designer and an architect. Her broader interests extend to material research, digital fabrication and simulation tools. Through parametric experiments and physical modelling, she analyses systems (either mathematical, biological, natural or structural), understanding the rules and testing out various parameters and spatial properties, which can then be scaled up to architectural or installation level. “In mathematics, a Scherk surface (named after Heinrich Scherk in 1834) is an example of a minimal surface. This is a surface that locally, minimizes its area (or having a mean curvature of zero). Initially an attempt to solve Gergonne’s problem, a boundary value problem in the cube, these surfaces arise from the solution to a differential equation that describes a minimal Monge patch (a patch that maps [u, v] to [u, v, f(u, v)]). The full surface is obtained by putting a large number the small units next to each other in a chessboard pattern.”

Best Photograph, Painting, or Print
“Septenary Circles” by David Reimann. 50 x 50 cm digital print, 2021.
“Through my art I make visible the beauty and wonder I see in the often abstract world of mathematics. I enjoy giving visual representations to mathematical concepts such as number, form, and process. I often use patterns that convey messages at multiple levels and scales using a wide variety of mathematical elements and media. Some of my work contains fine detail that allows the art to be viewed differently depending on the distance between the viewer and the art. Another prevalent theme in my work is symmetry, where the overall pattern is created by repeated rotation or translation of similar units. This artwork answers the question of how many ways can one place seven color pairs such that there is one other color between the first color pair, two colors between the second color pair, and so on. Mathematically, these are the twenty-six different Langford sequences corresponding to 7 colors. These sequences were first described by C. Dudley Langford in 1958 and popularized by Martin Gardner in 1967.”
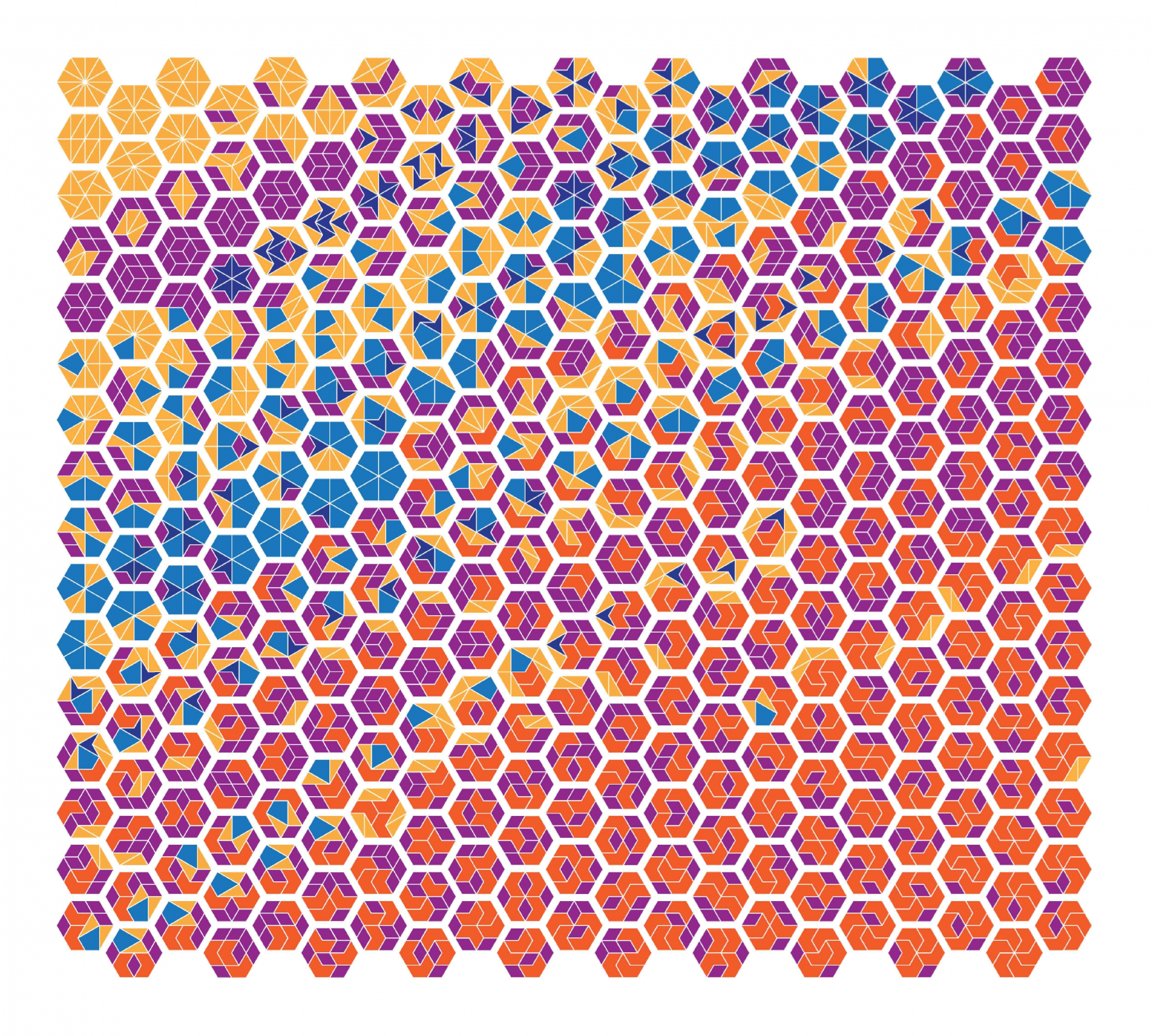
Co-Honorable Mention
“Is It Complete? Children's Solutions to The Hexagon Challenge” by Public Math. 70x50 cm digital print, 2021.
“Public Math supports positive math identities through projects that engage children, families, and adults in playful, creative mathematics as they go about their daily lives. We collaborate with teachers, parents, children, and others to upend harmful ideas about who does mathematics, what counts as mathematics, and the purposes to which mathematical thinking is put. An important theme engaged in this work is the relationship between playful, creative math and school math. The Hexagon Challenge consists of a set of colorful wooden polygons of five types and a hexagonal frame. The challenge is to fill the frame with the polygons and to find new arrangements. The original challenge was posed at the 2019 Minnesota State Fair, where children produced about 230 unique solutions which we captured with an instant camera and translated into a digital medium. In 2021, children expanded that solution set so that it now numbers 336. This artwork consists of a print showing all of these solutions, organized to be searchable and to encourage pattern seeking and noticing; it reports progress on an unsolved combinatorial geometry problem, and represents an attempt at proof by child or proof through play.”

Co-Honorable Mention
“Symmetric group on 4 Letters” by University of Kentucky Math Lab. 120x120x1 cm, fabric, thread, and cotton batting, 2020.
“The University of Kentucky Math Lab aims to encourage undergraduate math interest across a range of projects. These include research projects and outreach as well as visualization projects. We interpret visualization broadly making room for both 3d printing of polyhedra, simplicial complexes, and string diagrams and more traditional textile crafts such as quilting and crochet. This is a Cayley table for the symmetric group on four letters. Each element has a color and the colors are arranged to show subgroups and quotients. The 12 by 12 block consisting of the warm colored squares is the alternating group on four letters. The Klein four group is the 4 by 4 block of yellow squares. Both of these subgroups are normal. The top 2 by 2 square is cyclic of order 2 and not normal.”







