Archimedes' essay on the `Measurement of a circle' is often referred to but, I suspect, little read. What most modern writers are interested in is the prescription for approximating $\pi$ by considering polygons with a large number of sides, and the recursive recipe he developed to do this. This technique literally traveled around the world, and was the one used by everybody for calculating $\pi$ until the formula in terms of a series became well known. Archimedes' procedure is not exactly the same as he is usually quoted as presenting. The best account in modern terms that I am familiar with is in the book $\pi$ unleashed.
However, there are many subtle points about Archimedes' treatise that seem not to be widely appreciated. One of them is that his arithmetic is done in the awkward system common to the Greek world at that time, which incorporated what seems to us the bizarre way of dealing with fractions adopted from the Egyptians. Another reason his exposition is difficult to read is that he does not have algebra at his disposal. This has attracted a lot of comment, but the features I am going to discuss here are more fundamental mathematical matters.
The statement of Archimedes' Theorem
Archimedes' essay comes in two parts. The first is a statement and proof of a relationship between the area of a circle and its circumference. The second approximates $\pi$ by applying the techniques laid out in the proof of this first part. I shall be concerned with only the first although, as I say, it is the second that draws most attention.
In the version of `Measurement of the circle' that we now have, the opening statement is this:
| |
The area of any circle is equal to a right-angled triangle in which one of the sides about the right angle is equal to the radius, and the other to the circumference, of the circle. |
Roughly speaking, the reason the Theorem is true is that we can carve up both the circle and the triangle into very small regions that approximate each other closely in area:



The proof of this theorem in the extant version immediately follows its statement. I'll sketch it below, with a bit of explanation and a few more figures added. The basic idea is almost exactly the same as that of Euclid's proof of Theorem XII.2, which asserts that (in modern terms) the area of a circle is proportional to the square of its radius. In Euclid's proof the area of a circle is bounded above and below by the areas of circumscribed and inscribed polygons with an increasing number of sides, while in that of Archimedes the circumference is similarly also bounded. The overlap of Archimedes' argument with that of Euclid should not be surprising, since Euclid's Theorem XII.2 is an immediate consequence of Archimedes'.
The statement of the Theorem is itself interesting. In an algebraic formulation, we say that the area of a circle is $\pi r^{2}$ and its circumference is $2 \pi r$. These are consistent with Archimedes' claim: $$ \pi r^{2} = (1/2) \cdot r \cdot (2 \pi r) \, . $$ But the ancient Greeks did not have algebra, and they did not have the notion of a real number that we do. For Euclid, $\pi$ would not have made any sense, and in fact one of Archimedes' innovations was to come very close to the modern notion. Instead, they worked with ratios of quantities. Almost all their `formulas' are in the same style that this one is - they assert that two areas are equal. Thus they would not state that the area of a parallelogram is ${\rm base} \cdot {\rm height}$, but instead that a parallelogram has the same area as a rectangle with the same base and height.
Archimedes' argument has the same basic design as other arguments applying the method of exhaustion - carrying out some potentially infinite process until something happened to stop it. (The technique was Greek, but the term itself was coined in Europe hundreds of years later.) The discovery of this technique is implicitly attributed by Archimedes to Eudoxus, the only one of his predecessors he seems to respect. Eudoxus is elsewhere said to be the one who invented the extremely sophisticated way in which Euclid proved results about possibly irrational ratios. The method of exhaustion and the theory of ratios are the two most subtle parts of ancient Greek mathematics. They provided the touchstone of rigor in mathematics for several centuries, but applying them was an awkward business because it generally required a different approach to each problem. Still, there was no alternative until Cauchy in the early nineteenth century began the development of modern mathematical reasoning by introducing his algebra of inequalities.
The proof of Archimedes' Theorem
Let $C$ be a circle, $T$ be the triangle whose height is the radius of the circle and whose base is its circumference. The proof to come is in two parts, as are all the proofs by the method of exhaustion that i am familiar with. In the first it is shown that the area of $C$ cannot be greater than that of $T$, and in the second that it cannot be less. This leaves only the possibility that the two areas are the same
Part I. I am going to show first that the area of the circle is not greater than the area of $T$. We are going to need three facts in the argument to come, whose proof I postpone.
Claim (1) The area of any polygon inscribed in the circle is less than that of $C$.
Define inscribed polygons $\Pi_{4}$, $\Pi_{8}$, etc. by the condition that $\Pi_{4}$ be a square inscribed in $C$, $\Pi_{8}$ is the regular octagon constructed by dividing the arcs of $C$ in half along the sides of $\Pi_{4}$, and in general $\Pi_{2n}$ is the polygon with $2n$ sides obtained by dividing the arcs of $C$ in half along the sides of $\Pi_{n}$.

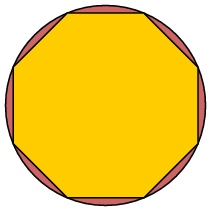

By (1) the area of $\Pi_{n}$ is less than that of $C$. Let $$ \delta_{n} = \hbox{ area of } C - \hbox{ area of } \Pi_{n} > 0 \, . $$
In the figures above, $\delta_{n}$ is shown as the red areas. Now comes
Claim (2): $\delta_{2n} < \delta_{n}/2$.
and
Claim (3) The area of any polygon inscribed in the circle is less than that of $T$.
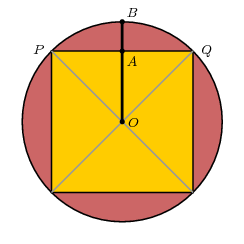
This is a bit more difficult to illustrate. Since both the polygon and the polygon $T$ can be partitioned nicely, in the following picture it follows from the claims that (a) the arc $PBQ$ is longer than the segment $PAQ$, and (b) the segment $OA$ is shorter than $OB$. The second follows from Euclid III.2, which asserts that the segment $PQ$ lies inside the circle. The first is evident in the picture, but we shall see later that there problems involved in believing what you see.

Now for the argument, assuming these claims to be true. Suppose, contrary to what we want to prove, that the area of $C$ is greater than that of $T$: $$ d = \hbox{ area of } C - \hbox{area of } T > 0\, . $$
It is a consequence of (2), according to the `Axiom of Archimedes' (which is actually Euclid X.1), we may choose $n$ large enough so that $\delta_{n} < d$ . We have now $$ \hbox{ area of } \Pi_{n} < \hbox{ area of } T < \hbox { area of } C \, , $$
which means that $$ d = \hbox { area of } C - \hbox{ area of } T < \hbox { area of } C - \hbox{ area of } \Pi_{n} \, , $$
a contradiction to the choice of $n$.
Part II. In the second half of the argument, we arrive at a contradiction by assuming the area of $C$ to be less than that of $T$, but this time by using circumscribed polygons. The only remaining possibility is that the area of $C$ is the same as the area of $T$, which is what we wanted to prove.
So in this part, let $\Pi_{4}$ be a square circumscribing the circle $C$, and in general let $\Pi_{2n}$ be the regular polygon of $2n$ sides obtained from $\Pi_{n}$ by cutting off half-arcs on $C$. In this case $\Pi_{2n}$ is strictly contained in $\Pi_{n}$, and contains $C$. Let $$ \delta_{n} = \hbox{ area of } \Pi_{n} - \hbox{ area of } C > 0 \, . $$



Again, it can be proved that $\delta_{2n} < \delta_{n}/2$. The replacement for claim (3) above is:
Claim (4) The area of $T$ is less than that of $\Pi_{n}$.
From here on the argument is very similar to that in Part I, deriving a contradiction from the assumption that the area of $C$ is less than that of $T$.
It remains to examine the claims (1) - (4). The simplest of all is (1). It follows directly from Common Notion 5 of Book I (`the whole is greater than its part') once know that a polygon constructed from segments cutting off arcs of a circle is contained in the circle. This is exactly what III.2 of Euclid asserts.
Claim (2) is the crucial part of Euclid's proof of X.2, which says that the areas of two circles is proportional to the squares of their radii. This is well explained in Heath's edition of Euclid's Elements, and I won't say any more about it. But claims (3) and (4) are definitely not in Euclid, and in fact together make one of Archimedes' great innovations. The problem is, how can one make sense of the length of a curve?
What exactly is the length of the circumference?
There is no place in Euclid where he talks about the length of anything but a line segment. We know now that this in fact potentially a very difficult matter, because there are continuous bounded curves in the plane that have infinite length. Of course the circumference of a circle is not one of these. The problem comes to this: how can one compare the lengths of two curves in the plane, or two surfaces in three dimensions? With areas in the plane the answer is relatively simple - one eventually arranges things so one area is contained in the other. But with curves this is not possible, so there is no really obvious answer to the question, ``In what circumstances can we tell easily whether one curve is longer or shorter than another?" How did Archimedes deal with the problem?
The problem arose first in what is perhaps the most famous work of Archimedes, On the sphere and cylinder I, in which he calculates the area of a sphere by comparing it to an enclosing cylinder. This is a more complicated notion that that of the length of the circumference of a circle, but it is similar. In the introduction to Sphere and cylinder he formulates two axioms that are exactly what he needs here, although he does not go into much detail, or justify his formulations. In a way this just dodges the difficulties, but at the same time it is very clever - it concentrates the difficulties in two relatively simple claims, in effect postponing them.
The first of Archimedes' axioms is the simplest comparison of curves possible.
Axiom 1. The line segment between two points is shorter than any other path between them.

The second is more subtle.
Axiom 2. Suppose two points $P$ and $Q$ to be given. Suppose two paths from $P$ to $Q$ are given, both of which are concave arcs on one side of the segment $PQ$. If one of them is contained inside the region bounded by the other and the line segment from $P$ to $Q$, it is the shorter.

A path from $P$ to $Q$ that lies on one side of $PQ$ is said to be concave if the region bounded by the path and the segment $PQ$ is convex. As far as I know, it was Archimedes who first used this in mathematics.
I am going to discuss these axioms in a moment, but first let me show how Claim (3) follows. In our original figure of triangle $T$ divided into small triangles, each of the smaller triangles has base equal to the length of the arc $PBQ$ in the following picture, while each height is $OP$. But by Axiom 1 the length of the arc $PBQ$ is greater than $PQ$, while it follows from Euclid III.2 that $OB$ is greater than $OA$. Applying symmetry, this implies Claim (3) in this case, and ought to suggest how the reasoning goes in general.
Axiom 2 is used in part II of the proof of Archimedes' Theorem.
Now we are left wondering, how did Archimedes convince himself of the Axioms above?
What justifies Archimedes' axioms?
To tell the truth, Archimedes gives nowhere, as far as I know, even the slightest hint of an answer to this question. But I am going to offer now some plausible reasoning that he might have used. First of all, as long as we are just looking for plausibility, we may simplify things to some extent by assuming that all the paths we are considering are polygonal ones.
Let's look at Axiom 1 first. In the simplest case, we are asserting that in a triangle the length of one side is less than the sum of the lengths of the other two sides. This is Euclid I.21, and forms the basis of the proof of the remaining cases, which proceeds by induction, which was familiar on an informal basis to Euclid. Suppose for example that we are given a polygonal path $P_{0}$, $P_{1}$, $P_{2}$, $P_{3} = Q$ of three segments from $P$ to $Q$. Draw the segment $P P_{2}$ and apply Euclid I.21: $$ PQ < PP_{2} + P_{2}Q < (PP_{1} + P_{1}P_{2}) + P_{2}Q \, . $$

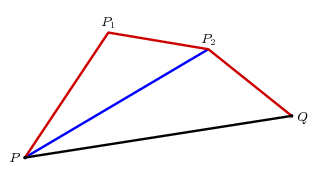

And so on, as Euclid might say.
Axiom 2 is more interesting. Again, look at a simple case, in which the inner curve was made up of two segments.
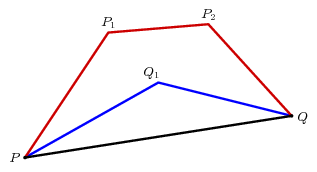
We want to know that the length of the inner path is less than that of the outer path: $$ PQ_{1} + Q_{1}Q < PP_{1} + P_{1}P_{2} + P_{2}Q \, . $$
The trick is to extend $PQ_{1}$ to $R$, the intersection of the line $PQ_{1}$ with the upper path. This point exists and is unique precisely because (a) the interior of the closed path $PP_{1}P_{2}QP$ is convex and (b) $PQ_{1}$ lies inside it.
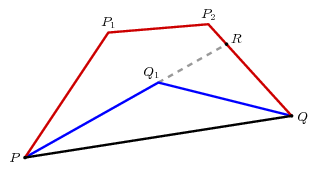
Applying Axiom 1 twice we get $$ \eqalign { PR &< PP_{1} + P_{1}P_{2} + P_{2}R \cr Q_{1}Q &< Q_{1}R + RQ \cr PQ_{1} + Q_{1}Q &< PQ_{1} + Q_{1}R + RQ \cr &= PR + RQ \cr &< PP_{1} + P_{1}P_{2} + P_{2}R + RQ\, . } $$
In general, we can apply induction on the number of segments in the inner path, as the figure on the left suggests:
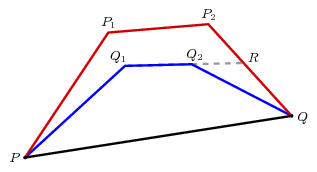

This works now because we have assumed the the inner path to be concave. This guarantees that the point $R$ lies on the top path $PP_{1}P_{2}Q$, which is where we want it. Whereas if the inner path wiggles around, this might fail, and the inner path might very well be longer, as the figure on the right demonstrates.
Where to read more
- Archimedes, Sphere and cylinder and Measurement of the circle, in T. L. Heath's translation of Archimedes' works. Published by Cambridge University Press in 1897, reprinted by Dover.
The version of the essay on the circle that was available to J. L. Heiberg (on whose Greek edition Heath based his translation) was somewhat disorganized. There is said to be a copy of this work in the Archimedes Codex now being edited (slowly) by Reviel Netz, but I do not know whether it is much different from what Heiberg and Heath had at hand.
The complete Heath edition can be found online at the Internet Archive. Links to this and other works of and about Archimedes can also be found at the New York University site Books on Archimedes.
- Jörg Arndt and Christoph Haenel, $\pi$ unleashed, Springer-Verlag, 2000.
- Judith Grabiner, The origins of Cauchy's rigorous calculus, MIT Press, 1981. Reprinted by Dover.
To most mathematicians, the use of $\varepsilon$ and $\delta$ in analysis is a second language, so well embedded into their ways of thought that it is hard to appreciate what a really marvelous tool the `algebra of inequalities' is. This book helps to recapture the original flavor of Cauchy's contribution.
-
Euclid, The Elements. Translated into English by T. L. Heath, originally published by Cambridge University Press, and reprinted by Dover.
This edition is valuable for its extensive commentary, although it is somewhat out of date. There is now available also a new and more literal translation into English by Richard Fitzpatrick, with English alongside Greek, and including a Greek-English lexicon.
-
Otto Toeplitz, The Calculus: a genetic approach, University of Chicago Press, 1963.
This book was produced from a fairly complete manuscript found after the author's death. It is a bit too eccentric for a practical calculus text, which is what the author seems to have intended, but it is highly original and often brilliant. Chapter I opens with a discussion of how the ancient Greeks dealt with infinite processes, and is one of the few places in the modern literature where one can find an intelligent discussion about how they thought of limits. It was from this book that I first learned about the method of exhaustion.
-
The Wikipedia entry on Madhava and the series for $\pi$ discovered by mathematicians from Kerala.
This part of the story is missing from the book by Arndt and Haenel.



 Bill Casselman
Bill Casselman




















