More ENIGMA
What I want to discuss in this feature is one part of Enigma operation that has been much written about elsewhere, but which still causes some confusion. This is the way in which key presses lead to rotor motion....
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
Email Bill Casselman
Introduction
An earlier Feature Column attempted to explain the mathematics behind the remarkable success of Polish mathematicians in breaking German Enigma codes during the years 1932-1939. I quote from the introduction to that previous column:
|
During World War II the British read German military communications regularly, because they were able to decipher messages encoded on the Enigma machines used by the Germans. As the war developed and the German networks became larger and more complicated, the methods used by the British became correspondingly more and more sophisticated, depending on a huge effort with thousands of people eventually involved in interception, decipherment, and interpretation of the German signals.
But the process started long before the war, in 1932, with a tiny group of Polish mathematicians. They made the first breaks into the Germans' code by relatively simple techniques that were fortunately able to deal with the relatively simple German encoding techniques of those early days.
One of the very first steps, and one of the most intriguing, was made by Marian Rejewski, who applied the theory of permutations in an interesting way to figure out `message keys' used by German operators as well as the structure of the German Enigma machines.
|
In that column I made an attempt to explain the mathematics I refer to, but in many ways that column was incomplete. I want to take up this subject again for several reasons. (1) In the past few years a number of valuable new sources (mostly Polish) have become available. Among them are two impressive accounts by Rejewski himself of his deciphering work, now translated from Polish into English. These are unfortunately published in a somewhat obscure Polish volume, and one of my aims here is to encourage someone to make it more accessible. In addition a Polish web site has links to many shorter memoirs by Rejewski that remain untranslated, and I hope to stimulate someone to translate them. (2) With the cooperation of the NSA I have taken a number of photographs of an Enigma machine that I want to use to discuss certain features of the machine that I believe the literature does not explain well.
Unfortunately, I have not enough space here to cover both these topics. So in this column I shall just deal with the second one, wishing for the moment just to call attention to the Polish literature and web site.
The Enigma machine
|

|
I first recall basic features of the Enigma machine.
It looks something like a rather complicated typewriter. In sending a message, an operator presses the successive keys of the message. When a key is pressed one of the lamps behind the key array lights up. A second operator records the letter that is lit, and when the entire message is recorded the encoded message (cipher text) is sent off by radio.
There are several components to the machine:
-
The keys
-
The plug board
-
The rotors
-
The lamps
At any given moment, the machine will translate keys pressed into lamps lit. This amounts to a simple substitution cipher (transformation from plain text to cipher text). When a key is pressed, it moves down. As it moves down it causes one or more of the rotors to rotate, and this changes the state of the machine so as to bring about a new substitution cipher. Finally, at the bottom of the key press an electrical contact is made, causing a lamp to be lit. As I shall explain (by a diagram) in a moment, the electrical circuit involves the plug board, three moving rotors, and a fixed 'rotor' that is not actually a rotor. The important point here is that the substitution implemented is that after the rotor motion, not the beginning.
|
|
Enigma machines were generally used for communication between headquarters and field units. Usage required three operators and a fair amount of equipment. A classic photograph recently made openly available by the Bundesarchiv shows the famous German Panzergeneral Guderian in a field vehicle with a team of Enigma operators. |

|
|
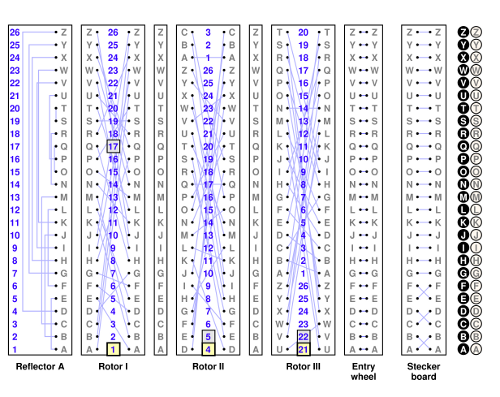
What follows is a schmatic diagram of the Enigma machine. In that diagram, the key pressed is A, and the lamp lit is B. The wiring is, as far as I have been able to figure out, the actual wiring of rotors used in reality. The Stecker board is what I also call the plug board. The Entry wheel is essentially fictitious--it is there to emphasize that the wiring connecting the plug board to the rotors is a matter of choice. In fact, figuring out this choice was not at all trivial, since the choices in the commercial and military machines were different. |
|

|
|
The most distinctive feature of the machine is that the subsitution corresponding to the 'rotor' at the left just swaps two letters: if A is changed to B then B is changed to A. Furthermore, no letter is ever taken to itself. In addition, the path of the circuit to this fixed rotor is just the reverse of the same as the path from it, which means that at any given moment the current substituon cipher also has these two properties. From the standpoint of the operators this is very convenient, since it means that the machine does not have to be configured differently for sending and receiving messages
However, as I tried to explain in the earlier column, this reversibility of the machine, compounded by a certain laziness in early Enigma usage, was the fatal flaw in the system that enabled the Polish success.
|
Comments?
Rotor motion
What I want to discuss in this feature is one part of Enigma operation that has been much written about elsewhere, but which still causes some confusion. This is the way in which key presses lead to rotor motion. There is one quirky feature involved.
First, I have to say something about the rotors. Just behind the lamps on the machine are three smal windows that display numbers in the range 1-26 corresponding to letters of the alphabet.

The cover with the windows in it can be lifted, and when this is done the rotors carrying the numbers become visible.

The correspondence between numbers and letters is the natural one, but--on this machine, at least--it is laid out on the inside of the wooden cover for the operator's convenience. (On some machines the display is in letters, not numbers.)

As the message proceeds, the numbers displayed are incremented. The right rotor is always incremented cyclically, going from 1 to 26 and then back to 1. When one rotor has advanced to a certain point the rotor on its left is also incremented. This is much like the odometer on a car, but because of the mechanism that implements this process, there are some slight differences.
How does a key press move the rotors? The keys are linked to three levers (called more precisely 'pawls') that are pushed out when a key is pressed. In each pair of images below you see first the pawls at rest, then pushed out.


Here is a closer look:


The pawls push against the rotors. On the right side of a rotor is a wheel with twenty-six notches, and on the other (at least in most models of Enigma) is a wheel with just one.


The right pawl moves out to the far right of the rotors, and the other two move out between the rotors to the left. The right pawl always engages the ratchet on the right-hand side of the right rotor and advances it. But what the other pawls do is a bit more complicated. First a view from the top, with the position of the extended pawls indicated:

Then a schematic side view of two neighboring rotors, with left unengaged, right engaged:

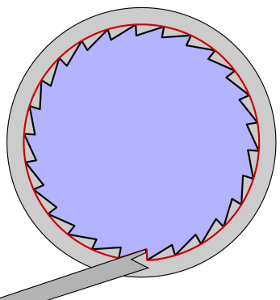
It should become clear from these pictures that when the pawl engages the right notch, the rotors to both its left neighbor and its right neighbor move. At the far right this makes no difference, since there is no right neighbor. Nor does this make any difference with the next pawl to the left, because the right rotor always rotates. But for the third pawl, it means that whenever the rotor at the left is moved, so too is the middle rotor. This is called double-stepping. Thus we get the following sequence of steps, in which the single notch is marked by the square outlined in gray:



In the next section I'll explore the consequences of double stepping.
Comments?
Maps and graphs
There are only a finite number of rotor positions, so as one enters a long message into an Enigma, sooner or later the state of the rotor must come back to some previous position. In this section I want to try to explain exactly how this works.
We have seen in the previous section that each rotor has on one side a single notch that determines when the rotor at its left advances. There are some complications that occur in reality, since the notch and numbers displayed are located on a ring that can be rotated relative to the internal wiring of the rotor. I am going to ignore this in the discussion to come. I am also going to number things $0-25$ instead of $1-26$.
Exactly where the notch is located relative to the numbers displayed depends on the particular type of rotor at hand. For example, in the rotor I in my diagrams the rotor advance takes place when 17 is visible. I am going to ignore this, too, and assume simply that the notch is activated when the number 25 is visible.
With these simplifying assumptions, we have these rules: (1) the right rotor always advances in each step; (2) if 25 is visible on a rotor, then in the next step both this rotor and the one to its left will advance. For example, we shall have the following sequence of visible triples:
25 25 25, 0 0 0, 0 0 1, 0 0 2, ...
and we ask: Will 25 25 25 ever recur? If not, what will be the first triple repeated? Which triples are in fact repeated? If the rotors behaved like a car odometer all triples would repeat and a triple repeats after exactly $26^3$ steps. With double stepping things are different. In the literature it is often asserted that the period of the rotor positions is $26 \times 25 \times 26$, but I am not aware of any place where this is justified. I shall do this here.
In understanding several features of the Enigma machine, it will help to have at hand a graphical description of an abstract construct. A map from any set to itself assigns to each element of the set another element of it. Thus the rules mentioned above define a map from triples of numbers in the range $[0, 25]$ to itself, mapping one rotor position to the next. There is a useful way to picture maps by what is called a graph, at least if the set is finite and small. The nodes of the graph are the elements of the set, and there is an edge from one element to another if the map takes the first to the second. It is not feasible to draw the graph defined by rotor advance, but it will be instructive to look at a simpler model.
Take the set to be that of all pairs $(x, y)$ with $x$, $y$ in $[0,2]$. The map follows these rules reminiscent of that defined by Enigma: (a) the value of $y$ always changes, incrementing by $1$ but cycling around to $0$ when $y=3$; (b) the value of $x$ increments similarly when $y = 2$, in which case both $x$ and $y$ increment. The set has 9 elements. Explicitly: $$ \eqalign { (0,0) &\mapsto (0,1) \cr (0,1) &\mapsto (0,2) \cr (0,2) &\mapsto (1,0) \cr (1,0) &\mapsto (1,1) \cr (1,1) &\mapsto (1,2) \cr (1,2) &\mapsto (2,0) \cr (2,0) &\mapsto (0,1) \cr (2,1) &\mapsto (0,2) \cr (2,2) &\mapsto (0,0) \cr } $$ and the corresponding graph is this:
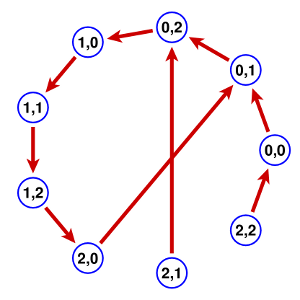
This can be summarized briefly by saying that after a few steps the system enters into a loop of $6 = 3 \times 2$ nodes. The states $(2,1)$, $(2,2)$, and $(0,0)$ can never repeat, but all other states can. Understanding this diagram should be a big step towards understanding how the (simplified) Enigma machine works. First of all one could look at the very similar map from $[0,25]^{2}$ to itself following the rules (a) the value of $y$ is always incremented ${\rm mod} \; 26$; (b) if $x = 25$ then both $x$ and $y$ are incremented. Part of the graph looks like this:

There is a loop of $25\times 26$, and another $26$ nodes feeding into it. The 26 ordered pairs $(0,0)$ and $(25,n), 1 \leq n \leq 25,$ are excluded from the loop. Similarly, and very roughly stated, in Enigma the chain $(m, 25, n)$ of length $26 \times 26$ is more or less excluded.
Where to learn more
-
Craig P. Bauer, Secret history: the story of cryptology , CRC Press, 2013.
Chapter 8 is on Enigma. This is useful, but weak on mathematical matters.
-
On the 100th anniversary of Maran Rejewski's birth, Perzeglad Historyczno-wojowsky, Warszawa, 2005.

This contains two very valuable memoirs by Rejewski in parallel Polish and English translation.
-
Marian Rejewski: living with the Enigma secret, published by the Bydgoszcz City Council, 2005.

A collection of essays, mostly in English, about Rejewski. Only 1500 copies were printed. Both this and the previous book are probably very difficult to obtain.
-
Jiri Tuma, Permutation groups and the solution of Enigma.
-
The English Wikipedia article on Rejewski.
As opposed to the earlier article, this seems to be essentially translated from the very complete Polish Wikipedia page.
-
A Polish collection of Enigma documents.
This includes particularly links to a number of Rejewski's Polish memoirs. It would be great to have English translations of them, or at least detailed English summaries.
-
Bill Casselman, Marian Rejewski and the First Break into Enigma (the first Feature Column on this topic).
Technical information about the machines
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
Email Bill Casselman



 Bill Casselman
Bill Casselman





















