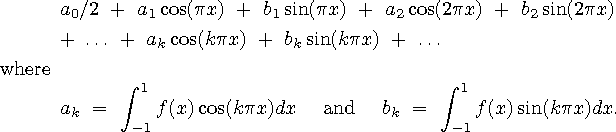Fourier Approximation Fourier Approximation
Fourier Approximation
1997 marks the 175-th anniversary of the publication, in 1822, of Joseph Fourier's Théorie analytique de la chaleur (The Analytical Theory of Heat), in which he advanced his idea of approximating functions on a closed interval, or, alternatively, periodic functions on the real line, by trigonometric polynomials. (He had been working on this idea since at least 1807.) For example, a function f(x) defined on the interval [-1,1] has a Fourier series (as we now call it)
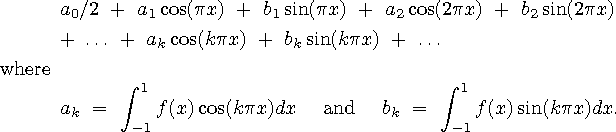
Since the time of Fourier, the question of convergence of Fourier series has been intensively studied.
Consider, for example, the function
f(x)=x(x2-1)(4x2-1)(9x2-4)(16x2-9) on the interval [-1,1].
This is an "odd" function, i.e., f(-x) = -f(x). For such a function, each ak = 0, so its Fourier series has only sine terms. The following images show the graphs of f(x) and some of its Fourier approximants. Here the n-th Fourier approximant sn(x) to f(x) is the sum of the first n terms of its Fourier series,


Graph of f(x) and its first, second, and third Fourier approximants.

Graph of
f(x) and its
fourth,
fifth, and
sixth Fourier approximants.
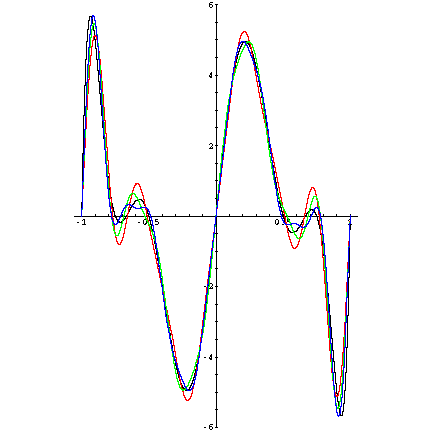
Graph of
f(x) and its
seventh,
eighth, and
ninth Fourier approximants.
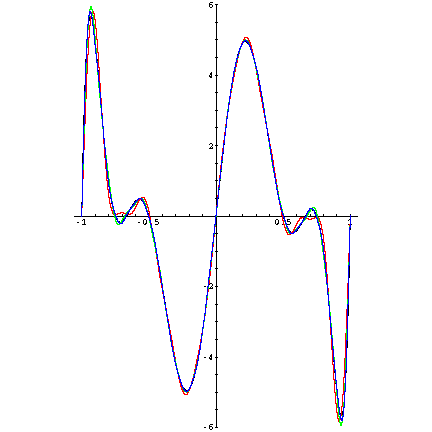
Graph of
f(x) and its
tenth,
fifteenth, and
twentieth Fourier approximants. (Note: To the resolution of this image,
f(x) and its twentieth Fourier approximant are indistinguishable.)
Here is a table of the first twenty Fourier coefficients of
f(x).
| k | bk | k | bk | k | bk | k | bk |
| 1 | 1.35174739 | 6 | .96466333 | 11 | -.22078270 | 16 | .07686692 |
| 2 | 3.17297840 | 7 | -.69694090 | 12 | .17369428 | 17 | -.06452967 |
| 3 | .51510823 | 8 | .50781673 | 13 | -.13886072 | 18 | .05467645 |
| 4 | 1.38915849 | 9 | -.37701467 | 14 | .11261631 | 19 | -.04671719 |
| 5 | -1.29334986 | 10 | .28569984 | 15 | -.09250886 | 20 | .04022103 |
- Steven Weintraub