Bin Packing

_{2. Basic ideas}

The bin packing problem asks for the minimum number k of identical bins of capacity C needed to store a finite collection of weights w₁, w₂, w₃, ... , w_n so that no bin has weights stored in it whose sum exceeds the bin's capacity. Traditionally the capacity C is chosen to be 1 and the weights are real numbers which lie between 0 and 1, but here, for convenience of exposition, I will consider the situation where C is a positive integer and the weights are positive integers which are less than the capacity.

Example 1:

Suppose we have bins of size 10. How few of them are required to store weights of size 3, 6, 2, 1, 5, 7, 2, 4, 1, 9?

The weights to be packed above have been presented in the form of a list L ordered from left to right. For the moment we will seek procedures (algorithms) for packing the bins that are "driven" by a given list L and a capacity size C for the bins. The goal of the procedures is to minimize the number of bins needed to store the weights.

A variety of simple ideas as to how to pack the bins suggest themselves. One of the simplest approaches is called Next Fit (NF). The idea behind this procedure is to open a bin and place the items into it in the order they appear in the list. If an item on the list will not fit into the open bin, we close this bin permanently and open a new one and continue packing the remaining items in the list. Of course, if some of the consecutive weights on the list exactly fill a bin, the bin is then closed and a new bin opened. When this procedure is applied to the list above we get the packing shown below. The bins are displayed here, and in the similar procedures we will develop later, from left to right. If you wish, you can think of the leftmost bin as being numbered 1, the next one 2, etc. The blue in the diagram is the amount of room in each bin which remains vacant or empty.

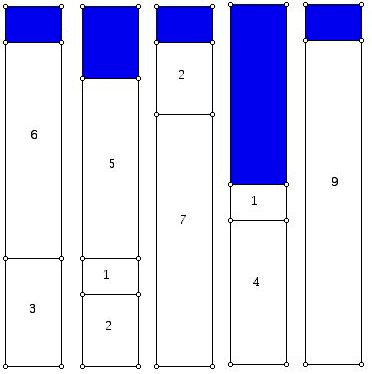
The appealing thing about Next Fit is that it is very simple and, in certain applied settings of the bin packing problem, it allows for bins to be shipped off quickly, because even if there is some extra room in a bin, we do not wait around in the hope that an item will come along later in the list which will fill this empty space. One can imagine having a fleet of trucks with a weight restriction (the capacity C) and one packs weights into the trucks. If the next weight can not be packed into the truck at the loading dock, this truck leaves and a new truck pulls into the dock. As Next Fit is carried out all that is required is that we keep track of how much room remains in the bin open at that moment. In terms of how much time is required to find the number of bins for n weights, one can answer the question using a procedure that takes a linear amount of time in the number of weights (n). Clearly, NF does not always produce an optimal packing for a given set of weights. You can verify this by finding a way to pack the weights in Example 1 into 4 bins. Procedures such as NF are sometimes referred to as heuristics or heuristic algorithms because although they were conceived as ways to solve a problem optimally, they do not always deliver an optimal solution. Can we find a way to improve on NF so as to design an algorithm which will always produce an optimal packing?

A natural thought would be that if we are willing to keep bins open in the hope that we will be able to fill empty space with items later in list L, we will typically use fewer bins. The simplest way to carry out this idea is known as First Fit. For First Fit, we place the next item in the list into the first bin which has not been completely filled (thought of as numbered from left to right) into which it will fit. When bins are filled completely they are closed and if an item will not fit into any currently open bin, a new bin is opened. The result of carrying out First Fit for the list in Example 1 and with bins of capacity 10 is shown below:

 

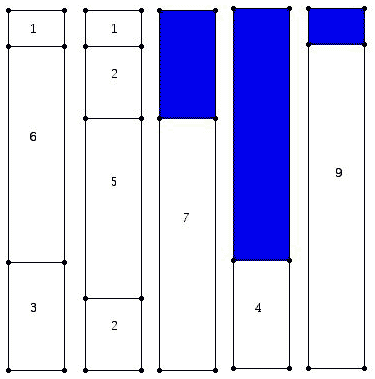
So far, both methods we have tried have yielded 5 bins. We know that this is not the best we can hope for. One simple insight is obtained by computing the total sum of the weights and dividing this number by the capacity of the bins. Since we are dealing with integers, the number of bins we need must be at least where . (Note that 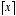denotes the smallest integer that is greater than or equal to x). Clearly, the number of bins must always be an integer. In Example 1, since 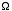is 40 and C is 10, we can conclude that there is hope of using only 4 bins. However, neither Next Fit nor First Fit achieves this value with the list given in Example 1. Perhaps we need a better procedure.

Two other simple methods in the spirit of Next Fit and First Fit have also been looked at. These are known as Best Fit (BF) and Worst Fit (WF). For Best Fit, one again keeps bins open even when the next item in the list will not fit in previously opened bins, in the hope that a later smaller item will fit. The criterion for placement is that we put the next item into the currently open bin (e.g. not yet full) which leaves the least room left over. (In the case of a tie we put the item in the lowest numbered bin as labeled from left to right.)

For Worst Fit, one places the item into that currently open bin into which it will fit with the most room left over. You should verify that Best Fit will give the same packing as the First Fit packing and Worst Fit packing the same as the Next Fit packing, though in general this will not always be true. Note that in Example 1, the fact that such a large weight item (weight 9) occurred as the last item in the list, was unforgiving in trying to use the given list to pack the items. In terms of tradeoffs with Next Fit, the amount of time necessary to find the minimum number of bins using either FF, WF or BF is higher than for NF. What is involved here is n log n implementation time in terms of the number n of weights.

To make sure that you follow the distinction between First Fit, Best Fit and Worst Fit, suppose that we currently have only three bins open which have capacity 10 and have remaining space as follows: Bin 4, 4 units, Bin 6, 7 units, and Bin 9 with 3 units. Suppose the next item in the list has size 2. First Fit puts this item in Bin 4, Best Fit puts it in Bin 9, and Worst Fit puts it in Bin 6!

Returning to Example 1, perhaps one difficulty is that we are applying "good procedures" but on a "lousy" list. If we know all the weights to be packed in advance, is there a way of constructing a good list? We will return to this shortly.

Bin packing is a very appealing mathematical model, and yet work on this problem is surprisingly recent. As an organized subject this topic is only about 35 years old. Major pioneers and contributors in working on this problem are Edward Coffman, Jr., Michael Garey, Ronald Graham, and David Johnson.
 

Edward Coffman, Jr.



Michael Garey




Ronald Graham





David Johnson
 

Interestingly, at various times in their careers all of these men worked in the communications industry, typically as researchers in a think-tank environment. They have not only excelled as scholars but as administrators and group leaders of research teams.

1. Introduction
2. Basic ideas
3. More approaches to bin packing
4. Applications of bin packing
5. References