From Euclid to public-key codes

Mopping up: How do you calculate the private key, and what makes it work?

The number k was chosen to be relatively prime to (p - 1)(q - 1). In Book VII of the Elements (Proposition 1 and Proposition 2) Euclid gives a process which we now call the Euclidean Algorithm. This process, essentially repeated long division, can be used (The Extended Euclidean Algorithm) to produce the numbers s and t which enter into the following very useful fact:

• If two integers m and n are relatively prime, then there exist integers s and t such that
  

  For example, for 65 and 18 the Euclidean Algorithm produces s = 5 and t = 18:

  

Applying this algorithm to the numbers k and (p - 1)(q - 1) gives numbers s and t with

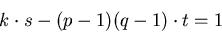
or

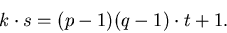
This is how the secret key s is calculated. This number is the mod (p - 1)(q - 1) multiplicative inverse of k since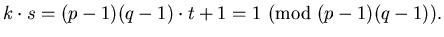

To understand why s undoes k, i.e., why 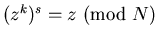, it helps to know about the Euler phi-function.

• The Euler phi-function assigns to an integer n the number of numbers less than n and relatively prime to n. (The number 1 is counted!) The number s is written (n). Since 11 is prime, all the numbers less than 11 are relatively prime to 11, so (11) = 10, and similarly (p) = p - 1 for any prime p. The only numbers less than 12 which are relatively prime to 12 are 1, 5, 7, and 11, so (12) = 4.
• If 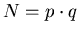with p and q prime numbers, then (N) = (p - 1)(q - 1).
  This can be checked by counting the number of numbers less than N which have a factor in common with N.

The importance of (N) here is:

• Euler's Theorem : For any integers z and N which are relatively prime,

Now the calculation can be finished using this theorem and (N) = (p - 1)(q - 1):

Back to the previous codes page.

Back to the first codes page.

Search Feature Column