Feature Column from the AMS

Digital Revolution (II) - Compression Codes and Technologies

Huffman codes

5. Huffman codes

In principle Huffman codes can be used for a wide variety of compression tasks, but as progress has been made in the theory and practice of compression technology, newer approaches to compression have supplanted their use. However, the mathematical ideas behind Huffman codes remain as fresh and exciting as when they were first developed. Huffman developed his ideas at MIT where he was working under the supervision of Robert Fano.

David Huffman

Imagine that we have a text or image. For a text assume we know in advance exactly how many times each character (i.e. lower case or upper case letter, space, punctuation symbol) appears. In the case of an image, we would assume that the gray levels of the pixels in the image are all known in advance. In either case we know the relative frequencies (probabilities) of the items that we must develop a compression code for. The algorithm for constructing a Huffman code to represent items with given relative frequencies (probabilities) of occurrence proceeds in two phases. First, one constructs a Huffman tree based on the relative frequencies. Second, using the Huffman tree, one constructs the code words that go with the given relative frequencies. A simple example will illustrate the lovely ideas involved.

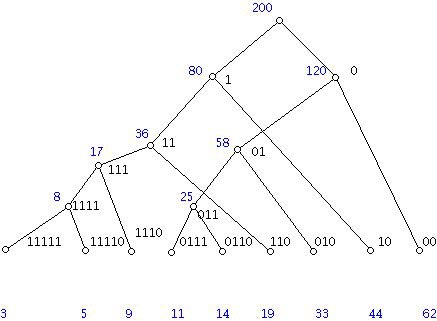
Suppose that one needs a code to represent nine types of information that occur with given relative frequencies, 3, 5, 9, 11, 14, 19, 33, 44, and 62. (There are 200 items to represent.) One can think of these items as nine different gray levels that occur in a certain family of medical images. In realistic examples the number of gray levels would, of course, be much larger. One begins with assigning a vertex of a tree for each item, labeled so that the relative frequencies increase from left to right. We construct a tree by adding a new vertex to the previously existing construction by selecting the two vertices, v and w, in the current structure with the smallest labels (in case of a tie, pick any two) and adding a new vertex to the structure with a label which is the sum of the labels at v and w. Place this new vertex above and between the two vertices v and w. In the diagram shown the original frequencies start at the bottom and the new levels are shown in blue.

A Huffman tree and associated Huffman code

This tree is now used to construct the code words associated with the nine different gray levels. One labels the top vertex of the tree (the root) with a blank string. As one moves down the tree, one labels the next vertex one gets to with a binary string by appending a 0 or 1 to the right according to whether one moves to the next vertex by taking a right branch or a left branch. For example, the vertex with the blue label 58 has the string 01 associated with it. The vertex to the right and below this is labeled with 010, and the vertex to the left and below it is labeled 011.

This process will wind up assigning short code words to gray levels which occur frequently and long code words to gray levels which rarely occur. We can be more precise about this. For each code word we can compute how many levels we must go up to get to the top (root) of the tree. We can weight the number of times this code word is used by the number of levels we must go up. Of course, this number is also the length of the code word.

Here is the computation for the example we did above:

2(62) + 2(44) + 3(33) + 3 (19) + 4(14) + 4(11) + 4(9) + 5(5) + 5(3) = 544.

Since there are 200 gray levels to code, the Huffman code just constructed will need 544/200 = 2.72 binary bits per gray level to do the encoding. This compares with 200(4) = 800 bits if compression were not used. (200 gray levels at 4 bits per gray level would require 800 bits compared with 544 using the Huffman code.)

As you can see, Huffman's idea is very simple and very clever but it does mean that one must know in advance the relative frequencies to put it to use. Clever adaptations of Huffman's method known as dynamic Huffman codes or adaptive Huffman codes were subsequently developed to overcome this problem. However, as it became increasingly clear how important compression was to new digital technologies, a flood of new compression methods were developed.