| In this analysis we take the radius of the wheel to be 1. We consider the equilibrium configuration with the wheel in vertical position and the second elastic (not shown in the diagram) stretched down so as to exactly compensate the pull of the first. Since these are identical elastics, with the same spring constant k, they will each have been stretched a distance L from their rest length, and each will be pulling with a force equal to kL. An exactly similar analysis will apply to the position where the roles of the two elastics are reversed. We will apply approximations which are useful for small angles 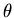 . . When the catastrophe machine is turned through an angle 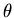 from its (vertical) equilibrium point, the restoring torque is due to the stretch of the two elastics. Elastic number one has been stretched by an amount which is approximately the purple length in the diagram, i.e. from its (vertical) equilibrium point, the restoring torque is due to the stretch of the two elastics. Elastic number one has been stretched by an amount which is approximately the purple length in the diagram, i.e.  , so the force it exerts has been increased to k(L+ , so the force it exerts has been increased to k(L+ ); the length of the other elastic has been diminished by the same amount, so it is pulling down with force k(L-( ); the length of the other elastic has been diminished by the same amount, so it is pulling down with force k(L-( )). To a first approximation the angle between the two elastics is flat enough, for small )). To a first approximation the angle between the two elastics is flat enough, for small 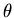 , so that the forces can simply be subtracted, leaving a restoring force (blue arrow) directly proportional to , so that the forces can simply be subtracted, leaving a restoring force (blue arrow) directly proportional to  . The restoring torque (red arrow) is the tangential component of this force: examination of the diagram shows that this component is equal to the magnitude of the force multiplied by . The restoring torque (red arrow) is the tangential component of this force: examination of the diagram shows that this component is equal to the magnitude of the force multiplied by  . The restoring torque . The restoring torque 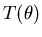 is thus proportional to is thus proportional to 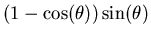 , which is well approximated by , which is well approximated by 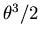 for small values of for small values of 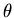 . So the restoring potential, which is calculated by integrating . So the restoring potential, which is calculated by integrating 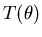 with respect to with respect to 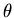 , comes out proportional to , comes out proportional to  . . |  |



