Descartes 5Descartes's Lost Theorem
Descartes's curvatura
Euler's Theorem is equivalent to Descartes's Lost Theorem, but the methods by which they arrived at their results must have been quite different. In fact Descartes's Theorem appears in his work as a consequence of an observation for which there is no parallel in Euler.
Descartes defines the exterior solid angle ata vertex of a polyhedron as ``that quantity by which the sumof all the plane angles which make up the solid angle is lessthan four plane right angles'', i.e., 2 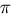 minusthe sum of the face angles at that vertex, and he states:
minusthe sum of the face angles at that vertex, and he states:
Just as in a polygon the sum of the exterior angles is equal to four right angles, so in a polyhedron the sum ofthe exterior solid angles is equal to8 solid right angles.
Descartes does not have a completely coherent definitionof what a solid right angle should be, and this may be one reason why he never published his Treatise.But computationally he interpreted his statement asmeaning:
(Sum of exterior solid angles) = 4 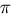 ,
,
and in this form it is clearly equivalent to his LostTheorem.
Descartes expands on his definition of exterior angle: ``By exterior angle I mean the curvature and slopeof the planes with respect to each other... .'' In hisuse of curvatura he foreshadows by two centuries Gauss's definition of the intrinsiccurvature of a surface.
On to next Descartes page.
Back to previous Descartes page.
Back to first Descartes page.
Welcome to the
Feature Column!
These web essays are designed for those who have already discovered the joys of mathematics as well as for those who may be uncomfortable with mathematics.
Read more . . .
Feature Column at a glance



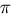 minusthe sum of the face angles at that vertex, and he states:
minusthe sum of the face angles at that vertex, and he states: