|
He was 40 years old before he looked in on Geometry; which happened accidentally. Being in a Gentleman's Library, Euclid's Elements lay open, and 'twas the 47 El. libri I. He read the Proposition. By God, sayd he (he would now and then swear an emphaticall Oath by way of emphasis) this is impossible! So he reads the Demonstration of it, which referred him back to such a Proposition; which proposition he read. That referred him back to another, which he also read. Et sic deinceps that at last he was demonstratively convinced of that trueth. This made him in love with Geometry.
From the life of Thomas Hobbes in John Aubrey's Brief Lives, about 1694. Proposition I.47 is Pythagoras' Theorem, and "Et sic deinceps" can be translated "going thus one after another".
|
Euclid's Elements of Geometry has been one of the most popular books ever written, appealing over more than 2,000 years to people of all major civilizations, but recently it has ceased to be read much, even by mathematicians. This is unfortunate, since if interpreted carefully it is perhaps still the best place to learn what a mathematical proof---indeed, mathematics---is like.
Its reputation among mathematicians has probably suffered from the penetrating analysis of plane geometry by David Hilbert at the end of the nineteenth century. Hilbert wrote at the end of a long period of exploration of the nature of axiom systems that started with the discovery of non-Euclidean geometry towards the beginning of the century. With this discovery it became apparent that Euclid's geometry no longer described the logically necessary description of reality that it had appeared to be, but an idealization of a possibly very complicated universe. It had also become apparent to mathematicians that certain features of Euclid's system were lacking in rigour at even a very low level---its foundations were shaky. Most notable was his failure to be careful about notions of order on a line. Hilbert himself rebuilt the foundations and devised a perfectly rigourous account of plane geometry in his book Grundlagen der Geometrie (translated as Foundations of Geometry), which showed up but also fixed definite logical flaws in Euclid's system.
However, the subsequent abandonment of Euclid as an educational tool is almost certainly not what Hilbert intended. After Hilbert, nobody can look at Euclid and say, here is a perfect example of rigourous deduction, but neither can one deny the skill with which Euclid did proceed in building an attractive logical basis of geometry step by step. It is no longer feasible to think of the Elements as perfect logic, but one can still see it as a way to deduce complicated phenomena from simpler ones---very complicated ones from much simpler ones, in fact. Of course one can choose other parts of mathematics to use as a model of mathematical deduction, but geometry has a definite attraction, even if it is a flawed model. Humans like pictures.
In this column I want to give some idea of how subtle Euclid can be by tracing the reasoning involved in proving the last major assertion of the Elements, that there are no more than five regular polyhedra. This is by no means the most complicated thing done by Euclid, but it is one of the most interesting.
There are thirteen books in the Elements. Much of Books XI, XII, and XIII is concerned with the geometry of three dimensions, and nearly all of the last one is concerned with the regular polyhedra. Most of it is spent showing how to construct them, and how to prove that the figures constructed do possess the symmetry required. This is not at all a trivial pursuit, but I'll say no more about it. What I want to discuss is the very last part of the treatment of the regular polyhedra, which reads in Heath's English translation:
|
I say next that no other figure, besides the said five figures, can be constructed which is contained by equilateral and equiangular figures equal to one another.
|
There are several curious things about this assertion. First of all, it is not declared to be a Proposition, and is not given a number. I am going to call it Proposition XIII.19, because it comes after XIII.18, but that is just for convenience. There are also other, more technical, ways in which it is not in Euclid's usual formal style. In some accounts it is referred to as a postscript, and indeed that's what it looks like. There must be some interesting story attached to it. There are many other Propositions in Euclid whose only point seems to be in proving this assertion, so one unavoidably imagines that Euclid certainly had it in mind. Why did he not include it in his ordinary style? Was this inclusion not written by him? Did he die before completing Book 13? If it is not due to him in one way or another, when and by whom was it added? Did Euclid leave notes to indicate what he expected to add? We shall almost certainly never know the answers to any of these questions. But then what don't we really know about even the simplest aspects of Euclid's life is vastly greater than what we do know.
A second is that the assertion is a bit hard to interpret, and on one reading false, as I'll explain in the next section.
A third curious thing is that its proof is much less formal than the usual proofs in the Elements---it is really not much more than a few casual remarks, with inadequate references to earlier and apparently necessary Propositions in the Elements.
A fourth is that while the proof is essentially correct, at least in one interpretation, it is not quite complete. I'll say something about that in a moment.
What is a regular polyhedron?
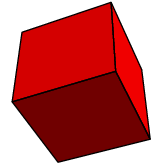
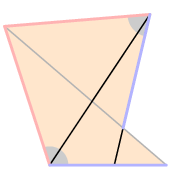
The first problem is to understand exactly what Euclid's assertions mean. Is the following figure contained by equilateral and equiangular figures?
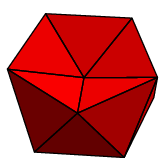
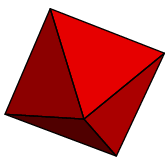
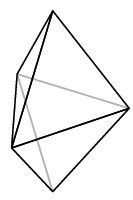
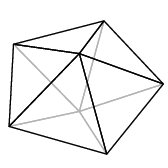
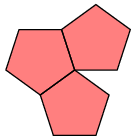
As occasionally occurs elsewhere in the Elements, there is an implicit assumption involved---here, that the figure is convex. I'll not recall the precise definition, but what it means in rough terms is that the figure bulges out everywhere. Granting this, a regular polyhedron to Euclid would apparently mean a convex three-dimensional figure all of whose faces are congruent copies of one two-dimensional regular polygon. But if this is the definition, the assertion is still false, since we can assemble many figures out of equilateral triangles that we would not consider regular. Here are a couple:
What's wrong with these is that the face count around vertices is not always the same---some vertices have three triangles meeting there, while some have four. So we add the condition: around each vertex the same number of faces meet. Is this perhaps included in the Elements' specification of equiangular? My knowledge of mathematical terminology of classical Greek is not good enough to decide.
But now a new problem arises---it is true that there are only five regular polyhedra in this sense, but as far as I can tell this wasn't proved until the early nineteenth century, and by techniques alien to Euclid. The problem is that the vertices are not completely determined by specifying the number or type of faces meeting at it---such vertices are not rigid. This is because polygons with more than three sides are not rigid. However, Cauchy, in about 1813, showed that this local flexibility does not lead to a global one, at least for convex solids.
Euclid (or whoever wrote our XIII.19) can still be redeemed, however, by specifying that the vertices as well as the faces possess rotational symmetry. I summarize, in terms that would be more or less familiar to Euclid:
|
A regular polyhedron is a convex solid whose faces are all copies of the same regular two-dimensional polygon, and whose vertices are all copies of the same regular solid angle.
|
This is the notion of regular polyhedron for which Euclid's proof of XIII.19 is essentially valid, although it is still somewhat incomplete.
What Euclid does and doesn't prove
What Euclid deals with entirely successfully, and what we shall look at in detail, is what can happen at a single vertex. What he does not deal with is how what happens at one vertex determines what happens overall---he (perhaps I should say "he") simply doesn't raise the question. I find this striking. Given the definition of a regular polyhedron that we have agreed on, it is possible to complete the proof in elementary terms, but it is not entirely clear to me that it can be completed in terms that would be familiar to Euclid. One might speculate that if what I call XIII.19 was not put in the Elements by Euclid, it is because he had some problem in completing his proof. It frequently occurs even in modern times that a mathematician launches himself on a project only to realize only near the end that the original idea is not quite adequate to the task at hand.
The Elements has many virtues if used as an introductory text in mathematics. It is not, as I have already said, perfectly rigourous, but it does succeed in reducing complicated theorems to simpler ones. That it succeeds in this is not independent of its lack of rigour---the things that he doesn't get quite right are those that seem entirely obvious. In other words, he fails precisely because our strong geometric intuition deceives us into seeing and accepting logic that isn't there. Mathematicians have been aware of this source of deception for a long time---roughly from the beginning of modern analysis in the seventeenth century. It has continued to be a problem well into modern times, for example in several false proofs of the Poincaré conjecture that came before Perlman's correct proof, or in a recent false proof of the well known conjecture of Johannes Kepler that came only a few years before the correct one found by Tom Hales.
The most famous statement about these dangers is found in the preface to Lagrange's Méchanique analitique of 1787, where we find: One will find in this work no diagrams. The methods that I use require no constructions, no geometrical or mechanical arguments, but only algebraic operations, subject to a regular and uniform process..

Or, from a much more recent source: ... this technologically driven evolution away from `logocentrism' often associated with modernity and progress ... projects us into dangerously archaic states of collective consciousness. (Yuri Manin in The notion of dimension in geometry and algebra.)
My own view of this is that sure, in the end mathematical proofs must be ... uhhh ... logocentric. But in my own experience, for every person competent at following close verbal reasoning there are at least half dozen or so who are capable of following visual reasoning quite happily in order to get the basic idea if not the details. This seems to be very little acknowledged by mathematicians---maybe because they are, after all, the survivors in the current game.
I'll not say more about Euclid's lack of rigour or the local/global problem. What I want to do is discuss now is what can be found in the Elements, rather than what cannot.
Reduction to Proposition XI.21
Throughout the Elements, Euclid is careful to refer only to results already proved. Remarkably, and inadequately, the proof of XIII.19 to be found there refers only to Proposition XI.21, which says that the sum of angles around a convex solid angle is less than $360^{\circ}$. Let's first see why that's basically sufficient.
Proposition. (Euclid XI.21) The sum of angles around the vertex of any solid angle is less than $360^{\circ}$.
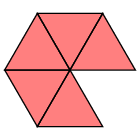
A less formal way to phrase this is that if we flatten out a vertex of a convex solid angle, we get a gap. That is certainly true of the regular polyhedra, for which we get the following figures:
But what Euclid doesn't do is go into the details necessary to restrict the splayed vertices of regular polyhedra to this list, by telling us what the interior angles of the triangle ($60^{\circ}$), the square ($90^{\circ}$), and the pentagon ($108^{\circ}$) are. It's an easy gap to fill, but this is just one more bit of evidence of the sloppiness that has gone into XIII.19 as we now have it.
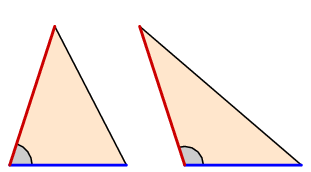
Let's look now at the proof of XI.21. I should remark right away that perhaps the most satisfactory proof was discovered by Descartes, around 1630. Descartes tells us what the difference between $360^{\circ}$ and the sum of vertex angles is, which he calls the defect, in terms of the area of a certain polygon on the sphere. In other words he gives an attractive interpretation of the defect. This was one of the very first genuinely new theorems in geometry discovered by European mathematicians in the century just after the Renaissance had introduced Europe to Greek mathematics. I ought to say also that there is a trap lurking in this business. If one thinks that the Proposition is obvious, it is probably because he has in mind the following picture:
This picture suggests that perpendicular projection always shrinks angles, but that is not easy to prove (I leave as exercise: is it false?), and in any event the techniques of vector calculation we would use were not available to Euclid.
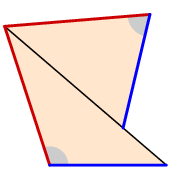
Given these difficulties, Euclid's proof is admirable. He deftly transforms the problem into another, very different one, of great independent interest. First of all, just for convenience of notation, I assume the vertex is tetrahedral (I am in good company, since Euclid does the same):
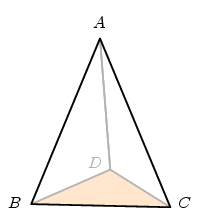
The angles we are summing are those at $A$ in the three triangles around it. I need some notation to describe what's going to happen. Basically, we label the vertices of a pyramid at the vertex, $A$ as the vertex itself, and triangle $BCD$ at the base. Refinements are best explained by unfolding the vertex along one of the edges, here $AD$, and flattening out our pyramid:
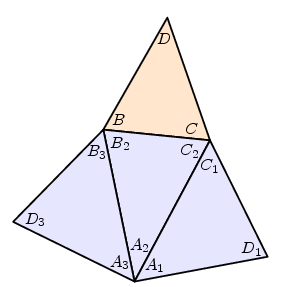
What we want to show is that $A_{1}+A_{2}+A_{3} < 360^{\circ}$. What we know is that the sum of all the angles of the three triangles neighbouring triangles is $$ 3 \cdot 180^{\circ} = (A_{1} + A_{2} + A_{3}) + (B_{2} + B_{3}) + (C_{2}+C_{1}) + (D_{1}+D_{3}) . $$ In a moment I am going to prove that $$ (B_{2}+B_{3}) > B, \quad (C_{2}+C_{1}) > C, \quad (D_{1}+D_{3}) > D \, , $$ which I'll call the angle inequalities. Since $B+C+D = 180^{\circ}$, these lead to $$ 3\cdot 180^{\circ} > (A_{1} + A_{2} + A_{3}) - (B+C+D), \quad A_{1}+A_{2}+A_{3} < 360^{\circ} . $$ But why on Earth do the angle inequalities hold? I'll give the proof in a moment, but first I'll explain why the Proposition is intuitively believable.
Geometry on a sphere
The trios of angles in the angle inequalities are not arbitrary, they are angles at the center of a solid angle. For these we have
Proposition. (Euclid XI.20) If $\alpha$, $\beta$, $\gamma$ are any angles at a trihedral vertex in three dimensions, then $\alpha < \beta+\gamma$.
I have to explain what this means. We are given a vertex, which I may take to be the origin, and a trihedral cone radiating out from it:

One of the angles of the planar regions meeting at the vertex is proportional to the length of the great circle cut out by the regions on the unit sphere. So what the inequality of XI.20 amounts to is that the arc length of one side of a spherical triangle is less than the sum of the arc lengths of the other sides. As far as I know, Euclid did not see it that way, but later Alexandrian mathematicians did make such a formulation. Menelaus, in fact, wrote an entire work devoted to proving spherical analogues of the elementary results about plane geometry. But then, who really knows how Euclid really saw things in his mind's eye? He never tells us.
The proof of XI.20
I follow Euclid.
For any given trihedral vertex, there is only one case for which the proof is not trivial, that in which the angle $\alpha$ is longer than $\beta$ and $\gamma$. Slice the solid angle to get a pyramid with vertex $V$ and base $ABC$ such that angle $ACV = BCV = \theta$.
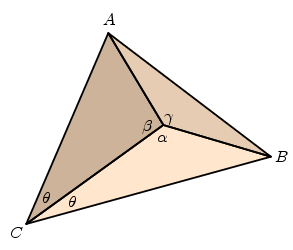
This allows us to make a copy of the triangle $ACV$ inside the triangle $BCV$. Let $A'$ be the image of $A$ in this copy.
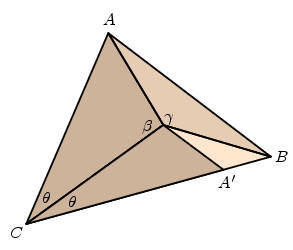
Because of the ordinary triangle inequality (Euclid's I.20) we have $CB < CA + AB$. But $CB = CA' + A'B$ and $CA' = CA$, so $A'C < AB$. We now consider the triangles $ABV$ and $A'BV$. They have two sides of equal lengths. Proposition I.25 of the Elements tells us that the angle $A'VB$ is less than $AVB$, and adding ip $$ \alpha = CVB = CVA' + A'VB < CVA + AVB = \beta + \gamma $$
What we need from Book 1
Given what we have seen in the previous section, it should not be a surprise that one of the main ingredients of Euclid's proof of XI.20 is the ordinary triangle inequality. But there are some others worthy of mention:
Proposition. (Euclid I.32) In any triangle, the exterior angle of one corner is equal to the sum of the opposite interior angles.
This is equivalent to saying, the sum of the interior angles is $180^{\circ}$. It's used in several places above.
Proposition. (Euclid I.25) Given two triangles with pairs of matching sides, the one with the longer third side has the larger angle opposite that side.
As far as I know, the only place where this is used is in the proof of XI.20. If the matching sides all have the same length, it is an immediate consequence of what we now know as the cosine rule of triangles, but of course Euclid did not have this at his disposal.
This is the only one of these results from Book I that I prove here, because my favourite proof is not Euclid's, but the one found later by Menelaus (and presented in Heath's supplementary note in this Proposition).
Here is Menelaus' proof. I tell the story in pictures.
For the last step, we need to know that in an isosceles triangle, matching sides have matching opposite angles (Euclid I.5, attributed to Thales, whom tradition calls the founder of Greek geometry), and also Proposition I.18, which I quote below.
Proposition. (Euclid I.20) In any triangle, the length of one side is less than the sum of the lengths of the other two sides.
This is the two-dimensional triangle inequality.
Proposition. (Euclid I.18) In any triangle, the angle opposite a larger side is larger.
Final remarks
Reading Euclid is at first sight a daunting prospect. But you get better at it as you go on. One thing you realize very quickly is that in the proof almost every Proposition there is some crucial point upon which the whole proof is based. People like puzzles, and figuring out this point is like solving a very intriguing puzzle. Learning how to do this is an extremely valuable exercise.
Another thing to keep in mind is that going through Euclid step by step, Proposition after Proposition, is a very bad idea. Mind numbing. For example, I.25 all by itself seems almost pointless. So the best way to read Euclid is to start with something interesting and trace backwards to see how the proof is built up.
Where to read more
- P. Cromwell, Polyhedra, Cambridge University Press, 1997.
Chapter 6 is about Cauchy's theorem. Descartes analysis of the defect of vertex angles is in Chapter 5.
- Euclid, The Elements of Geometry.
The Dover edition is in three inexpensive volumes, and well worth buying. This translation and the accompanying comments have been much criticized by specialists in the history of mathematics, but for most of us these criticisms are irrelevant.
The complete text of Heath's translation can be found at David Joyce's web site. Here, more particularly, is Book 13.
One nice feature of this site is the ability to interactively trace links in Euclid to previous and subsequent results. There is also a convenient guide to the logic, added by Joyce. One thing missing from Joyce's pages are the comments by Heath, which are extremely variable. They used to be available elsewhere on the Internet, but no longer seem to be. This is a shame---the comments provide useful cribs to Euclid's reasoning as well as alternative proofs contributed down through two thousand years, and a very readable if somewhat outdated history of the book and the cultures that read it.
- R. Hartshorne, Geometry: Euclid and beyond, Springer-Verlag, 2000.
Chapter 8 deals with polyhedra, and explains well at what point Cauchy's rigidity theorem is required for one version of the uniqueness of regular polyhedra.
- David Hilbert, The Foundations of Geometry, Open Court Publishing Company.
This has appeared in several English editions translated from successive German editions of Grundlagen der Geometrie. If you like to read Euclid, you'll probably enjoy reading Hilbert as well.
- Yuri Manin, The notion of dimension in geometry and algebra, in the Bulletin of the American Mathematical Society 43 (2006), no. 2.
There are some interesting comments about this article on the Internet, for example Peter Woit's.
- Tony Phillips' Feature Column on Descartes' Theorem.
Bill Casselman
University of British Columbia, Vancouver, Canada
cass at math.ubc.ca