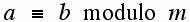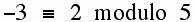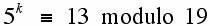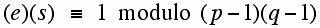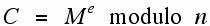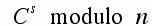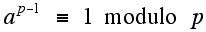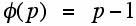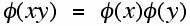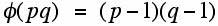Mathematics and Internet Security
Posted April 2006.
When money is transferred electronically, when an email is sent, when a purchase is made online, the users of such systems want to know that the transactions went as planned and were not "hijacked"...
Joe Malkevitch
York College (CUNY)
malkevitch at york.cuny.edu 
Introduction
When a transit strike paralyzed the New York metropolitan area in December, 2005, just a few days before the end-of-the-year holidays, many New Yorkers chose to shop over the Internet rather than brave the hours of delays, long walks, and lack of available cabs to carry out in-the-store shopping. However, some people are still "spooked" by making purchases online, fearing for the security of their transactions.
- Are Internet financial transactions safe?
- Can email that is sent via the Internet be monitored by third parties, causing concern about what one puts into emails?
- Can anything be done about worms, viruses, and other "malware" that seem, unfortunately, to be as much a part of modern life as catching a cold or the flu?
Mathematics is doing its best to try to address these questions with the goal of making on-line transactions totally secure and making the email environment an unalloyed pleasurable addiction. The mathematical tools which are making all this possible are ones that in previous times some thought inapplicable! New techniques are being found for manufacturing faster and smaller chips, which affects the cat and mouse game between those who try to create a secure Internet environment and those who want to steal money without standing on a long line in a bank.

(An illustration of a new lithography technique being developed by NIST for the manufacture of better and faster chips.
Photo courtesy of the National Institute of Standards and Technology.)
The Internet draws heavily on a wide variety of mathematical tools ranging from data compression and error compression techniques, methods for routing messages, and security issues. In honor of Mathematics Awareness Month, whose theme for 2006 is Mathematics and Internet Security, a few of the many issues involved will be highlighted here.
Cryptography
A military commander wants some assurance that the information sent to field commanders does not fall into the hands of opponents. Hence, written communications which can be easily read if intercepted by an an enemy are dangerous. (Asking the messenger to memorize secret messages is not practical, and if one can believe the spy and counter-terrorism thrillers currently on TV, not secure.) Julius Caesar is often credited with one of the earlier attempts at using a cryptological system with a mathematical flavor to disguise messages. It is claimed that he used a system in which each letter of the alphabet in a "plaintext," the original message, is replaced by the next letter of the alphabet, with the last alphabet letter cycling around to be represented by the first letter of the alphabet. Thus, the phrase Caesar Cipher would be replaced by Dbftbs Djqifs. Coming across a message such as this, one is faced with the tremendous range of possible systems that might have been used to disguise the original message. It might confuse the "enemy" for a while. Within the range of what today have come to be called Caesar Ciphers, one could shift the replacement alphabet by r places, rather than 1 place (r =1) in the example above. When r = 5 the phrase Caesar Cipher becomes hfjxfw hnumjw.
However, if a decoder hits on the idea that the way the plaintext is being disguised is to shift each letter by the same number of positions, it is not very much work, with the English alphabet of 26 letters, to try them all. This simple example already shows the interesting connection between "complexity" issues and security, whether it be Internet use of cryptography or military use. In some situations slowing down one's opponent is good enough. If it takes an hour to decode a message whose information content is valueless after an hour, then the coding system has done its job. However, if a message is decoded, then the next time a similar message is intercepted, the time to recover the hidden information could go down from an hour to 3 minutes. Then I must keep finding ways to stay a step ahead of my "enemy." In this discussion I will use the words code and cipher and decode and decipher interchangeably. However, usually a cipher refers to replacing a symbol of a plaintext alphabet by another single symbol from some other alphabet or the same alphabet. By contrast, a code refers to replacing blocks of symbols in the plaintext, by another block of symbols.
There have been many developments in cryptography since the Caesar Cipher. One simple idea is not to use the same word lengths in the enciphered message as in the original. If the word "I" or "a" is left as a single letter in the "ciphertext," then it greatly simplifies the process of breaking the encryption system. Typically, the message is broken up into groups of 5 letters (disregarding spaces between words, and often punctuation) and replaced by 5 other letters. This has the effect of making the coded message look more "anonymous." If the length of the original message is not a multiple of five, then extra symbols, called nulls in the "trade," are added to fill out the needed positions.
Another simple idea is the use of a polyalphabetic cipher, where the alphabet used to encode the plaintext changes with each letter in accordance with some key. Using the key provides a way to change the alphabet used for the encoding as one matches a plaintext letter to a letter in the key. This idea was pioneered by Leone Alberti (1404-1472), who was also a pioneer of projective geometry. It is tempting to believe that such a "complex" system would be unbreakable. However, if the key length is short and there is lots of ciphertext available using the same system, then statistical methods can be used to break the cipher. If a key is used only once and is generated at random, the so-called one-time pad, then the cipher is not breakable. However, key exchange and generation of large amounts of random key present a significant problem for the volume of communications that we want to secure in modern times.

Skipping to more modern times we come to a very important period and figure for the development of mathematics' role in security issues, Alan Turing (1912-1954) .
After Hitler's forces took over countries such as Holland and France, Germany wanted to extend its conquests to include Britain. Britain began an elaborate effort to try to prevent invasion of the British Isles by taking advantage of communications and signals intelligence (patterns in levels of communication traffic that might indicate some special military operation) and information obtained by deciphering coded communication. A special group of individuals was assembled at Bletchley Park, experts in languages and mathematics, to try to glean as much useable information from the enemy as possible. The first successes in breaking German codes was due to the work of Polish mathematicians, including work of Marian Rejewski, who were able to hand over what they had achieved to the British.

(Photo courtesy of NSA, the caption reads "Marian Rejewski, the Polish mathematician
who made the initial breakthrough against the Enigma machine.")
Using the materials from Poland, Turing and his team undoubtedly changed the course of the war (and history) with his efforts in deciphering materials being generated by the German Enigma machine, seen below, as well as other German cryptographical systems.
(Photo courtesy of NSA)
Turing worked with the mathematician Gordon Welchman to develop a specialized "computer" to help break the Enigma-generated codes.
(Bombe courtesy of NSA)
In the United States too, many men and women, including many linguists and mathematicians, were involved with the war effort. Among the most famous of these individuals were William Friedman (who used mathematical techniques though not trained as a mathematician) and his wife Elizabeth (a linguist). The United States' team broke many Japanese codes and thereby were able to change the course of the war.
(Elizabeth Friedman and William Friedman: Photos courtesy of NSA)
Modern cryptography is no longer primarily the concern of the military and diplomats. Cryptography is increasingly applied to maintain capitalism's infrastructure: telecommunications and the Internet. When money is transferred electronically, when an email is sent, when a purchase is made online, the users of such systems want to know that the transactions went as planned and were not "hijacked." The variety of issues here is staggeringly complex and varied. When one party sends a message to another party, one would like to think: a. the message sent was the message that arrived rather than having some other message substituted b. the message sent can not be used in a way that compromises the security of messages sent in the future c. the way that the message was sent does not allow someone in the future to pretend that a message sent by them came from you. The world of "intrigue" that one associates with spies and spying plays out in with no less complexity in the world of Internet security.
Hashing
Hashing is the process of taking a long string and replacing it by a much shorter string in some systematic way. For example, if one started with a poem, one could replace it by the string which gives the number of letters in the poem. At first glance it might appear that hashing involves issues of data compression rather than data security. However, it should also be clear that a hashed string might have cryptological importance because it might be possible to build into the hashing system that it be hard to figure out what the original string was. The complication with hashing is that ideally one wants to avoid having different strings hash to the same string. When this happens one says that a collision has occurred. In the system described above, two poems of exactly the same number of letters would create a collision. Thus, one has to build into one's system what to do about collisions, should they occur. Another desirable feature of hashing designed for security purposes is that when two similar strings are hashed, the results are extremely different. Thus, if someone tries to modify a "secure document" in some small way, that the "intrusion" could be detected because the hash of the two documents, the original and the forged one, would be very different. There is a circle of ideas that's involved in why hashing is very closely tied with the issue of passwords and digital signatures. A digital signature is an electronic identification system analogous to the handwritten signatures commonly used for letters and checks. One wants to have a system which minimizes the dangers of forgery. In the mid-1990's one of the popular hashing systems was MD-5 (Message-Digest Algorithm 5), which was designed by Ronald Rivest of MIT. However, in 1996 in a series of developments let by mathematicians and computer scientists, it became clear that MD-5 had problems with its security, so it was commonly replaced by SHA-1.
Hashing has had an intimate connection with Internet security in that it is a commonly used feature of password management systems. Passwords are not only used for email accounts but they are often used to access commercial services that an individual might subscribe to using the Internet (e.g. newspaper accounts or financial accounts). One favor you can do for yourself is to practice some simple rules for improving password security over the ones that many individuals use. Several standards for hashing systems have unfortunately, in light of concerns about maintaining security, proved to be breakable with available computing resource systems. Recently, SHA-1, considered the workhorse of secure hashing systems, was shown to be vulnerable. This work was done by a Chinese mathematician, Xiaoyun Wang, and her co-workers. There is disagreement about the short term implications of Wang's work. Though it does not appear that available computer resources make it possible to break SHA-1, the progress made by Wang and her colleagues raises the issue that some clever variant of the ideas she has pioneered will place existing systems in danger. More secure systems than SHA-1 are currently known but they are not as speedy.
It might seem that there are so many ways that a crypto-system could be implemented that it would be hopeless to discover the system that was being used and be able to recover the plaintext message from the coded message. There are two common ways to break crypto-systems. One is to use statistical techniques. If one has large collections of "ciphertext," one can look for patterns (using frequency distributions for the symbols that appear) to try to break the system. The other method for breaking the system is that people who use crypto-systems often have "tics" or "mannerisms" that give entry points into deciphering the systems. Perhaps some particular user always begins the message with the same greeting. Perhaps a message always begins with a weather report which allows one to try to guess the way common words are encoded. Another factor is that when a system is widely used, there are typically many people involved in its management. In such cases it is difficult to prevent information about the type of system being used from becoming known. Thus, the methods that are used for attacking substitution ciphers are different from the methods that are based on matrix techniques. Given the practical realities involved, it is widely felt that the proper way to view security is to assume that the person trying to break one's security system knows exactly the type of system one is using. Thus, the "enemy" might know that you are using RSA (explained below) or that you are using a Hill Cipher (matrix oriented system).
Public Key Systems
A major revolution in cryptology occurred in the middle 1970's with the discovery (some say rediscovery) of a new paradigm for codes. In traditional cryptography the two parties that wanted to share secret information arranged a system, which typically required a "key exchange," of a single key. Intuitively, think of a key as a way to "lock" a message that is being sent in secret. If the receiver has an identical key to the sender, then the message can be unlocked. Thus, single key systems involve having a common basis (key) for the person who encrypted a message and the person who decrypted it to operate the crypto-system.
All this changed with the development of Public Key Cryptography. Credit for this development is usually given to Ralph Merkle, Whitfield Diffie and Martin Hellman, though the history of this development is complex.



Whitfield Diffie (Courtesy of Dr. Diffie and Sun Microsystems), Prof. Martin Hellman (Courtesy of Dr. Hellman),
and Dr. Ralph Merkle (Courtesy of Dr. Merkle)
Public Key Cryptology is based on having two keys. One key, used to send a secret message to a particular person X, is publicly available, like a phone number in telephone directory. The second key, which is not made public, is held by X to be used in conjunction with the public key. Another aspect of public key cryptography and modern private key systems is having a method of allowing strangers to confidently exchange keys with each other. Such a system was devised by Diffie and Hellman (using ideas from Merkle) and it is designed to work over a nonsecure communication system. This system was patented, though the patent has now expired. Below we will discuss in a bit more detail the best known of the public key systems, known as as RSA. It is named for its developers Ronald Rivest, Adi Shamir, and Leonard Adleman.
(Adi Shamir, Ronald Rivest, and Leonard Adleman. Their initial work work on RSA dates from the period when they were students at MIT.)
Another popular public key system is due to Taher Elgamal (1984). This method uses ideas about group theory and complexity issues for its security.

(Photo courtesy of Dr. Taher Elgamal)
For both RSA and ElGamal (and other systems) it is useful to know about the congruence concept. Two integers a and b are said to be congruent modulo m (a positive integer, which is at least 2) written:
if a and b leave the same remainder when divided by m or alternatively, that b-a is exactly divisible by m with a zero remainder. Here are some examples:
Note that we can always arrange the number on the right hand side of a congruence to be a number between 0 and (m-1) where m is the modulus. Thus, we could replace 23 by 10 in the last congruence. It is not very difficult to find the value for the "?" in the congruence below:
The idea for doing this is to compute the values of 5, 52, 54, 58, etc. modulo 19 and then use the binary representation of exponent (in this case 72) to help compute the answer. However, the problem of finding the value of k for which the congruence below is valid is much less straightforward:
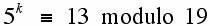
The problem of finding k in a situation such as this is known as the discrete logarithm problem. When the modulus is very large, methods which are appreciably better than brute force are not currently known. The complexity of finding discrete logarithms (for various m, in particular, when m is prime) and many other algorithms that have been used to try to design public key systems, is not fully understood. It turns out that some systems based on NP-complete problems have been "broken" while other systems which depend on problems whose complexity is still not understood fully seem to be holding their own. Next we will give a simplified discussion of the popular RSA system, which is widely used as a security measure on the Internet.
This is a Test
One of the ideas that inspired workers in public key crypto-systems is the notion of a "one-way function." This is a task which is easy to perform but which is hard to "reverse" unless one has additional special information.
If you want to get some feel for the mathematical study of complexity and how this interfaces with security issues, try the following. Use a watch (with a second hand) to see how long it takes you to do each of the following problems:
Problem 1:
Multiply 123457 by 372451. (No calculators or computers please.)
Problem 2:
Determine the factors (I promise there are some, other than 1 and the number itself) of 374251. (No calculators or computers please.)
What you probably discovered was that though it was tedious, you had no difficulty multiplying the two numbers in Problem 1, and if you actually attempted the problem, you probably finished getting the product. However, if you were able to solve Problem 2 it probably took you a lot longer than solving Problem 1. Many people would lose heart before finding the answer.
Is there a sense in which Problem 1 is simple and less complex than Problem 2? In abstract terms, Problem 1 asks for the product of two numbers, in this case, the product of two six digit primes. (A number is prime if its only factors are 1 and itself.) Problem 2 asks for the factorization of a number which is the product of two primes into the factors which were multiplied to get the number. (Given only s, which is known to be the product of two primes p and q, find p and q.)
It is widely thought that there is no really fast algorithm for factoring integers on a "standard" computer but there is no result which shows that factoring is as hard as the problems which are known as NP-complete. The NP-complete problems are ones which are equivalently hard in the sense that if any of them could be solved in polynomial time, then all of them could. On the other hand, if any one of them could be shown to require exponential amounts of time to solve, then all of them would require this amount of work. However, although it is widely believed that these problems do require an exponential amount of work to solve, no one is, in fact, sure. It is thought that there is no "easy" algorithm to factor large numbers, and until recently it was not known whether there was a way to check if a number was prime in polynomial time. Many people were surprised when Manindra Agrawal, Neeraj Kayal, and Nitin Saxena showed there was a polynomial time algorithm to test for primality. Although there are very fast algorithms for checking if a number is prime, the fastest known such algorithms are interesting in that they will certify that a number is prime with very high probability but will on occasion find numbers which are really composite and assert that they are prime. The surprising development of finding a polynomial time algorithm to check for primality means that there is a possibility that factoring can be done using a polynomial time algorithm using some clever but not yet noticed approach. (It is worth mentioning that not all polynomial time algorithms work quickly on the problems that are commonly encountered in practice. Also there are exponential time algorithms such as the simplex method for linear programming that work very quickly in practice, because the problems that the algorithm works poorly on are not those that the simplex algorithm is usually required to solve.)
Here is a very brief description of the well known and widely used RSA approach to public key cryptography. We will assume that the message one wishes to send has been converted from the text (English, say) into pieces or blocks, and each block has been converted to a single number M (for message) which represents that block of the original message. Our job is how to send M securely. Next, one generates two large primes p and q. This can be done relatively easily. (There is debate as to whether picking primes which are "special" in some way leads to a situation where the result is more or less secure.) Now pick a positive integer e (bigger than 1), which is relatively prime to the product (p-1)(q-1). Two integers are called relatively prime if the largest integer which divides both of them is 1. Thus, 12 and 35 are relatively prime though neither of them is prime. Now, one locates a number s such that:
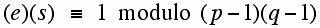
Now, compute the number n = pq, the product of our secret primes.
To send our message number M we calculate C (for cryptogram) by:
The values of e and n constitute the public key. Note that knowledge of n, which is the product of our two large primes, is believed to be of no value to decipher C without being able to factor n.
The recipient of the message must decipher it. This can be done by computing:
The values of s and n constitute the private key of the receiver of the message. These values are used to decrypt back to the original message M.
Why does this calculation give M?
The reason (though the formal details are omitted) involves two classical theorems of number theory, one due to Fermat (1601-1665) and called "Fermat's little" theorem:
where a is an integer relatively prime to p, where p is a prime. The other theorem needed is due to Euler (1707-1783) and is related to the function φ(x) where φ(x) denotes the number of integers relatively prime to x. This function is sometimes call Euler's phi function or the totient function. For any prime p,
Furthermore, if x and y are relatively prime integers, we have the following:
It follows that for distinct primes p and q:
Euler proved a lovely generalization of Fermat's Little Theorem which involves the phi function φ(x):

where x is a positive integer which is relatively prime to the integer a.
In light of the fact that RSA depends for its security on the factoring of large numbers, the company that manages the use of RSA has presented challenges involving factoring to the mathematics and computer science community. Relatively recently a 193-digit number that had been put forward as a challenge was factored. For some history and more recent developments, have a look at this site.
Recently there has been an unexpected concern about the security of RSA and other public key systems that are based on complexity considerations. As traditional computers have become faster and faster it raises the question of whether cryptological systems which use brute force to break the system will be successful. The major commercial traditional code for many years was DES (Data Encryption Standard), developed by the IBM Corporation. Eventually, however, computers became so fast that with the key sizes traditionally used, DES could be broken. As a consequence of the fact that DES was no longer secure a new "standard" had to be developed. This has been done and involves what is known as the Advanced Encryption Standard. This standard uses a system known as Rijndael, which is a combination of the names of Joan Daemen and Vincent Rijmen, the cryptographers who developed the system. During an investigative period prior to being adopted as the new standard to replace DES, Rijndael was subjected to unusually intense scrutiny. When it withstood all attempts to compromise it, it was certified for use. However, Rijndael is considered extremely "elegant" in its mathematical description. Some people consider the very fact that it is so mathematically succinct may lead to its ultimate undoing. Perhaps there is some entry point to breaking this system which has not yet been thought of which grows out of the appealing mathematical structure that it has.
The development of the digital revolution with its reliance on computers and computer supported telecommunications has been based on the use of computers that use a single powerful processor (chip) or a parallel architecture which uses many chips. However, scientists are exploring a new type of computation based on ideas from physics arising from quantum mechanics. This new approach is known as quantum computation. If a quantum computer can be made in practice, the mathematician Peter Shor and others have shown that there are problems for which conventional computers seem to require a long time to solve but which could be solved much more quickly on a quantum computer. In particular, Shor showed that factoring could be carried out more quickly on a quantum computer than on a conventional computer. Thus, in particular, relying for security on RSA when such computers would be available would no longer be a good idea! It remains to see how this active area of physics, mathematics and computer science will play out.
The Internet has changed the way Americans and people around the world interact with each other and lead their lives. If the Internet is to continue to have the positive effect on society that most people perceive it to have had, mathematics will have to continue to be a partner in the Internet's development and evolution.
References
Not surprisingly, the literature devoted to Internet security is rapidly changing. Practices which were secure with slower machines and the best know algorithms at a given time often become insecure on quite short notice. Information about the past and current trends can be found in a variety of places on the web.
Here are some locations to consult:
Computer Security Archive Project.
National Institute of Standards.
The International Association for Cryptologic Research.
Many graduate mathematics departments sponsor research seminars related to cryptography (which often have implications for the Internet). Here is one example, which includes links to papers related to the seminar contents. There are also several research journals that deal with cryptology and Internet security. Websites have emerged (supporting the hypothesis that there is a website for anything and everything) that deal with computer security and cryptology.
Beutelspacher, A., Cryptology, Mathematical Association of America, Washington, 1994.
Bidgoli, H. (ed.), The Internet Encyclopedia, John Wiley, Hoboken, 2004.
Bidgoli, H. (ed.), The Handbook of Information Security, John Wiley, Hoboken, 2006.
Bidgoli, H., (ed), The Handbook of Computer Networks (to appear).
Cheswick, W. and S. Bellovin, A. Rubin, Firewalls and Internet Security: Repelling the Wily Hacker, 2nd edition. Addison-Wesley, 2003.
Churchouse, R., Codes and Ciphers, Cambridge U. Press, Cambridge, 2002.
Clark, R., The Man Who Broke Purple, Weidenfeld & Nicolson, London, 1977.
Coutinho, S., The Mathematics of Ciphers, A.K. Peters, Natick, 1999.
Davies, D. and W. Price, Security for Computer Networks, John Wiley, Chichester, 1984.
Diffie, W. and M. Hellman, New Directions in Cryptography, IEEE Transactions on Information Theory, vol. IT-22, Nov. 1976, p. 644-654.
Diffie, W. and S. Landau, Privacy On the Line, MIT Press, Cambridge, 1998.
Elgamal, T., A public-key cryptosystem and a signature scheme based on discrete logarithms, IEEE Trans. on Info. Theory, vol. IT-31 (1985) 469-472.
Galbraith, S., Elliptic curve public key cryptography, Mathematics Today, 35 (1999) 76-79.
Garfinkel, S. and G. Spafford, Practical Unix and Internet Security. O'Reilly and Associates, Inc., 1996.
Golomb, S., Shift Register Sequences, Holden-Day, San Francisco, 1967.
Hellman, M., An Overview of Public Key Cryptography, IEEE Communications Magazine, May 2002, p. 42-49.
Kahn, D., The Code Breakers, Macmillan, New York, 1967.
Kahn, D., Seizing the Enigma, Souvenir Press, London, 1991.
Koblitz, N., A Course in Number Theory and Cryptography, Springer-Verlag, New York, 1987.
Koblitz, N., Elliptic curve cryptosystems, Math. of Comp., 48 (1987) 203-209.
Koblitz, N and A. Menezes, A survey of public-key cryptosystems, 2004 (available on the web).
Lewand, R., Cryptological Mathematics, Mathematical Association of America, Washington, 2000.
Lidl, R. and G. Pilz, Applied Abstract Algebra, Springer-Verlag, New York, 1984.
Mason, John. Online Privacy Guide: 19 Actionable Steps to Protect Online Privacy, 2017.
Menezes, A. and P. van Ooshot, S. Vanstone, Handbook of Applied Cryptography, CRC, Boca Raton, 1997.
Merkle, R. and M. Hellman, Hiding information and signatures in trapdoor knapsacks, IEEE Trans. Inform. Theory, 24 (1978) 525-530.
Mollin, R., An Introduction to Cryptography, Chapman & Hall/CRC, Boca Raton, 2001.
Rivest, R., and A. Shamir, L. Adleman, A method for obtaining digital signatures and public key cryptosystems, Communications of the ACM, 21 (1978) 120-126.
Schneier, B., Applied Cryptography, Wiley, New York, 1994.
Shor, P., Algorithms for quantum computation: discrete logarithms and factoring, Proc. 35th IEEE Annual Symp. on Foundations of Computer Science, 1994, p. 124-34.
Stallings, W., Cryptography and Network Security, 4th edition, Pearson-Prentice-Hall, Upper Saddle River, 2006.
Welsh, D., Codes and Cryptography, Oxford U. Press, Oxford, 1986.
Joe Malkevitch
York College (CUNY)
malkevitch at york.cuny.edu 
NOTE: Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet can be used to get additional bibliographic information and reviews of some these materials. Some of the items above can be accessed via the ACM Portal, which also provides bibliographic services.