Knots and Their Polynomials-10 Knots and Their Polynomials
What about the left trefoil?


Left- and right-handed trefoilsA diagram for the left trefoil can be obtained by reversingall the crossings in a diagram for the right trefoil:make every overcrossing into an undercrossing.
If we rewrite the skein relation
t-1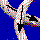 [t] - t
[t] - t  [t] =(t1/2 - t-1/2)
[t] =(t1/2 - t-1/2) [t]
[t]so as to interchange the positionof the undercrossing and the overcrossing, we obtain
- t  [t]+t-1
[t]+t-1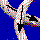 [t]=(t1/2 - t-1/2)
[t]=(t1/2 - t-1/2) [t].
[t].Now let's multiply both sides of the relation by -1:
t  [t] -t-1
[t] -t-1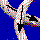 [t]=(t-1/2 - t1/2)
[t]=(t-1/2 - t1/2) [t].
[t].This manipulation shows that the skein relation holds if the undercrossingand the overcrossing are interchanged and at the same time positiveand negative powers of t are interchanged.
If we apply this form of the skein relation to the left trefoil, thecalculation will proceed exactly as it did for the right trefoil,except that the exponents of t will be exactly oppositefrom what they were before. At the end we will obtain
 [t] = - t-4 + t-3 +t-1
[t] = - t-4 + t-3 +t-1which is different from the value for the right trefoil!
On to the next knot page.
Back to the previous knot page.
Back to the first knot page.
Welcome to the
Feature Column!
These web essays are designed for those who have already discovered the joys of mathematics as well as for those who may be uncomfortable with mathematics.
Read more . . .
Feature Column at a glance




