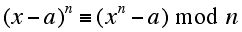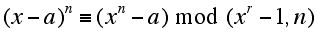Feature Column from the AMS

Primes

6. The right stuff

It takes a special kind of courage to become an astronaut, to undergo the arduous training necessary to try to get the skills necessary for adapting to an environment which is very different from the one we know on a daily basis. Mathematicians who take on unsolved problems of long standing also need to have a special kind of courage. Taking on a long-standing conjecture is a two-edged sword. The knowledge of acclaim and fame for success is accompanied by the risk of investing time and emotional and intellectual energy in a project that may not succeed. Taking such a risk requires a special type of courage, which, fortunately for society and mathematics, pops up regularly.

New mathematics problems come in a wide range of difficulty. Some new questions are simple "exercises" and can be solved by applying well-known theorems in a straightforward way. Solving such exercises begins to develop one's mathematical muscles. Other new questions are hard "exercise." They can be solved using known theorems in a clever way, or with persistence. Other questions reside in an area which requires the putting together of a variety of ideas leading to a solution. The solutions to such questions, which have interest to a reasonably large number of mathematicians, wind up being published in research journals to show other researchers new ideas, methods, and often new problems which grew out of the solution of the old ones.

From time to time, interesting and important problems defy the best efforts of researchers for a sizable amount of time. Among the most famous of such problems was Fermat's Last Theorem, which eventually succumbed to the efforts of Andrew Wiles and Richard Taylor and those that set the stage for their work. This problem had gone unresolved for so long that it took great courage for Wiles to work on it for so long. When a problem is unresolved for a long time, anyone contemplating working on this problem knows that many other smart people have worked on it in the past and not been successful. This can often be intimidating since lots of very able mathematicians have often been attracted to long-standing problems and it does not push one's career along to work for a long time on a problem only not to succeed. (Thus, it is probably good advice to up-and-coming mathematicians not to work on problems that have eluded solution for a long time until they have reached a phase in their careers where they have the "luxury" of failing.)

Another aspect of important discoveries is that the first work is rarely the last word in insight into solving a long-standing problem. Almost invariably ways to shorten and improve the original breakthrough are found. Such was the case for trying to find an algorithm which would show that it is possible to determine in polynomial time whether or not a given integer is prime.

Although many algorithms have been found to test for primality, until very recently, no polynomial time algorithm had been found in 2000 years of on and off effort. Early in August of 2002, three Indian mathematicians demonstrated that they had the right stuff. They announced a proof that there was a polynomial time algorithm for deciding if a number is prime or not. The individuals involved were Manindra Agrawal, Neeraj Kayal, and Nitin Saxena, shown below.

Photograph of Agrawal, Kayal, and Saxena

Not only was their algorithm and the proof that it did what it was supposed to do correct, but given fairly standard number theory background, their work was relatively accessible. Agrawal, Kayal, and Saxena's work has set in motion a chain reaction whereby they and other number theorists have attempted to improve and explore the ramifications of their initial breakthrough.

Let me give the barest hint of how Agrawal, Kayal, and Saxena were able to carry out their breakthrough. Not surprisingly they turned to Fermat's Little Theorem as a starting point. As I have mentioned, this theorem allows one to show for sure that a number is composite but one cannot use it to show that a number is prime. However, from Fermat's Little Theorem one can derive an interesting congruence which holds if and only if the modulus for the congruence is prime (when n and a are relatively prime):

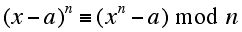
The problem with this congruence is that it involves polynomials rather than numbers, and when n is a large integer these polynomials require lots of computation time to work with. The next idea was that perhaps one could get to work with polynomials of lower degree by dividing the congruence above by another polynomial and considering:

They showed that the above congruence held when n was prime and r and n are relatively prime to a. Their new algorithm grew from a successful investigation of what conditions on a and r allow one to conclude that when the congruence above holds, n must be prime.

The new algorithm which shows that determining if an integer is prime is in the complexity class P and is inspirational in showing that clever creativity is always possible. Hopefully we can look forward to many more such mathematical tours de force in the future!