sphericon 4 The Differential Geometry of the Sphericon
4. Curvature on the Sphericon: the zip-locus
The Sphericon has more complicated curvature singularities than cone points. Along the curves where the cones are zipped together (the zip-locus) there is a 1-dimensional concentration of curvature. The Sphericon World geographers can analyze this curvature by another application of Gauss' Theorem.
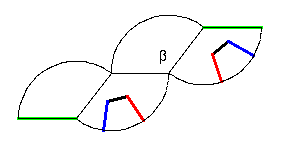
Here they have drawn a quadrilateral that is bisected by thezip-locus. (They can do this without actually crossing thatlocus themselves!). Its red and blue edges aredrawn using straight line segmentsfrom the cone-points to the zip-circles, so they meet thosecircles at right angles.In that way, when the zipping is done, each pair of edgesfits together without forming a corner as seen in the surface.Since they are both straight line segments before the zipping, they willform a single geodesic edge. The resultingfigure has four geodesic edges: one red, one blue and two black.
What are its angles?
- Suppose the pie-slices have radius R,and that the length of the arc intercepted by the quadrilateral isL. If the sides are extended to the cone-points, they will meetat an angle
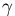 = L/R, in radian measure.
= L/R, in radian measure. - If the quadrilateral is drawnsymmetrically, its angles will all be equal, and equal to(
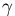 +
+ 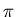 )/2. The sum of the interior angles is therefore2(
)/2. The sum of the interior angles is therefore2(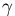 +
+ 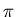 ).
).
By Gauss' Theorem, the total enclosed curvature is equal to this sum minus 2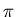 (here n=4), so the total enclosed curvature is 2
(here n=4), so the total enclosed curvature is 2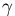 = 2L/R.
= 2L/R.
This calculation does not depend on the height of thequadrilateral away from the zip-locus. The only way to explainthe result is to say that the surface curvature is concentratedalong the zip-locus in such a way that any curve intersecting thezip-locus in an arc of length L will enclose total curvature 2L/R.
On to Sphericon page 5.
Back to Sphericon page 3.



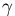 = L/R, in radian measure.
= L/R, in radian measure.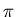 )/2. The sum of the interior angles is therefore2(
)/2. The sum of the interior angles is therefore2(