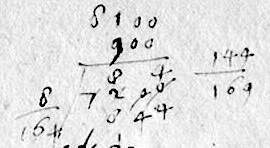Galileo's Arithmetic
The manuscripts allow us very unusual, if not unique, access to the private calculations of a great scientist; it is as if we could look over his shoulder and watch him at work...
 Tony Phillips
Tony Phillips
Stony Brook University
Email Tony Phillips
Introduction
We are very fortunate that many of the handwritten working documents of Galileo Galilei (1564-1642) have been preserved and have been made available for online study. The website Galileo Galilei's Notes on Motion, a joint project of the Biblioteca Nazionale Centrale, the Istituto e Museo di Storia della Scienza, both in Florence, and the Max Planck Institute for the History of Science, Berlin, contains color photographic reproductions of 168 pages of Galileo's work, with transcriptions and high-resolution versions of each image.
 |
A page of calculations (folio 70 recto = f.70r) from Ms. Gal. 72, the collection of Galileo's manuscripts in the Biblioteca Nazionale Centrale, Florence. Larger image. Along with the record of measurements, this page contains examples of all the arithmetic operations, including extractions of square roots. Some items from this page will be analyzed in detail below.
This image, as well as the other six images from Ms. Gal. 72, is reproduced with permission of the Ministero per i Beni e le Attvità Culturali / Biblioteca Nazionale Centrale, Firenze. Further reproduction or duplication in any medium is forbidden.
|
The manuscripts allow us very unusual, if not unique, access to the private calculations of a great scientist; it is as if we could look over his shoulder and watch him at work. From a mathematical point of view they allow us to see the very state of the art in computation in the period 1604-1636 when they were written. In fact they show that in Galileo's hands the use of base-ten place-value notation in arithmetic had reached its modern form. The way he performs multiplication of large numbers, long division and square-root extraction is exactly the way 20th century students were taught. One exception is that Galileo never used a decimal point, and represented numbers smaller than unity by fractions. Another more minor one is that Galileo performed as many steps as possible in his head, and only wrote down the essential.
Before looking at examples of Galileo's calculations, it may be useful to examine how arithmetic was taught in his day. Again we are fortunate to have available online, thanks to the ECHO project, a mathematics textbook published in 1559, just before Galileo was born.
Arithmetic in 1559: Pietro Cataneo's Le Pratiche delle due prime matematiche
Cataneo (born in Siena, died c.1569) is best known as an influential theorist of architecture. But his first published work, Le Pratiche delle due prime matematiche, ("Methods of the first two kinds of mathematics," i.e., arithmetic and geometry) is considered a prototype of the modern mathematics textbook. Cataneo starts by defining the elementary operations for integers and fractions; he begins with addition and subtraction, which are standard.
|
Multiplication. First comes "multiplication from memory" (mutiplicar a la memoria). Cataneo lists the multiplication facts one needs to know by heart: a multiplication table up to $10\times 10$ and the first ten numbers times the numbers $12,\dots, 20, 24, 32, 48$; he then covers multiplication of a several-digit number by a single digit and multiplication by powers of 10. Cataneo presents two methods for multiplying several-digit numbers. The first, per crocetta (crosswise), is the way multiplication was explained by Fibonacci. It is lovely but since there is no trace of it in Galileo's work, it is postponed here to an Appendix. The other, multiplication per biricuocolo, is the method we teach children today. Cataneo's digit-by-digit explanation in the text is illustrated in the margin as shown here.
In Venice this method was called per scachiero (chess-board style), since the numbers are aligned as if on a grid. Biricuocolo was a Tuscan cake, presumably with a grid-like decoration.
|
$$\begin{array}{cccccc} &&&9&7&8\\ &&&3&6&5\\\hline &&4&8&9&0\\ &5&8&6&8&\\ 2&9&3&4&&\\\hline 3&5&6&9&7&0 \end{array}$$ |
|
$$\begin{array}{ccccc} 5&4&2&.&.\\ 7&6&8&9&3\\ 5&4&2&&\\\hline 2&2&6&9&\\ 2&1&6&8&\\\hline &1&0&1&3\\ &&5&4&2\\\hline &&4&7&1 \end{array}$$ |
$)\!\underline{~1~~4~~1~~}{\scriptstyle\frac{471}{542}}$
|
|
Division. For division also, Cataneo presents several different methods. For per testa ("in the head") division, by single digits for example, it is enough to know the multiplication table. Per scapezzo works with multiples of $10$. Per ripiego, literally "by folding" is convenient when the divisor can be broken into small factors, so several consecutive per testa divisions can achieve the result.
As Cataneo reminds us, there are infinitely many divisors, the prime numbers, for which these methods won't work. For such a divisor he presents two possible methods, a danda and a galera. The first is essentially modern fourth-grade long division except for the placement of the elements: Cataneo writes the divisor above the dividend, and the quotient to the right. Here is his example of $76893\div 542$ as worked out in the margin (the text contains step-by-step instructions).
|
"Galley-style" division (per galera) most likely descends from sand-table calculations where one digit would be rubbed out and replaced by another. Here during the computation a digit is crossed out and the substitute is written directly above it. The name is inherited from an earlier format in which the divisor was written below the left-most place of the dividend and then crossed out and rewritten one place to the right with each iteration, digits always positioned vertically so as to leave no grid square empty. The tapering top and bottom of that array had some resemblance to the prow and stern of a ship, hence "galley-style." Caetano just keeps one end, say the prow. He illustrates the method with $87654\div 53$.
|
$$\begin{array}{ccccc} &&0&&\\ &0&\not{2}&4&\\ 0&\not{2}&\not{3}&\not{5}&\\ \not{3}&\not{4}&\not{8}&0&5\\ \not{8}&\not{7}&\not{6}&\not{5}&\not{4}\\ &&&&\\ &&&5&3\\ &1&6&5&3\frac{45}{53} \end{array}$$ |
"See how many times the $5$ of the divisor goes into the $8$ of the number to be divided; it goes $1$ which you write under the $7$ ... , & that $1$ you multiply by the $5$ of the divisor, which makes $5$ again, which you subtract from the $8$ ... leaving $3$ which you write over the $8$ & strike out the $8$; & multiply that $1$ by $3$ the first digit of the divisor, which makes 3 again, which you subtract from the $7$ ... , & $4$ will remain; & mark the $4$ over the $7$ & strike out the $7$ & you will have the remainder 34, which combined with $6$, the next digit ... , makes $346$; now you should see how many times the $5$ of the divisor goes into the $34$ of the $346$; it goes in $6$, which you mark under the other $6$ ... ; & multiply it by $5$ ... & that will be $30$, which you subtract from $34$ & there remains $4$; mark $0$ over the $3$ & cross out the $3$; then multiply that $6$ by the $3$ of the divisor & that will be $18$ which subtracted from $46$ leaves $28$; mark $28$ above the $46$ & strike out the $46$; then you will combine $28$ with $5$, the next digit ..., which makes $285$; so you need to see how many times the $5$ of the divisor goes into the $28$ of $285$, which will be $5$, which you will mark under the other $5$ ... , & multiply it by the $5$ of the divisor & that will be $25$ which subtracted from $28$ leaves $3$; over the $2$ which is over the $4$ you will mark $0$, & strike out the $2$; & multiply the said $5$ by the $3$ of the divisor, which makes 15, & subtracted from $35$ leaves $20$ which you mark above the $35$ & strike out the $35$; & combine the said $20$ with $4$, the first digit ... & that makes $204$; now you need to see how many times the $5$ of the divisor goes into the $20$ of $204$; it would go $4$ times but since the $3$ of the divisor can't go $4$ times into the $4$, first digit of $204$ you will say that the $5$ into the said $20$ goes $3$, which you mark under the $4$ ... ; & multiply it by $5$ from the divisor & that will make $15$, which subtracted from $20$ leaves $5$; mark $0$ over the $2$ & strike out the $2$; then multiply that $3$ by the $3$, first digit of the divisor; & that makes $9$, which subtracted from $54$ leaves $45$ which you mark above the $54$; & strike out the said $54$; under the $45$, the last remainder, you will mark the divisor $53$ & you will have $1653\frac{45}{53}$ as result."
Square roots. Cataneo describes a square-root algorithm organized like the division a danda but distinguishing every other digit of the radicand by a (real or imaginary) dot, starting with the units' place. Here is how he explains the extraction of the square root of $54756$. (This better version comes from the 1546 edition).
|
$$\begin{array}{ccccc} 5&4&7&5&6\\ 4&\mbox{first}&\!\!\!\!\mbox{doub}&\!\!\!\!\!\!\!\!\!\!\mbox{led}&\!\!\!\!4\\\hline 1&4&\mbox{seco}&\!\!\!\!\!\!\!\!\!\mbox{nd}&\!\!\!\!46\\ 1&2&&\\\hline &2&7&&\\ &&9&&\\\hline &1&8&5&\\ &1&8&4&\\\hline &&&1&6\\ &&&1&6\\\hline &&&&0\\ \end{array}$$ |
$(\!\underline{~2~~3~~4~}~$
|
The last dot will be below the $5$, the first digit on the left, and for that $5$ you need to find the closest [integer] root which is $2$, which you multiply by itself to give $4$, which you will write under the $5$, as if dividing
a danda; from that $5$ you subtract the $4$, and that will leave $1$ to which you "give" on the right the $4$, the next digit of $54756$, which will make $14$;
now you need to find a number which, multiplied by the double of the root you have found, i.e. $4$, that product can be subtracted from $14$ and from the remainder, accompanied by the $7$ of $54756$, can be subtracted the product of that number by itself with remainder not larger than the double of the root you will have found, which will be $23$. And thus you will say that this number must be $3$, which multiplied by the double of $2$, i.e. by $4$ gives $12$, which subtracted from $14$ leaves $2$, and accompanied by that $2$ the $7$ of $54756$ will make $27$, from which you will subtract the product of $3$ with itself which makes $9$, and the remainder will be $18$; with this you will accompany the $5$, the next digit and second from right of $54756$ which will make $185$.
Now you need to find a number which multiplied by the double of the root you have found, i.e. the double of $23$ which is $46$, that product can be subtracted from $185$ and from the remainder joined with the $6$, the next digit of $54756$, can be subtracted the product of that number [with itself] with remainder not larger than the double of the root you will have found; so you will say that this number must be $4$, which multiplied by the double of $23$, which is $46$, makes $184$; subtracting this from $185$ will give $1$ with which you join the $6$ of $54756$ which will make $16$, from which you subtract the product of $4$ with itself, and there will be no remainder. So $54746$ can be said to be a perfect square, with root $234$ ...
The passages in italics are tough sledding. We will return to them in analyzing Galileo's approach to this calculation.
Approximation: Cataneo remarks that when the radicand is not a perfect square (and therefore the algorithm gives a remainder), the remainder divided by twice the calculated root should be added to that root. He gives the example of $17=4^2+1$; the algorithm gives integer root $4$ and remainder $1$, so $4\frac{1}{8}$ should be taken as the approximate root of $17$. (Here Fibonacci had gone much farther, explaining that the approximating step could be repeated --an adumbration of Newton's method: here $(4\frac{1}{8})^2 = 17 + \frac{1}{64}$; for a better approximation Fibonacci would add to $4\frac{1}{8}$ the remainder (negative in this case) divided by twice the root, i.e. $\frac{-1}{528}$.)
Comments?
Arithmetic operations in Galileo's manuscripts
Multiplication and division. In this item from f.70r, the multiplication is $1251\frac{1}{2}\times 240$. Galileo adapts the
per biricuocolo format to include fractions. The product is shown as the sum of $1251\times 40=50040$ with the shifted $1251\times 2=2502$ and $240\times\frac{1}{2}=120$; the last term is written $1$ on the third line and $20$ on the second following Galileo's practice of filling empty "squares" in the "grid." The three terms are added to give the final product $300360$.
That product is to be divided by $225\frac{2}{7}$. Galileo handles the fraction by calculating the quotient of $300360\times 7=2102520$ by $225\frac{2}{7}\times 7=1577$. The division is carried out in a hybrid of the
a danda and
a galera formats. The three arguments are placed "american style:" divisor to the left of dividend and quotient written above, digits of the quotient matching corresponding digits of the dividend.

Reproduction forbidden in any medium. See copyright notice above. |
In the guts of the calculation, products and subtractions are all performed mentally; digits that have played their part are struck out; and instead of dropping down the digits "given" by the dividend to the successive remainders, Galileo tacks them on by reading diagonally up; always filling all the squares in an imaginary grid. The result is a replica of the prow of the "galley," but upside-down (allowing Galileo to link a division, as here, to previous operations). If the digits suppressed by Galileo are made explicit (here written $\scriptstyle{\rm small}$), the resut is the configuration used today.
$1577|$
|
$$\begin{array}{ccccccc} &&&1&3&3&3\\ 2&1&0&2&5&2&0\\ \scriptstyle{1}&\scriptstyle{5}&\scriptstyle{7}&\scriptstyle{7}&&&\\\hline &5&2&5&\scriptstyle{5}&&\\ &\scriptstyle{4}&\scriptstyle{7}&\scriptstyle{3}&\scriptstyle{1}&&\\\hline &&5&2&4&\scriptstyle{2}&\\ &&\scriptstyle{4}&\scriptstyle{7}&\scriptstyle{3}&\scriptstyle{1}&\\ &&&5&1&1&\scriptstyle{0}\\ &&&\scriptstyle{4}&\scriptstyle{7}&\scriptstyle{3}&\scriptstyle{1}\\\hline &&&&3&7&9\\ \end{array}$$ |
$\frac{\displaystyle 379}{\displaystyle 1577}$
|
|
Multiplication and square root extraction. This next excerpt from f.70r shows the multiplication $1111\frac{1}{30}\times 500$ and the extraction of the square root of that product. The multiplication is done as above, with $500 \times\frac{1}{30}$ reduced to $50\times\frac{1}{3}$ and approximated as $17$, giving $555517$ as the product.
The square root algorithm shows a fundamental improvement of the a danda-like method explained by Cataneo (and by Fibonacci and Pacioli before him). The earlier authors understood that the odd and even-placed digits of the radicand had to be treated differently, and that each pair of radicand digits contributes a single digit to the root. Nevertheless in the operation the radicand digits were brought ("given") down one by one. This resulted in a convoluted explanation like those shown above in italics in Cataneo's root extraction. To analyze the difference anachronistically, let us look at the spot in Cataneo's operation where he has just brought down the $5$. At that moment the current root is 23, and the next digit of the radicand is $6$. Cataneo has Now you need to find a number which multiplied by the double of the root you have found, i.e. the double of $23$ which is $46$, that product can be subtracted from $185$ and from the remainder joined with the $6$, the next digit of $54756$, can be subtracted the product of that number [with itself] with remainder not larger than the double of the root you will have found. Suppose we call "that number" $x$. Cataneo's sentence translates to the three inequalities $$0\leq 185-46x$$ $$0 \leq ((185-46x)\cdot 10 + 6)-x^2$$ $$((185-46x)\cdot 10 + 6)-x^2 \leq 2\cdot(230 + x)$$ which must all be satisfied by $x$. But if the $5$ and the $6$ are brought down together the problem simplifies to $$0\leq 1856-(460+x)x$$ $$x~ \mbox{is the largest such number.}$$
I don't know if Galileo was taught this improvement or figured it out himself. It appears, slightly mangled, in the work of Georg von Peuerbach (1423-1461). In Galileo's operation the digits are brought down two by two to form a new partial radicand, and the next digit of the root will be the largest single digit which, when appended to double the current root, and then used to multiply that adjunction, is smaller than that partial radicand. This is the way square root extraction was still taught in elementary school halfway through the 20th century. Galileo continues the condensed notation from long division (multiplications and subtractions preformed mentally, and only essential digits recorded) resulting in a galera-like picture. If the operation is written as below with the digits suppressed by Galileo reinserted $\scriptstyle{\rm small}$, it could have been the work of a 20th-century schoolchild. The schoolchild might have continued the calculation by inserting a decimal point and bringing down pairs of zeros to get $745.33012...$; Galileo uses the "remainder over twice the root" fractional approximation: $\frac{492}{1490}$ which in decimals would be $.330201...$.
$$\begin{array}{cccc} &&&7\\\hline &&&\\ &1&4&4~\scriptstyle{\times 4}\\\hline &&&\\ 1&4&8&5~\scriptstyle{\times 5} &&&\\ \end{array}$$ |
$$\begin{array}{|cccccc} &7&&4&&5\\ 5&5&5&5&1&7\\ \scriptstyle{4}&\scriptstyle{9}&&&&\\\hline &6&\scriptstyle{5}&\scriptstyle{5}&&\\ &\scriptstyle{5}&\scriptstyle{7}&\scriptstyle{6}&&\\\hline &&7&9&\scriptstyle{1}&\scriptstyle{7}\\ &&\scriptstyle{7}&\scriptstyle{4}&\scriptstyle{2}&\scriptstyle{5}\\\hline &&&4&9&2 \end{array}$$ |
$\frac{\displaystyle 492}{\displaystyle 1490}$
|
|

Reproduction forbidden in any medium. See copyright notice above. |

Reproduction forbidden in any medium. See copyright notice above. |
Galileo does not always use the fractional approximation; of over 300 square root extractions in this archive, fewer than 80 are completed in this way. Many of the numbers going into the computations come from measurements in his laboratory (there is a list of such data at the top of f.70r); it is unlikely that there were ever more than 3 or 4 significant digits at stake, so the extra precision would not have made sense. This item from f.156r has an example of the calculation of the geometric mean of two numbers, one among many in the collection. Here Galileo calculates $\sqrt{184776\times153072}$. The product gives a nice example of our biricuocolo algorithm; the root is calculated as $168178$. Note that Galileo did not write the last $8$ in the left-hand column of numbers, but only at the end of the root. Note also the prow of the "galley" taking shape in the center of the calculation. |
On five of the folios (117r, 114v, 161r, 132r, 132v), all dated by Stillman Drake to 1608-1609, Galileo uses twice the root plus one in the denominator of the fractional part (there are 8 such extractions).
|
This image shows an item from f.132r, where $\sqrt{7200}$ is calculated as $84\frac{144}{169}$. In fact this is the better approximation when (as in this case) the integer part plus one is closer to the root than the integer part. But on the same page Galileo calculates $\sqrt{1625}$ as $40\frac{25}{81}$ when $40\frac{25}{80}$ is better. Writing $N$ for the radicand, $a$ for the remainder and $r$ for the integer part of the root, it had been known since the Middle Ages that $$ (r+\frac{a}{2r+1})^2 \leq N \leq (r+\frac{a}{2r})^2, $$ so it is possible that on these folios Galileo needed an underestimate of the roots he was calculating. |
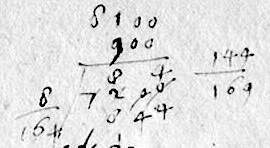
Reproduction forbidden in any medium. See copyright notice above. |
Comments?
Galileo the human spreadsheet
Galileo published Discorsi e dimostrazioni matematiche intorno à due nuove scienze, usually called "Two New Sciences" in English, in 1638. In his discussion of trajectories, he prints a table of ranges ("amplitudes") and maximum heights ("altitudes") of projectiles all fired with the same initial speed, at angles from the horizontal varying from $1^{\circ}$ to $90^{\circ}$. The distances are normalized so that a projectile fired at $45^{\circ}$ will travel 20,000 units, and are described in terms of the semi-parabola representing half the trajectory. Proposition XII explains how to compute the amplitudes, and Proposition XIII how to compute the altitudes from the amplitudes. His calculations for the second proposition are part of the Biblioteca Nazionale archive; all forty-four (see below) are written in columns on three folios, f.103v, f.104r and f.104v. We can (almost) match his work with the sample calculation he gives in "Two New Sciences," here in Stillman Drake's translation.

Reproduction forbidden in any medium. See copyright notice above. |
EXAMPLE
To be found is the altitude of the semiparabola described at elevation $55^{\circ}$. The amplitude, from the preceding tabulation, is $9396$; half of this is $4698$, of which the square is $22071204$. Subtract this from the square of half $~$BO, which is $25000000$ and is always the same; the remainder is $2928796$, of which the square root is approximately $1710$. This, added to half$~$ BO (that is, $5000$), gives $6710$, which is the altitude BF.
Galileo does not have a calculation for $55^{\circ}$ in his notes: he only treats angles from $1^{\circ}$ through $44^{\circ}$. He derives the others using the principle: if two semi-parabolas have angles symmetrically spaced about $45^{\circ}$, their altitudes will be symmetric about the altitude corresponding to $45^{\circ}$ exactly, which is $5000$. The calculation for $35^{\circ}$ matches his description for $55^{\circ}$ except that the root is subtracted from $5000$ instead of being added. (There is an additional curious discrepancy: on the folio the root is calculated --correctly-- as $1711$, whereas in the text it is given as "approximately $1710$").
|
Comments?
Appendix: Multiplication per crocetta
Multiplication
per crocetta (literally, "by the little cross," crosswise) is the algorithm we use today to multiply polynomials:
-
$(a_1x+a_0)\times(b_1x+b_0)=a_1b_1x^2+(a_1b_0+a_0b_1)x+a_0b_0$
-
$(a_2x^2 + a_1x + a_0)$ $\times$ $(b_2x^2 + b_1x + b_0)$ $=$ $a_2b_2x^4 + (a_2b_1 + a_1b_2)x^3$ $+ (a_0b_2 + a_1b_1 + a_2b_0)x^2$ $+(a_0b_1 + a_1b_0)x + a_0b_0$
-
etc.,
but with carrying.
|
$$\begin{array}{ccc} 5&&9\\ (& \Large\mbox{X} &)\\ 4&&7\\ 27&7&3 \end{array}$$ |
In this first example Cataneo applies the crocetta method to $59\times 47$. "Multiply $7$ by $9$, which makes $63$, of which you will mark $3$ in the first place & you save $6$; then multiply crosswise saying $4$ times $9$ makes $36$ & $5$ times $7$ makes $35$, which two products added together & to that sum added the saved $6$ makes $77$, of which you will write $7$ and save $7$; then multiply $4$ by $5$ & add to them the saved $7$, & that makes $27$, which you write down as shown; & you will have $2773$ for the said multiplication." |
|
$$\begin{array}{ccccc} 4&&5&&6\\ &&& \Large\mbox{X} &)\\ 3&&7&&5\\\hline &&&0&0 \end{array}$$ |
"To multiply $456$ by $375$ you write one quantity under the other as shown in the margin and you multiply $5$ by $6$ which makes $30$, of which you put the $0$ in the first place & save $3$; then you multiply $5$ by $5$ & $6$ by $7$ & form the sum of those products & add the $3$ you saved, & that will make $70$, of which you will mark $0$ in the second place & save $7$;" |
|
$$\begin{array}{ccccc} 4&&5&&6\\ && \Large{\times}\!\!\!\!\!\!\!\!- &&\\ 3&&7&&5\\\hline &&0&0&0 \end{array}$$ |
"then you multiply $4$ by $5$, $5$ by $7$ & $3$ by $6$ & sum those $3$ products & add to them the $7$ you saved, & that will make $80$, of which you will mark down $0$ & save $8$. " |
|
$$\begin{array}{ccccc} 4&&5&&6\\ (&\Large\mbox{X}&& &\\ 3&&7&&5\\\hline 17&1&0&0&0 \end{array}$$ |
"then you multiply $4$ by $7$ & $3$ by $5$ & sum those two products together & add to them the $8$ you saved which will make $51$ of which you will mark down one & save $5$; then you multiply $3$ by $4$ & add to them the $5$ you saved & that will be $17$ which when marked down as shown you will have for the said multiplication $171000$." |
Per crocetta is the way multiplication was explained by Fibonacci (
Liber abaci, 1202), who presumably learned it in North Africa. Cataneo mentions that despite "Leonardo Pisano" having demonstrated it for the product of two eight-digit numbers, it is not reliable, except for experts, with numbers longer than three or four digits (presumably because of the heavy load of mental arithmetic).
The translations in this column, unless otherwise noted, are mine.
References
-
Fibonacci (Leonardo of Pisa), Liber abaci (1202) has been translated and printed. L. E. Sigler, Fibonacci's Liber Abaci, Springer-Verlag, New York 2002
-
Georg von Peuerbach's works are hard to find, but there is a reference to his work on square roots in Martin Levey and Martin Petruck, Principles of Hindu Reckoning, University of Wisconsin Press, Madison, 1965
-
The "Treviso Arithmetic" (1478) has been translated as part of Frank J. Swetz Capitalism and Arithmetic, Open Court, La Salle, Illinois 1987
-
Luca Pacioli, Summa de Arithmetica ... is available online in the Fondo Antiguo of the University of Seville.
-
Pietro Cataneo, Le pratiche delle due prime matematiche ... is available online through the ECHO project.
-
All the folios of Ms. Gal. 72 are available online, with transcriptions, courtesy of the Biblioteca Nazionale Centrale, Florence, the Istituto e Museo di Storia della Scienza, Florence, and the Max Planck Institute for the History of Science, Berlin.
-
Stillman Drake, Galileo's Notes on Motion, Istituto e Museo di Storia della Scienza, Firenze 1979 puts the notes into chronological order; current folio numbers are mostly uncorrelated with dates; also Galileo used empty space on earlier folios for later work.
-
Galileo Galilei, Two New Sciences is available in Stillman Drake's translation, University of Wisconsin Press, Madison, 1974
Comments?
 Tony Phillips
Tony Phillips
Stony Brook University
Email Tony Phillips



 Tony Phillips
Tony Phillips