Mathematics and Psychology
We will see that mathematics in its own terms and psychology in its own terms have benefited from their interaction with each other...
 Joseph Malkevitch
Joseph Malkevitch
York College (CUNY)
Email Joseph Malkevitch
Introduction
What subjects are sciences? A list usually begins with physics and a subject that is sometimes taken as part of physics, astronomy. Perhaps studying the stars and noticing the changing patterns of the sky at night were among the first stirrings of mankind's curiosity about his world. Is anthropology a science? What about sociology and economics? And if not, why not?
To answer such questions we need to look at what the word connotes. Most people view chemistry as science while many people would not ordinarily list cooking as a science; they perhaps would say that there are ways in which cooking has some features of science. Lots of cooks run experiments. Perhaps the most contrasting set of human endeavors other than science are the arts. But there is a "science" part of the arts, as shown by the fact that some great artists drew on science to practice their arts and artisanship: Pacioli, daVinci, Brunelleschi, and Dürer.
At the root of the difference between art and science and what are sometimes called the behavioral sciences is measurement. Famous movies that glorify and romanticize cooking talk about the great cooks not necessarily using a recipe but having a feel for how much of one spice rather than another will make the difference between a dish and a great dish. But if one is to be able to repeat the success of a wonderful dish, then one needs to have a recipe, and recipes incorporate measurement and the "algorithm," or procedure by which the steps in creating a cooking masterpiece are carried out.
Tobias Dantzig, (1884-1956) father of the mathematician George Dantzig (1914-2005), wrote the book Number: The Language of Science. Surely he would have been sympathetic to the broader claim that mathematics was the language of science. And Eugene Wigner talked of the "unreasonable effectiveness" of mathematics in physics. Galileo weighs in with "The universe cannot be read until we have learned the language and become familiar with the characters in which it is written. It is written in mathematical language, and the letters are triangles, circles and other geometrical figures, without which means it is humanly impossible to comprehend a single word. Without these, one is wandering about in a dark labyrinth."
People see physics as a science and view as science chemistry, biology, and geology as well. While people talk about the behavioral sciences, as science are they on the same footing as physics, say? Furthermore, is mathematics the language of the social sciences and is mathematics unreasonably effective in the social sciences?
The social sciences, namely anthropology, economics, political science, psychology and sociology don't scream out for having been infused with or guided in their goals by mathematics. However, we will see that mathematics in its own terms and psychology in its own terms have benefited from their interaction with each other.
History
One of the characteristics of sciences is that controlled experiments are performed in order to obtain insights. One of the first to perform experiments in order to get insight into behavioral issues was Ernst Weber.
Ernst Weber (1795-1878) (Courtesy of Wikipedia)
Weber's experiments were in part concerned with perception of sensations. He pioneered the idea of "first noticeable difference." Most people would not call tap water sweet. However, if single grains of sugar are added to the water one at a time, initially, most people will not notice the presence of the sugar, but at some point after continuing to add a single grain of sugar a "threshold" will be reached so that a person will report that water with some amount of sugar tastes "sweet."
It was Weber's student Gustav Fechner who carried on Weber's work in understanding the perception of stimulating different senses, such as hearing, taste, or vision.
Gustav Fechner (1801-1887) (Courtesy of Wikipedia)
The results of what Weber and Fechner did resulted in what today is often referred to as the Weber-Fechner Law. It is often stated in this form:

S refers to the "amount" of a stimulus administered involving some sensation, and S0 refers to the value where the stimulus involving the sensation first becomes "noticeable." C is a constant that depends on the sensation and the person, while p refers to the perceived "amount" of the sensation.
Many thoughts may go through your head in seeing such a "law." Doesn't perception of "loudness" vary from person to person even for the same stimulus? How does one measure the "size" of the stimulus and the threshold level S0? Is the "law" above in the same category as a law such as Newton's Laws or the Newton Law of Cooling which, like the law above, can be formulated in a way that involves the solution of a differential equation? Do mass and loudness have enough in common that when we talk about measuring mass and loudness we are talking about the same "thing?"
Hermann von Helmholtz, best known for his work in physics and physiology, also did work of importance to psychology in the area of showing the connections between sensory information and physiology. Helmholtz was concerned with connections between mathematics and eye movements, nerve conduction, and measurement. For example, he showed that the speed with which a "signal" was sent along a nerve was slower than was thought (some thought such a signal propagated at the speed of light) and could be measured. He "reinvented" the ophthalmoscope in 1851, a device that made it possible to examine the retina of the eye.

Hermann von Helmholtz (1821-1894)
Otto Hölder (1859-1937) was another pioneer of the interface between mathematics and psychology. Best known for an inequality named for him, he provided an important theorem which became a foundation of the way numbers are used for measurements in science. We learn about measurement in lower grades, learn how to use a ruler to measure lengths, and take the first steps towards understanding the nature of the real number system. Most of the attention that is paid to the real number system (infinite decimals) is to their arithmetic operations, addition and multiplication. We study "laws" of arithmetic such as commutativity (e.g. the real numbers obey ab = ba), associativity, and the distributive law, which involves both addition and multiplication. However, in many ways it is the properties of the real numbers as the algebraic structure called a group and the order properties of these numbers that is more important. The fact that we can compare the size of real numbers is critical for measurement.

(Otto Hölder, 1859-1937)
Some of those who have made major contributions to the insights mathematics can bring to psychology have had an educational background that started with psychology and others started with a mathematical background and brought their skills to bear on psychology.
Comments?
Measurement
One aspect of trying to use mathematics in psychology or other social sciences might initially seem below the radar. While the concepts of mass, time, and force are quite subtle and have changed with time, we can come to a reasonable agreement about how to measure these quantities given the insights we have into these concepts at a given period of history.
Imagine we have a group of people and let H(i,j) denote the difference between the heights of person i and person j. We might want to do a study of the changing patterns of height for people who served in the military. When doing statistics in a wide variety of settings or when doing physics, we automatically rely on the fact that though there are questions about what number to use as a height for John, and that while growing up people's heights change, and perhaps, as one grows older one has a smaller height than one had when young, defining a function such as H(i,j) for some mathematical goal is taken for granted. However, what about defining H(i,j) to be the hostility that person i feels for personj or country i feels for country j ? Defining this second function, seemingly parallel to the first example, is much more fraught with issues than the first for many investigators. If one is unsure of the meaning of the numbers that psychologists work with, one must be wary about the conclusions that are derived from these numbers.
What sets physics, chemistry, astronomy, etc. apart is the view that they are quantitative subjects rather than qualitative subjects. We are all used to hearing about a "rule" or "law" where this "law" has a grain of truth to it. However, physics may garner more respect because it quantifies things rather than being qualitative. Lead has more mass than iron and we can say by how much. Pluto is farther from the Sun when it is nearest to the Sun than Mars is when it is farthest from the Sun, and we can actually accurately quantify the distances involved.
Don't we know what is to be known about measurement? Young peoople learn to use a ruler to find lengths, to weigh oneself on a scale, and to read a clock. The results of using devices such as a tape measure, a scale or a clock requires the use of numbers. So it is helpful to be able to work with numbers, particularly to add and subtract numbers so that one can think about how much the items you will carry to school in your pack will total to in volume and in weight. However, it does not take long to realize that some of the issues involved with measurement are not as easy and straightforword as might appear at first glance. Some of the difficulty arises from realizing that the same object can be measured in different ways using different systems of measurement. Thus, we can measure the weight of an orange in ounces (pounds) or grams (kilograms) and we can measure temperature in Fahrenheit or using the Rankine scale. And there are ways to convert between different systems of measurements. 1 kilogram = 2.2 pounds (approximately) and thus one can figure out how to convert 1 pound to kilograms or grams. One also can learn that a particular pumpkin is 3 times as heavy as another, so there are situations where measurements can also involve multiplication or division. As we get older we realize that weight and mass are not the same thing. The same person's weight changes with regard to where he/she is located. By now we are used to seeing pictures of weightless astronauts, and the weight of things on the moon is different from the weight of things on earth. So mass, the amount of "stuff" that a particular object has is a property of the object but the weight of the object depends on its location. However, the concept of mass grows in subtlety again when one studies the physics of special relativity. Thus, the mass of an item which is traveling at a speed close to that of the speed of light will have a different mass from its "rest" mass. Is there a way to put these complications with regard to measurement in perspective by using a mathematical lens? Both mathematicians and mathematical psychologists have contributed to the meaning of measurement and how these ideas gets used in physics and psychology alike.
Utility
When one measures the value of something it becomes apparent that value can be "measured" in different ways. Thus, a $5 bill has a certain value at a given time in terms of what it can buy, but the way one might value money might also depend on factors other than what money can buy. There can be situations where a person might not choose to get additional money even though in a general way most people would rather have more money than less money. For example, if one's back hurt a lot, and one saw a dollar bill on the sidewalk perhaps one might not bend over to pick it up. The same person might have bent over to pick up a $100 bill (and turn it in to the police?) even with an aching back. To help "understand" this sense of valuation in a way that involves something other than monetary value, the idea of utility was developed, where an object would have a certain number of utiles, the utility value of the object.
The intuitive idea behind utility is that people assign "value" to choices or objects according to some system where a number is assigned to the choice or object in such a way that the bigger the number, the more preferred the object. Thus, one can assign utility to money in a way that reflects something more complex than taking into account the additional amount of money. The utility that one has for more money may increase rapidly from having no money to, say, $3,000,000, but as the amount of money one has grows beyond this amount the utility the additional money generates rises more slowly, as in Figure 1.
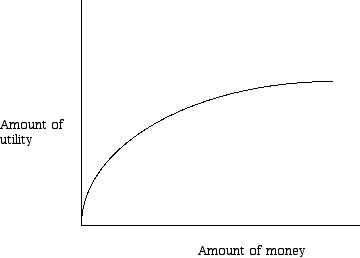
Figure 1. An example of a utility curve for money
Many people in very varied fields have contributed to the development of insight about utilities and how to make decisions or play games based on a utility analysis. Such individuals include the mathematicians Daniel Bernoulli (1700-1782), John Von Neumann (1903-1957), Leonard Savage (1917-1971), R. Duncan Luce (1925-2012) and Peter Fishburn (1936- ), the economists Jeremy Benthem (1748-1832), Oskar Morganstern (1902-1977), and the psychologists Clyde Coombs (1912-1988), Herbert Simon (1916-2001), Amos Tversky (1937-1996), and D. Kahneman (1934- ). Some of these individuals had intellectual interests that cross many fields of study but they did not shy away from the theory or applicability of mathematics.
One goal for a game theorist or psychologist might be to give advice about what to do when faced with the play of a game or a situation where a choice is to be made and from which utility accrues to the player or decision maker. The framework of such advice sometimes takes the form of what a "rational" person, suitably defined, would do in the given circumstances. Given the situation a normative analysis would be to suggest the best thing to do. However, often people don't act rationally when faced with choices. So there is a different approach to analyzing decision behavior which is to study what people actually do when faced with choice behavior. This can sometimes be done by carrying out controlled experiments and what one aims for is a descriptive analysis of the decision situation, the way people act when facing such a decision. Many people have tried to formulate approaches to utility that are normative. For example, if one takes an action which can be thought of as a "combination" of "smaller" decisions, then can one add the utility of the individual parts of the decision to get one number for the whole process. This process often leads to axiomatic studies of the properties of the way the utilities are "tied" to the decision-making process. However, there is also a component of the study of decision making involving "paradoxical" situations where things don't go according to "theory."
A basic idea in probability theory is that of expected value. Suppose I toss a fair coin and when the tossed coin comes up a heads I get $4 and when the coin comes up tails I get $2. The expected value of this "situation" is that of trying to determine what would be the "average" result of having this opportunity many times over. If this experiment is carried out many times the outcome will be a sequence of 2's and 4's, with no particular pattern other than the fact that a fair coin is being tossed. However, since about 1/2 the time a 2 will occur and about 1/2 the time a 4 will occur, the "mean" from a string of these 2's and 4's would be $3. We can think of doing the following calculation: (1/2)(2) + (1/2)(4) = 1 + 2 = 3. More generally, an expected value calculation would weight each of the outcomes possible by the probability (always a real number between 0 and 1) of that outcome and add the terms to get the expected value.
To give another example, involving payoffs that depend on the number of dots that occur when a fair die is tossed, with the payoff being 1 unit for each dot together with one more unit of payoff, the outcomes and their probabilities would be given by the following table:
| Number of dots |
Probability |
Payoff |
| 1 |
1/6 |
2 |
| 2 |
1/6 |
3 |
| 3 |
1/6 |
4 |
| 4 |
1/6 |
5 |
| 5 |
1/6 |
6 |
| 6 |
1/6 |
7 |
If this experiment is carried out many times we get a sequence involving the numbers from 2 to 7. The expected value is given by:
Expected value = 2(1/6) + 3(1/6) + 4(1/6) + 5(1/6) + 6(1/6) + 7(1/6) = 27/6 = 4.5
Note that the expected value need not be an integer nor does it have to be an outcome that is possible for the experiment. Expected value is not a probability, and in particular it can be a negative number. If the payoffs are given by utiles for what may be numerical outcomes rather than the numerical outcomes themselves, we can talk about expected utility for the experiment.
Sometimes the decision that someone is making involves games. One might have to choose between the value obtained in the coin-toss example above versus the value of what one gets from the die-toss experiment. If "rational" behavior means maximizing value or maximizing expected value, we can do experiments to see the way "actual" people rather than "mathematical models" of actual people behave. Do "real" human beings maximize expected utility, and if not, where does this leave the mathematical structures which are used to derive results about utilities and their properties?
Two examples are very telling here. One was developed by the American economist Daniel Ellsberg, who is best known for his association with the Pentagon Papers. The other was developed by the French economist Maurice Allais, who had a background in engineering. Both examples can be set in a variety of ways (e.g. differing numbers) but at their root show that many times people will not apply the "rules" that they are expected to adhere to.
Suppose an urn contains balls of different colors: 30 white balls and 60 other balls that can be either black or green. Though the number of balls that are not white is 60, the breakdown as to how many of these balls are black or green is not known, just that there is some unknown mixture of them.
A ball is drawn "at random" from the urn:
Now you have to make a choice:
Wager 1:
If a white ball is drawn you win $100.
Wager 2:
If a black ball is drawn you win $100.
----------------------------------------------------
Now a ball is again to be drawn from the same urn.
Again you have the choice of two wagers:
Wager 3
If you draw a white ball or a green ball you win $100.
Wager 4
If you draw a black or a green ball you win $100.
----------------------------------------------------
What would you do in each of these situations?
I don't know if you took this into account but you can exactly compute the probability of Wager 1 (30/90 or 1/3) and Wager 4 (60/90 = 2/3) while the exact value of the probabilities in Wagers 2 and 3 can't be determined from the data given.
Experimental data collected when people are given these choices indicate that many people prefer Wager 1 to Wager 2, and Wager 4 to Wager 3.
Is that what you did?
If you apply utility theory to these two situations and want to get the best outcome, what should you do? Which of the Wagers 1 or 2 is best? The prizes are the same so you should prefer Wager 1 to Wager 2 if and only if you think that your chance of drawing a white ball is greater than your drawing a black ball, since this will maximize your expected utility. If you think the probability of getting a black ball and white ball are equal, you will be indifferent between which wager to make.
Which of Wagers 3 and 4 is best? You should prefer Wager 3 to Wager 4 if and only if you think the probability of getting a white or a green ball is larger than the probability of getting a black or green ball.
Now suppose you prefer Wager 1 to Wager 2, meaning you think there is a greater chance of getting a white ball than a black ball. This would seem to suggest that you also think there is a larger chance of getting a white or a green ball than there is of getting a black or a green ball. Hence, if you prefer Wager 1 to Wager 2, it would follow logically that you prefer Wager 3 to Wager 4. Also if you prefer Wager 2 to Wager 1, it would be logical for you to prefer Wager 4 to Wager 3. However, the way people behave is different. Thus, when we model people by saying they will make decisions by maximizing expected utility, we see that our model fails to explain what people actually do. The calculations implicit in intuitive analysis above involve some algebra of manipulating inequalities which can be written down based on the axiomatic conditions which the utilities involved are assumed to satisfy.
Ellsberg's example was not the first of its kind. Maurice Allais's example of choices where many people violate the rules they would have to be using for them to be using expected utility maximization dates to 1953. It is rather more involved than Ellsberg's example and shows that "real people" violate other "axioms" that stand behind the expected utility approach.
It is a hope for those using mathematics in psychology that consistency conditions can be a route to understanding behavior. While it is not surprising (once one sees that the phenomenon can happen) that when a single group takes votes on pairs of alternatives, as a group a majority of members of the group can vote for A over B, a majority can vote for B over C, but a majority of the group may prefer C over A. This situation has come to be called the Condorcet Paradox. In mathematical terms it has to do with the consistency condition called transitivity of a relation. Many relations, equality, parallelism of Euclidean lines, etc. obey transitivity. Transitivity has a nice ring to it. If A is stronger than B and B is stronger than C, then A is stronger than C. While for being "stronger than" may hold in the real world for "stronger" (and as one changes one's sense of what to interpret "stronger" to mean, the assurance one has may disappear), other relations don't obey transitivity, as Condorcet's example shows. The "formal definition" of this idea is formulated this way:
For all members of a set (collection) S where there is a relation R which is defined for pairs in the set S:
aRb and bRc implies that aRc
The example above (Condorcet Paradox) shows the that the relation "beat in a two-way race" need not be a transitive relation.
However, what about transitivity for a single individual when making choices? Can it happen that a person prefers alternative A to alternative B, and alternative B to alternative C, but still prefers alternative C to alternative A?
I have tried the following "experiment" in some courses I have taught. Give people a reasonably large collection of fruit to think about: apple, banana, cherry, fig, grape, lime, and orange. Now ask the person on a separate piece of paper to write down for each pair of these fruits, which of the fruits in the pair is preferred (denoted this relation by P) to the other, no ties allowed. Using the first (lower case) letter of a fruit as its "name" someone might write: f P l, to indicate they prefer eating a fig to a lime. This "test" will produce 21 pieces of paper, the number of pairsings of different fruit in our set of 7 fruit. If people carry out this task one pair at a time and are not able to go back and adjust prior preferences, often they wind up producing a chain of preferences that violates transitivity. When questioned about this they often will "correct" some items. When asked the cause of the "inconsistency" they will often say something in the following spirit. The person prefers sweeter things to less sweet things, but the person also prefers "firmer" fruit to less firm fruit, and when one "factors" in what may be "conflicting" ways of viewing the same objects from different points of view, they realize they were not "consistent" about the whole collection of fruits. Human behavior is complex to analyze, and the motivations humans have for their behaviors are complex. Often the way that information is framed about a decision that has to be made results in different reactions. What is your reaction to having surgery where death occurs 9% of the time compared with surgery where the survival rate is 91%?
Not only have people interested in mathematical psychology studied "utility" and preference behavior from a theoretical and behavioral point of view, they have also looked at game theory and the way that people play games. No mathematician has done more to obtain insight into these matters than R. Duncan Luce (1925-2012). Luce was a student at MIT where he received a doctorate degree in algebra and went on to publish over 100 papers on a wide range of topics related to the interface of mathematics and psychology. One of his most important publications was a joint book with Howard Raiffa called Games and Decisions. This book, though written in 1957, remains a wonderful exposition and survey of game theory and decision theory as well as other topics related to mathematical psychology. While lots of progress has been made since the book was written, it is still a remarkably cogent and valuable entry point to these fields. When I first read this book it was like reading a novel, filled with exciting ideas which dealt with matters that I had never been exposed to or thought about before.

(Robert Duncan Luce, Photograph courtesy of Carolyn Scheer Luce)
Comments?
Psychology and the theory of games
Although the theory of games has antecedents in the famous work of Von Neumann and Oskar Morgenstern, relatively soon after this seminal work the ideas were latched on to by researchers in both political science and psychology. Psychology after all is concerned in part with what behavior people exhibit in various situations. Since there are games which have paradoxical properties, perhaps experiments with games that have paradoxical aspects would provide a window into the way rational people behave when faced with choices that "stress" rationality. So let me begin with an example of a paradoxical game, or more precisely a family of games, often called Prisoner's Dilemma.
| |
Column 1 |
Column 2 |
| Row I |
(80, 80) |
(0, 100) |
| Row II |
(100, 0) |
(4, 4) |
Table 1 (Payoff matrix for Prisoner's Dilemma)
The game above has two players Row and Column who independently make a decision to play the actions they have available to them. For example, Row's actions are to choose (play) Row I or Row II, and Column has the choice of two columns to play. The entries in the table are the payoffs, which are known to both players, who must make their choices without consulting each other. How should Row play? The troubling feature of this game is that it seems whatever Row's opponent does, it makes sense to play Row II, because for either choice by Column, Row's payoff is higher. Because of the symmetry of the game Column reasons equivalently. If both Row and Column both reason in this way they play Row II and Column 2 with the seemingly pleasant result that they always win. However, they would win much more if they always played Row I and Column 1 respectively. The "paradoxical" aspects are strengthened when the payoffs in Table 1 are altered to the values shown in Table 2
| |
Column 1 |
Column 2 |
| Row I |
(80, 80) |
(-60, 100) |
| Row II |
(100, -60) |
(-10, -10) |
Table 2 (Payoff matrix for Prisoner's Dilemma)
As before, "rationality" suggests Row play Row II and Column play Column 2 because doing this does better for each regardless of the choice of their opponent. However, now rational play yields regular losses (if this game is played over and over again) for both players when a sizable gain can accrue for playing Row I by Row and Column 1 by Column.
It is worth noting that if the players "trust" each other, then in Table 2, if they play 34 times each player earns (34)(80) = 2720. However, suppose after 33 plays of the game Column reasons this way: If my opponent Row plays Row I on this last play, and by now he "trusts" that I will play Column 1, I can get a modest improvement in payoff, and "punish" my opponent by playing Column 2. Some players will reason this way.
This suggests that behavior in playing the game in Table 2 may depend on:
a. How much the players "trust" each other
b. How many times the players play the game, which may be once, exactly K times where K is more than 1, or a finite number of times but with no specific value after which play stops.
Thus, the way people behave when faced with games such as the ones in Tables 1 and Table 2 may depend greatly on the many "variables" going beyond the actual numbers in the tables. A psychologist who was a pioneer in using the way people play games as a laboratory to understand behavior was Anatol Rapoport (1911-2007).

Anatol Rapoport (1911-2007), Courtesy of Wikipedia
He (with coauthors) wrote the books The 2x2 Game and Prisoner's Dilemma. These books looked at the classification of two-person games, where each player had two choices of actions when the game was played, and discussed the results of experiments when these games were played under different circumstances. For example, would men play Prisoner's Dilemma differently when playing against other men as compared with when they played against women? How did the relative sizes of the payoffs, and whether some of them were negative, affect the play of the game? There is a large literature, including some funded by the U. S. Defense Department during the "Cold War" that tried to get insight into the way paradoxical games such as Prisoner's Dilemma and the even more "volatile" game known as Chicken (which can be used as a model for various confrontation games that occur in "real life" play out.
Comments?
Kinds of measurement "scales"
There have been many attempts to convey measurement information using "scales" of different kinds. The person who popularized and theorized about this approach was the psychologist Stanley Smith Stevens who tried to organize a "hierarchy' of scales for "measuring" which showed that richer information was obtainable for the "stronger scales" in the hierarchy. The scales Stevens called attention to were: nominal, ordinal, interval, and ratio scales. His work was to some extent a reaction to work by the psychologist N.R. Campbell. Campbell argued that psychology could never carry out "measurement" in the same way that was done in a science like physics. Stevens reacted to this by trying to show that there were different "levels" of measurement. After more mathematical insights into measurement (axiomatic approaches) there continues to be discussion about "over selling" at what level various quantities in psychology can be "measured." The psychologist Joel Michell has written extensively and persuasively that psychologists often make unfounded claims that suggest that some of what they "measure" stands at the same level of science as when physicists measure quantities.
Here in informal language are some of the commonly discussed "levels" of measurements. The underlying idea is to assign either a non-negative real number or a real number to some object that one encounters in the world outside of mathematics in the hope of using these numbers to better understand the phenomenon (objects) one is studying. So one might want to measure spiciness, length, intelligence, time, artistic ability, temperature, strength of a hurricane, or mass.
Nominal scale
Numbers are used as names only and don't connote size information.
Example:
Human chromosomes are named using numbers, hence, chromosomes 6 and 8.
Ordinal scale
Numbers are used to indicate size order but one can't divide the numbers or subtract them with any meaning. One also has to be careful if higher numbers should be interpreted to mean a "stronger" or "weaker" signal.
Example:
Saffir-Simpson Hurricane Wind Scale In the Saffir-Simpson Hurricane Wind Scale a storm at the 1 level is less severe than a storm with higher numbers, In some scales designed, for example to have people rank movies, one uses from 1 to 5 stars, the higher number of stars indicating a "better" movie. So typically regular moviegoers know that 4-star movies have been rated as "better" than 2-star movies. In some situations, however, number "1" is the best.
Interval scale
An interval scale is one in which the numbers used are such that the difference between the numbers at different values in the scale can be properly compared.
Example:
The most familiar example of an interval scale is temperature. Whether one uses degrees Fahrenheit or degrees Centigrade, when working with Fahrenheit degrees, there is the same temperature difference between 5 and 11 degrees as there is between 70 and 76 degrees. However, the 70-degree temperature is not 14 times as large as the 5-degree temperature. When an interval scale is used, the 0 point on the scale is chosen arbitrarily.
Ratio scale
A ratio scale is one in which the numbers used are such that not only are the differences between the numbers at different points of the scale comparable, but one can also compare the results of dividing the numbers. Thus, 80 kilograms is twice 40 kilograms and 30 kilograms is twice 15 kilograms.
Example:
Mass and length are examples of things that can be measured on a ratio scale.
Although it might not seem apparent at first glance, scale type has an important relationship with statistics. Suppose that one writes down the number of the chromosome that a list of genes associated with the development of cancers of different kinds is located on. If one computes the mean of these numbers what has one found out? The answer is nothing. Since the number used for chromosomes is from a nominal scale, it makes no sense to compute the mean of these numbers. One can compute the mode for these numbers and this may provide some "insight." After all, the reason why we use statistics for modeling the world is to get insight. Thus, statisticians worry about what scale type the numbers they are being asked to obtain insight about are drawn from. Students are often asked to evaluate their teachers on a scale that runs from 1 to 5 with 5 being a better rating. Does it make sense for one to compute the arithmetic mean of these ratings to determine "teacher quality?" Not if these numbers are on an ordinal scale! For ordinal scales one can "legally" use the median of the scores but not the arithmetic mean. A teacher who receive 1's from half the class and 5's from the other half is different from a teacher who receives 3's from an entire class.
When mathematicians (see below for some of these individuals) started to investigate scale type, it was realized that what Stevens had done was not complete, and that it helped to clarify whether the numbers in the scale were all real numbers or only non-negative real numbers. Another issue that mathematics called attention to was what functions that mapped the scale values to themselves were allowed. The controversy about scale types has emerged because building on Stevens' scale types, some individuals have argued that when one has modeled some behavioral phenomenon (e.g. "intelligence") using an ordinal scale, it appear that it's really acceptable to act as if the numbers one has are actually on an interval scale. Interval scales allow one to use the arithmetic mean and standard deviation while the ordinal scale does not. For many people this blurring of the use of ordinal and interval scales has caused much confusion and allowed policy decisions regarding educational practices to be made on what looks like scientific evidence when, in fact, the critics argue that what has been done is not scientific.
Comments?
Measurement theory
In a sense the mathematics of measurement theory began with the work of Otto Hölder when he showed mathematically how one could, thinking of the real numbers as an Archimedean ordered group, show how to model real-world quantities like mass using the real numbers. The essential step in doing this rigorously was to show that the addition for real numbers corresponded to something that one could do with masses in the real world that behaved in a way that one could model the process of combining masses in the real world with an "operation" that corresponded to adding the real numbers associated with the masses. This process can be done using the idea of a balance scale. In the discussion here, I am using English words in an informal way, and sometimes in mathematics these words are used in a technical way that gets blurred in an informal discussion. One will often hear a phrase like: we have a "test" that measures, say, artistic ability. This connotes using numbers to measure ability in the same way that numbers measure mass. But no one seems to have successfully showed how to measure a quantity like artistic ability so that what one gets is an interval scale. To do this we would have to be able to say that if Jack, after taking a certain training session, increased his artistic ability from 30 to 40 while Mary increased her artistic ability form 50 to 60, these 10-point growths represent equal accomplishments. However, no one has been able to show how to interpret growth of artistic ability in situations of this kind as numbers that can be added in a way that mirrors addition of real numbers. Using words like "intelligence" or "mathematical ability" or "being career-ready" may make some people believe that what is being done is on the same footing as measuring the distance from the earth to Mars compared with measuring the distance of the earth to the Moon. Physics works in the sense that the time when an eclipse of the Moon will start in Providence, Rhode Island can be calculated with extraordinary accuracy. However, some people may be tempted to use a "measure of college readiness" with the same assurance that they can use "the eclipse will occur at 9:42 p.m." even though this seems unwarranted because many scales developed in education settings are not truly the interval scales that some claim them to be.
Measurement theory as a special subdivision of mathematics is assigned the value 91C05 (a nominal scale) in the classification (taxonomy) of mathematics that is used by the American Mathematical Society. Relatively little attention was given to this area of mathematics after Hölder until the work of Dana Scott, Patrick Suppes (1922-2014), Joseph Zinnes, and R. Duncan Luce in the late 1950s. It is noteworthy that the backgrounds of these individuals was very diverse: logic, philosophy, educational philosophy, and algebra and game theory. This work set out to continue the insights of Hölder and to react to the work of Stevens. The culmination of this line of research was in the three-volume series of books by David Krantz, R. D. Luce, and P. Suppes. David Krantz was an undergraduate mathematics major at Yale but got his doctorate in psychology from the University of Pennsylvania. More recently, important contributions to mathematical psychology have been made by Fred Roberts and Jean-Claude Falmagne.
In this look at the way mathematics and psychology have interacted I have just scratched the surface. I have not even mentioned whole areas on concern such as the way learning occurs. Much work has been done of this topic, notably by William K. Estes. Other important contributors were R.R. Bush and Fredrick Mosteller.
One way to get a good idea of the richness of what is going on in this field is to look at the contents of the articles in two premier journals of the field:
Journal of Mathematical Psychology, and
British Journal of Mathematical and Statistical Psychology.
The fruitful collaboration between mathematics (and statistics) will no doubt grow and continue to get stronger.
Comments?
References
A rich collection of articles by R. Duncan Luce and Louis Narens is available here (Luce) and here (Narens)..
Dowling, C, and F. S. Roberts, P. Theuns, eds. Recent Progress in Mathematical Psychology: Psychophysics, Knowledge Representation, Cognition, and Measurement. Psychology Press, 2014.
Edwards, W. (ed.), Utility Theories: Measurements and Applications. Boston:
Kluwer. (1992).
Ellsberg, D. . Risk, ambiguity and the Savage axioms. Quarterly Journal of
Economics, 75 (1961) 643-669.
Hardcastle, G. L., S. S. Stevens and the origins of operationism. Philosophy of Science 62 (1995) 404–424.
Kahneman, D., Thinking, fast and slow, Macmillan, 2011.
Krantz, D., and Luce, D., Suppes, P., Tversky, A. Foundations of measurement, Vol. I: Additive and polynomial representations, 1971.
Lord, F. M., and M. R. Novick,. Statistical theories of mental test scores., Addison–Wesley, Reading,, 1968.
Luce, R. D., Uniqueness and homogeneity of ordered relational structures. Journal of Mathematical Psychology, 30 (1986) 391–415.
Luce, R. D., Measurement structures with Archimedean ordered translation groups, Order 4 (1987). 165–189.
Luce, R. D., Quantification and symmetry: commentary on Michell 'Quantitative science and the definition of measurement in psychology'. British Journal of Psychology, 88 (1997) 395–398.
Luce, R. D., Utility of uncertain gains and losses: measurement theoretic and experimental approaches, Mahwah, N.J.: Lawrence Erlbaum., 2000.
Luce, R. D., Conditions equivalent to unit representations of ordered relational structures. Journal of Mathematical Psychology, 45 (2001) 81–98.
Luce, R. D., and D. H. Krantz, P. Suppes, and A. Tversky. Foundations of measurement, Vol. 3: Representation, axiomatization, and invariance. Academic Press, 1990.
Luce, R. D., and L. Narens. "Classification of concatenation measurement structures according to scale type." Journal of Mathematical Psychology 29, (1985): 1-72.
Luce, R. D. and J. W.Tukey, Simultaneous conjoint measurement: a new scale type of fundamental measurement. Journal of Mathematical Psychology, 1 (1974) 1–27.
Michell, J., Measurement scales and statistics: a clash of paradigms. Psychological Bulletin, 3 (1986) 398–407.
Michell, J., Quantitative science and the definition of measurement in psychology. British Journal of Psychology, 88 (1997) 355–383.
Michell, J., Measurement in Psychology – A critical history of a methodological concept. Cambridge: Cambridge University Press, 1999.
Michell, J., Is psychometrics pathological science? Measurement – Interdisciplinary Research and Perspectives, 6(2008). 7–24.
Narens, L. (1981a). A general theory of ratio scalability with remarks about the measurement-theoretic concept of meaningfulness. Theory and Decision, 13, 1–70.
Narens, L. (1981b). On the scales of measurement. Journal of Mathematical Psychology, 24, 249–275.
Narens, L., Abstract Measurement Theory, The MIT Press, Cambridge, 1985.
Narens, L., Theories of Meaningfulness, Lawrence Erlbaum Associates, 2002.
Narens, L., Introduction to the Theories of Measurement and Meaningfulness and the Use of Invariance in Science, Lawrence Erlbaum Associates, 2007.
Narens, Louis, and R. Duncan Luce. "Measurement: The theory of numerical assignments." Psychological Bulletin 99, no. 2 (1986): 166.
Roberts, F. Measurement theory, Cambridge U. Press, Cambridge, 1985.
Roberts, F., Measurement Theory, with Applications to Decisionmaking, Utility, and the Social Sciences, Encyclopedia of Mathematics and its Applications 7, Addison-Wesley, 1979, Reprinted by Cambridge University Press, 2009.
Rozeboom, W.. Scaling theory and the nature of measurement. Synthese 16 (1966) 170–233.
Stevens, S. S., On the Theory of Scales of Measurement, Science 103 (2684): (1946) 677–680.
Stevens, S. S., Mathematics, measurement and psychophysics. In S. S.
Stevens (Ed.), Handbook of experimental psychology (pp. 1–49). New York: Wiley, 1951.
Stevens, S. S., Psychophysics. New York: Wiley, 1975.
Suppes, P, and D. Krantz, R. Luce, and A. Tversky, Foundations of measurement, Vol. 2: Geometrical, threshold, and probabilistic representations. Academic Press, New York, 1989.
Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet can be used to get additional bibliographic information and reviews of some these materials. Some of the items above can be found via the ACM Portal, which also provides bibliographic services.
 Joseph Malkevitch
Joseph Malkevitch
York College (CUNY)
Email Joseph Malkevitch


 Joseph Malkevitch
Joseph Malkevitch






