Upgrading Slums Using Topology
In this column, we'll look at a recent paper by Christa Brelsford, Taylor Martin, Joe Hand, and Luis Bettencourt describing recent work that uses topology and graph theory to first identify slum neighborhoods and to then propose strategies for upgrading street networks in slum neighborhoods cost effectively. ...
Introduction
About one billion people currently live in slums, and, as our world is increasingly urbanized, this number is expected to grow. UN-Habitat, a United Nations program whose mission is to promote socially and environmentally sustainable human settlements, estimates that, without sustained and coordinated action, this number could grow to three billion by 2050.
In its Millennium Declaration, the United Nations announced goals "to have achieved by 2020 a significant improvement in the lives of at least 100 million slum dwellers" and "by 2030, [to] ensure access for all to adequate, safe and affordable housing and basic services."
UN-Habitat defines a slum household as one characterized by "lack of access to an improved water source, lack of access to improved sanitation facilities, lack of sufficient living area, lack of housing durability and lack of security of tenure." Indeed, many residences in a slum have no address and cannot be easily reached by a vehicle, which makes it difficult to provide emergency medical and fire services. The delivery of essential services, such as sanitation and clean water, is also complicated by this lack of access.
To meet these stated goals, UN-Habitat calls for the physical upgrading of slums to improve access for residents. Indeed, UH-Habitat writes, "Economically, upgraded slums trigger local economic development, improve urban mobility and connectivity and integrate an enormous economically productive sphere into the physical and socioeconomic fabric of the wider city." This task means providing neighborhoods with clean water, effective waste management, and routes for the delivery of emergency services. More specifically, studies show that physically upgrading street networks to improve access to basic services leads to better living conditions and greater economic opportunity for residents.
Of course, cities such as Boston, with its seemingly haphazard, organic street layout, and Salt Lake City, organized on an underlying Cartesian coordinate grid, illustrate the fact that cities exist in a various of geometric configurations. For the most part, efforts to describe optimal geometric designs of cities and neighborhoods have been unsuccessful.
Notice, however, that the definition of a slum household focuses on a lack of access, which we may interpret mathematically as a lack of connectivity. This means that topology, rather than geometry, may provide a more appropriate perspective on this problem.
In this column, we'll look at a recent paper by Christa Brelsford, Taylor Martin, Joe Hand, and Luis Bettencourt describing recent work that uses topology and graph theory to first identify slum neighborhoods and to then propose strategies for upgrading street networks in slum neighborhoods cost effectively.
Before describing their work, we note two important features of this problem. First, local stakeholders must have a voice in any process both to ensure that specific local needs are addressed and to empower local residents. Second, this is a large-scale problem affecting large numbers of people; our ability to propose solutions using a common set of principles would be improved if some aspects of its study could be automated. In particular, is there a way to automate the identification of slum neighborhoods and the creation of a set of recommendations for upgrades?
Identifying slum neighborhoods
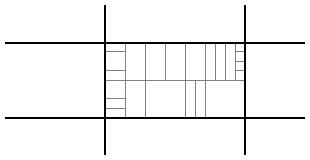
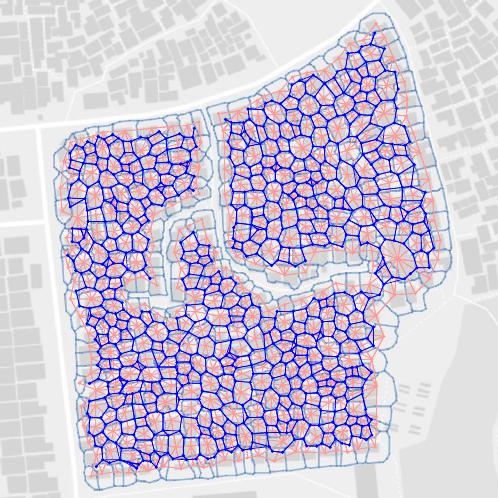
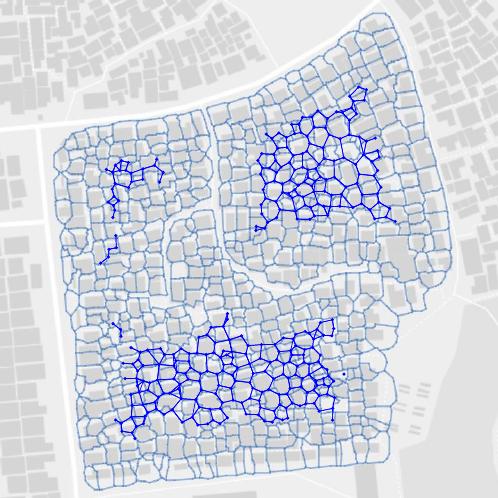
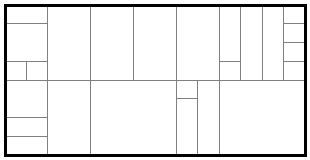
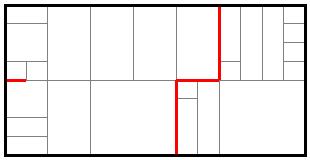
First, we would like to develop an algorithm to identify neighborhoods in which residents lack access to the city street network. Consider, for the instance, the neighborhood shown below. Here we see a system of streets, represented by the dark parallel lines. Inside one city block, we see the individual parcels, indicated in gray, which could represent businesses or residences.
Let's focus on that city block. Notice that each parcel is adjacent to a portion of a street so that each parcel has access to the street network.
By contrast, here is another city block with some interior parcels that do not have access to the street network.
We would like to algorithmically detect these interior parcels and measure their lack of access to the street network. To do this, we will represent the city block as a two-dimensional planar complex of vertices, edges, and faces.
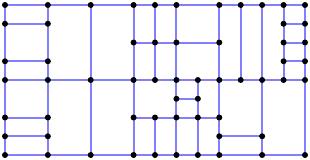
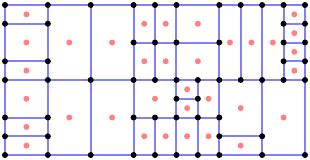
We denote this complex by $S_0$. By a face in this complex, we mean a two-dimensional region bounded by edges; notice that each face of $S_0$ represents a parcel of the city block. From $S_0$, we form an associated planar complex $S_0'$ known as its weak dual. Each face of $S_0$ forms a vertex of $S_0'$ (in pink).
An edge connects two vertices in $S_0'$ if the corresponding faces in $S_0$ share an edge. Each interior vertex of $S_0$ gives rise to a face in $S_0'$.
Because $S_0'$ is again a planar complex, we may repeat this process forming $S_1 = (S_0')'$, the weak dual of the weak dual. Notice that faces in $S_1$ correspond to vertices in $S_0'$, which correspond to faces in $S_0$. Seen in this way, we may think of $S_1$ as obtained from the original complex $S_0$ by removing the faces adjacent to the street network. Faces in $S_1$ correspond to parcels that require crossing at least one internal boundary to reach the street network.
This means that faces in $S_1$ correspond to interior parcels that lack access to the street network. Of course, we can repeat this process to form $S_2 = S_1''$.
The faces in $S_2$ correspond to parcels in the city block that require us to cross at least two internal boundaries to reach the street network.
From here, we can continue this process defining complexes $S_{k+1} = (S_{k}')'$. Brelsford and collaborators define the block complexity of a city block to be one less than the number of times we repeat this construction before the resulting complex $S_k$ is a tree. That is, if a block has block complexity $K$, then $S_{K+1}$ is a tree.
If we consider the city block in which each parcel is adjacent to the street network, we find that $K=0$ and say that the block is universally accessible.
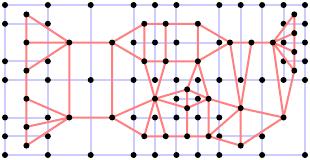
The block in Cape Town, South Africa, shown below, is an example with a block complexity of 6.
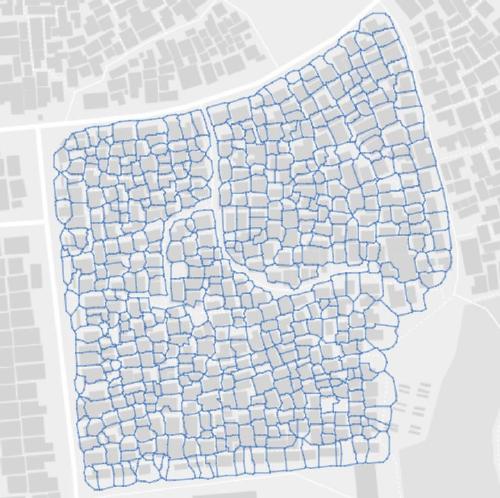 |
| Reprinted by permission of Brelsford et al. |
Here we see $S_1$
and $S_3$.
In practice, maps can be created in a variety of ways. Some are created by local communities or using governmental records; others are created using digital imagery and machine-learning techniques.
The algorithm we have described gives a computationally effective way to determine the block complexity. In addition, the algorithm identifies parcels in the block that are in need of access. We will now turn to the problem of providing access to those parcels.
Reblocking
Now that we have identified the parcels in a block lacking access to the street network, we will consider strategies for making them accessible. To do this, we will upgrade existing paths in the block thereby adding them to the street network. This process, whose goal is to make the block universally accessible, is known as reblocking.
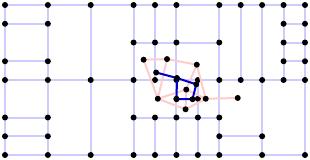
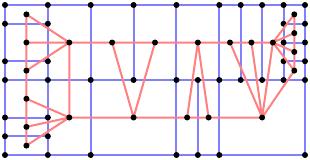
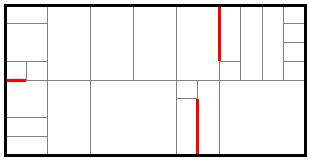
We could naively view this as a simple optimization problem by stating that we would like to add the shortest possible length to the street network to make the block universally accessible. For instance, we could reblock the following block
by adding the red streets below:
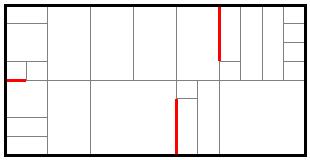
In practice, however, it may not be computationally feasible to find the optimal solution. While it is straightforward to find the shortest path from each interior parcel to some point on the street network, adding internal paths between interior parcels may produce a shorter solution as seen here.
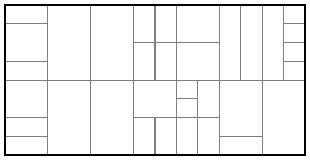
In addition, the paths dividing parcels can vary considerably, which means that some paths are poor candidates for use in a reblocking solution. Shown below is a map of a neighborhood in Mumbai showing the variation in the width of paths dividing parcels.
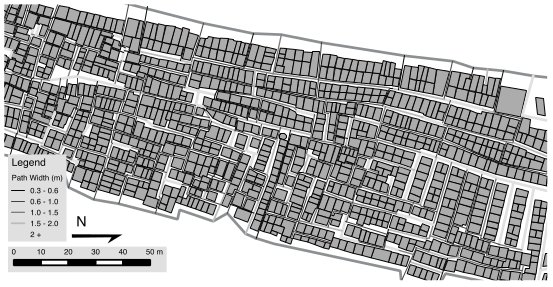 |
| Reprinted by permission of Brelsford et al. |
Furthermore, neighborhoods may have particular priorities, based on local social or economic factors, that would favor a reblocking solution that does not minimize length.
For this reason, Brelsford and collaborators use a statistical process to create a collection of reblocking solutions. In particular, we choose an internal parcel and find the shortest path making that parcel accessible along with a number of other short paths. This gives a set of $m$ paths; we denote the length of the $i$-th path by $l_i$. On this set of paths, we introduce a probability distribution where the probability of each path is proportional to $l_{i}^{-n}$ for some positive power $n$. In practice, $n=8$ is chosen empirically. Simply said, this probability distribution favors the choice of a shorter path.
To generate a reblocking solution, we randomly choose one of the paths making our parcel accessible and add that path to the street network. This addition cannot increase the block complexity of the block.
At this point, we begin over with the new block: we use our dual graph construction to find the block complexity of the new block and identify internal parcels. We choose an internal parcel, identify a set of $m$ short paths making it accessible, and randomly choose such a path. Repeating this process until the block is universally accessible produces a reblocking solution.
The value of this strategy is that it allows us to consider paths that are internal to the original block in a way that is computationally feasible. In addition, running this algorithm a number of times creates a collection of feasible reblocking solutions. These can be presented to local residents and stakeholders to determine the best solution that addresses local concerns and needs that cannot easily be built into an algorithm.
Decreasing travel times
As seen in our simple reblocking solution, minimizing the length of streets we add to the street network adds a number of cul-de-sacs to the network. If a path were added that created a cycle in the street network, one edge in the path could be removed, which results in a shorter path that leaves the block universally accessible.
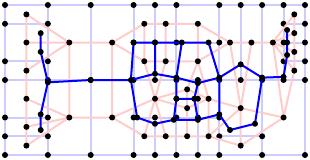
Consider the reblocking solution for a block in Cape Town shown below where the added streets are shown in blue.
 |
| Reprinted by permission of Brelsford et al. |
Notice that there are many examples of parcels that are physically close to one another yet traveling from one to another using the street network requires a long trip. While the block is now universally accessible, travel between parcels is inconvenient due to the travel distance and resulting congestion along the route. Beginning with a solution to the reblocking problem, we would like to make further upgrades to improve access.
Given two parcels, $i$ and $j$, Brelsford and collaborators define the travel distance $T_{i,j}$ to be the minimum distance between the parcels along the street network. They visually represent the travel distances in a colored matrix where blue represents a short travel distance, green an intermediate distance, and yellow and red long distances.
 |
| Reprinted by permission of Brelsford et al. |
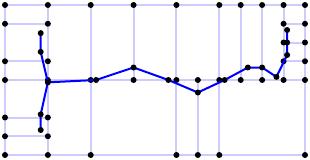
We would like to bring down the average travel distance by adding relatively short streets to the street networks. To determine how to add a street, we consider a parcel $p$ and define $G_p$, its geometric travel distance, to be the average distance between the centroid of $p$ and the centroids of all other parcels. The on-network travel distance $N_p$ is the average distance to the other parcels traveling along the street network.
For each parcel, we compute the ratio $G_p/N_p$ to measure how well connected that parcel is to other parcels in the block. The parcel $p^*$ with the minimal ratio is the least connected. Once we have identified $p^*$, we find the parcel $q$ whose ratio of the geometric travel distance to $p^*$ to the on-network travel distance to $p^*$ is smallest. We then add the shortest path connecting $p^*$ to $q$ to the street network.
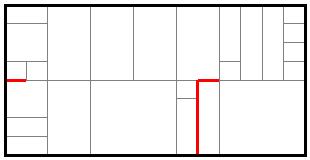
Applying this strategy to our simple reblocking solution
leads us to upgrade a relatively short path while decreasing the average travel distance.
Shown below is the result of performing this operation twice to the neighborhood in Cape Town. Notice how this small addition has a dramatic effect on the travel distances $T_{i,j}$.
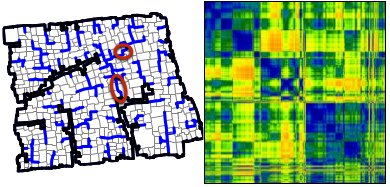 |
| Reprinted by permission of Brelsford et al. |
Summary
The techniques outlined in this column and described more fully in the paper of Brelsford et al are being applied to reblock neighborhoods in Mumbai and Cape Town through a process led by local communities and governments. As the authors state: "We believe that only the current convergence of science, technology, and contextually appropriate people-centric design practices can deliver the necessary fast change in the millions of neighborhoods worldwide that require upgrading."
The authors make available the Python code used in their reblocking work, along with much of their data, at The Open Reblock project.
Aromar Revi, Director of the Indian Institute for Human Settlements has written:
It is the transformation of our urban landscapes that will enable us to end poverty, to provide basic services, housing, sustainable transportation, and to create an environment in which not only can human rights be actually delivered but also prosperity be available to everybody across the world.
Mathematics clearly has an important role to play in this transformation.
References
-
Christa Brelsford, Taylor Martin, Joe Hand, and Luis M.A. Bettencourt. Toward cities without slums: Topology and the spatial evolution of neighborhoods. Science Advances. Vol. 4, No. 8. 29 August 2018.
More technical details are available in the Supplementary Materials.
-
UN-Habitat. Streets as Tools for Urban Transformation in Slums. 2014.
-
UN-Habitat. The Challenge of Slums – Global Report on Human Settlements 2003 2003.
-
UN-Habitat. Slum Almanac 2015-2016. 2015.
-
Michael Batty. The New Science of Cities. MIT Press. 2013.
- Sergio Porta, Paolo Crucitti, and Vito Latora. The network analysis of urban streets: a primal approach. Environment and Planning B. Vol. 33, No. 5, 705–725. 2006.
-
Sergio Porta, Paolo Crucitti, and Vito Latora. The network analysis of urban streets: a dual approach. Physica A. Vol. 369, No 2, 853 - 866. 2006.


 David Austin
David Austin