More Measles
In this column, I shall say more about modeling the progress of an epidemic. ...
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
Email Bill Casselman
Introduction
This is the second Feature Column in which I discuss the mathematics involved in the transmission of measles. The first one made a few very brief remarks about how a mathematical model might track the progress of an epidemic, and then discussed the phenomenon of herd immunity, which enables a population as a whole to become immune to the disease even though not all individuals are immune. In this column, I shall say more about the first topic--i. e. say more about modeling the progress of an epidemic.
As in the earlier column, my intention here is not to come even close to a detailed analysis, but just to explain basic phenomena.
What's to be explained?
In late September 2019 a single case of measles was reported on one of the islands of the South Pacific nation of Samoa. It was followed by several more, the number of cases building slowly at first but then eventually growing rapidly:
What possible theory can account for such phenomena? For example, could one have predicted the eventual size of the epidemic from early data? Could one have predicted its timing?
The answer to the first question is almost certainly "no". This epidemic seems to be somewhat unusual. When one infectious person appears in a population that is largely vulnerable to a disease he will infect a certain number of individuals that he comes in contact with. Each of them will infect roughly the same number, and so on. So at the beginning of an epidemic one expects exponential growth. That is not evident here. (Why not?)
Infected people will eventually recover from a disease like measles, and they cannot subsequently be reinfected. As time goes on, the number of immune people will grow, and infected people will come into contact with fewer and fewer susceptible ones. The epidemic will slow down. If no preventive measures are taken, such as patient isolation or vaccination, nearly all the population will have been eventually infected. In the Samoa epidemic, a mandatory vaccination program was begun in mid-November, and after the new vaccinations took effect (a period of roughly 10 days), the graph begins visibly to flatten.
The parameters of a disease
There is a simple and very basic model for such epidemics. It divides a population into a small number of subsets, and keeps track of the sizes of these subsets from one day to the next, starting with an initial partition. The process depends on a very small number of parameters: (1) the basic reproduction number ${\bf R}_{0}$--the number of people infected by a single case appearing in an unprotected population; (2) the length of time $P$ from when a person is infected to when he in turn becomes infectious (the pre-infectious period); (2) the length of time $D$ that he is infectious.
For measles, ${\bf R}_{0}$ is about $13$, $P$ is about $8$, and $D$ is also about $8$.
It is very important to realize that these data are not exact, but generally vary over a small range according to circumstances. Underlying them is some kind of probability distribution, and they should definitely be interpreted as rough, even poorly known, averages. For example, in this model the degree of contagion remains constant for a period of $D$ days, while in reality a person may well be more contagious at certain times than others.
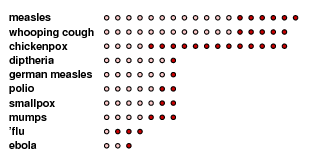
Of these parameters, it is ${\bf R}_{0}$ that is at once most subtle and most significant. The following table displays approximate lower and upper limits for the value of ${\bf R}_{0}$ associated to several diseases. Measles is very contagious.
The basic SEIR model
There is a standard basic model of epidemics of general diseases similar to measles, in which a case of the disease confers immunity (unlike, say, malaria or HIV). It is unrealistically simple, but nonetheless suggestive. Its principal value is probably that if a real epidemic differs from this model one will want to understand why.
In this model the population under consideration is partitioned into five states:
- S: susceptible to infection
- E: exposed (and infected) but not yet infectious
- I: $\kern 1pt$ infectious
- R: recovered
- V: those who have been vaccinated or had the disease previous to the current epidemic
Those in categories $R$ and $V$ are immune. Those who have been vaccinated are effectively in group $R$, through a kind of virtual infection. One can assume $V$ is contained in $R$ if people are not vaccinated in the epidemic, by specifying $R(0)$ to be $V(0)$. In addition, it is valuable to keep track of the time elapsed (say, in days) since a person's last state transition took place. But I'll not do that here.
For some diseases, and in particular measles, there is a possible further category:
- A: asymptotic (not yet showing symptoms) but infectious
For measles, the period in which this happens last for several days, and it makes measles especially dangerous. But although the distinction between $I$ and $A$ is important in practice, since it is only patients with symptoms who are quarantined, I'll ignore this distinction in what is to come.
I'll simplify things quite a bit, and keep track of the state of an epidemic in five numbers--the sizes of each of the relevant categories listed above. But already in this characterization the lack of reality will be apparent, because these numbers will be floating point approximations to integer values. And we'll keep track of states at fixed intervals of time $n \, dt$. In fact, I'll assume that $dt = 1$ day. So we are tracking numbers $$ S(t), \quad E(t), \quad I(t), \quad R(t), \quad V(t) $$ at times $t = 0$, $1$, $2$, ... days after an initial case.
How does the state at time $n+1$ change from that at time $n$?
It turns out that this change of state will be fairly simple, so that tracking a model epidemic will require just specifying an initial state. For example, a single infectious person appearing in a susceptible population of size $N$ will have $$ S(0) = N - 1, \quad E(0) = 0, \quad I(0) = 1, \quad R(0) = 0, \quad V(0) = 0 \, . $$
In all examples I'll look at, I'll take $V(t)$ to be a constant $V_{0}$.
More about parameters
The principal parameter of an epidemic is its basic reproduction number ${\bf R}_{0}$. (This is conventional notation. It is not my fault that there is no relation between the $R$ of ${\bf R}_{0}$ and the $R$ of $R(t)$.) This is defined to be the average number of people directly infected by one person appearing in a large population in which everyone is susceptible. This is necessarily a somewhat theoretical notion, since in the modern world it is hard to find such populations, but it is nonetheless an important concept. The number ${\bf R}_{0}$ doesn't have to be an integer, since it is just an average. It is dimensionless, but it can be expressed in an illuminating fashion as a product of ratios that do have dimensions. Explicitly $$ {\bf R}_{0} = (\hbox{number of infections per contact}) \cdot (\hbox{number of contacts per unit of time}) \cdot (\hbox{amount of infectious time per infection}) \, . $$
It is useful to have this factorization, since it helps you keep track of assumptions going into our model, and with luck might suggest how to measure ${\bf R}_{0}$ when a new disease appears. For example, it should be clear that it depends in social structure, since the rate of contacts varies. In particular, one expects ${\bf R}_{0}$ to be higher than average in an epidemic spreading inside a school, with a lot of contact. In one study the value of ${\bf R}_{0}$ in such a case was estimated to be around $30$.
There is a variant of ${\bf R}_{0}$ that is useful to be aware of. An infectious person is capable of infecting ${\bf R}_{0}$ others in a totally susceptible population, but as an epidemic develops, more and more people become immune to the disease, and the number of susceptibles decreases. In this situation, if an infectious person has ${\bf R}_{0}$ potentially infecting contacts, only a fraction of these can in fact become infected. The fraction is $S(t)/N$. Therefore he infects in one day $({{\bf R}_{0}/ D })\cdot ({ S(t) / N })$, if $N$ is the population size. The effective or net infection number is therefore $$ {\bf R}_{\rm net} = {\bf R}_{0} \cdot { S(t) \over N } \, . $$
Change of state
(S) If there are $I(t)$ infectious individuals then the number of new cases in one day is $$ {{\bf R}_{\rm net} \over D } \cdot I(t) = {{\bf R}_{0} \over D }\cdot { S(t) \over N } \cdot I(t) \, . $$ Hence $$ S(t + 1) = S(t) - {{\bf R}_{0} \over D } \cdot { S(t) \over N } \cdot I(t) = S(t) - {{\bf R}_{\rm net} \over D } \cdot I(t) \, . $$ If $$ \lambda(t) = {{\bf R}_{0} \over D } \cdot { I(t) \over N } $$ then this becomes $$ S(t + 1) = S(t) - \lambda(t) S(t) \, . $$
(E) The number of people who are infected but not contagious at time $t$ is increased by the susceptibles who become infected, and is decreased by those who transition to an infectious state. Let $F$ be the rate of transition. If $P$ is as above the number of pre-infectious days, then $F = 1/P$. We have $$ E(t + 1) = E(t) + \lambda(t) S(t) - F E(t) \, . $$
(I) The number of people who are contagious is increased by those who transition from the previous state, and decreased by those who recover. Let $\Omega$ be the rate of recovery. If $D$ is as above the number of infectious days, then $\Omega = 1/D$ and $$ I(t + 1) = I(t) + F E(t) - \Omega I(t) \, . $$
(R) Finally, on the assumption that the size of the population remains constant: $$ R(t + 1) = R(t) + \Omega I(t) \, . $$
Summary
With $$ \lambda(t) = {{\bf R}_{0} \over D } \cdot { I(t) \over N } $$ We have $$ \eqalign { S_{t + 1} &= S(t) - \lambda(t) S(t) \cr E_{t + 1} &= E(t) + \lambda(t) S(t) - F E(t) \cr I_{t + 1} &= I(t) + F E(t) - \Omega I(t) \cr R_{t+1} &= R(t) + \Omega I(t) \, . \cr } $$ It is curious, and of some purely mathematical interest, that if I define $$ \eqalign { s(t) = { S(t) \over N } \cr e(t) = { E(t) \over N } \cr i(t) = { I(t) \over N } \cr r(t) = { R(t) \over N } \cr } $$ these equations become ones in which $N$ does not occur.
The presence of the factor $I(t)$ in $\lambda(t)$ makes this what a mathematician calls a non-linear system of equations--the various terms do not scale in a linear fashion. In any case, if one starts with known conditions, one can compute approximate values of all these variables for as many days as one wants. In fact, it is very easy to set up a spreadsheet to do this once ${\bf R}_{0}$, $P$, and $D$ are known. To simulate an epidemic, choose some initial values for $S(0)$, $I(0)$, $E(0)$, and $R(0)$ as well as $V_{0}$ and then compute in steps the values of the variables for all variables.
Examples
The first thing one probably wants to do with the technique outlined above is to run a few examples in order to get some feel for what happens.
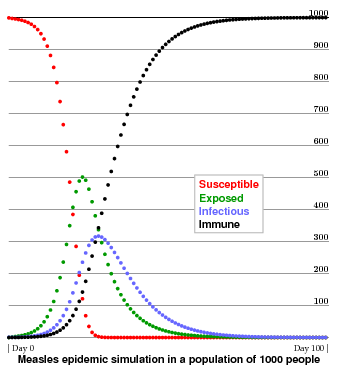
The following figure illustrates the progress over 100 days of a simulated measles epidemic (${\bf R}_{0} = 13$, $P = 8$, $D = 7$) in in a totally susceptible population ($A(t) \equiv 0$) of 1000 people, starting out from the introduction of one case. Qualitatively, it looks very reasonable. Note the lag between infection and infectiousness.
The next figure illustrates what happens when 50% of the the initial population is immune at the start. It looks like in the very long run, everybody will be either initially immune or will have had measles, but that is not the case--instead the number of susceptibles has a non-vanishing limit that will be extremely small if ${\bf R}_{0}$ is large. But for ${\bf R}_{0} = 2$, this part of the population will be about 20%.

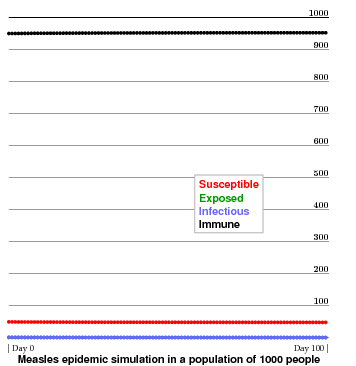
In the next example, I take 95% of the population to be initially immune. In this case, the initial immunity is high enough to lead to herd immunity--that is to say, a definite percentage of the population is still susceptible. The initial infection dies out very quickly. Those who are susceptible at the beginning, for example those who cannot be vaccinated, remain susceptible without damage. This is true of young children, for whom the recommended age for vaccination, for various reasons, is about 15 months. Vaccination thus becomes a civic duty, not just a wise personal choice.
The Samoa measles epidemic of 2019
Early in 2019, as explained in a BBC news item, an epidemic of measles broke out in New Zealand. There is a fair amount of traffic between New Zealand and the small island nation of Samoa (population 196,000), partly because of the large number of Samoans working in New Zealand, and it is likely that sometime late in September 2019 someone who had been infected in New Zealand arrived in Samoa and started an epidemic in Samoa. I have been told that at least the genetic markers of the Samoa variety of measles are the same as those found in New Zealand. The first case in Samoa seems to have been recognized on September 28.
It took a while for the government of Samoa to realize exactly what was happening, or at least to understand what was going to happen. The number of cases increased slowly through September, but was quite sizeable by the middle of October
By October 20, 169 cases had been reported. and one death. The government issued its first press release concerning the epidemic on October 16. Another report came out on November 4, by when there had been 513 cases reported and 3 deaths. On November 13, a national emergency was declared. At this point there had been 1608 cases reported, and the number was growing rapidly. Roughly half of the afflicted were children.
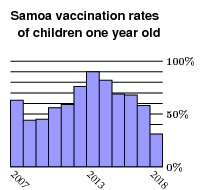
All this should not have been much of a surprise. Measles vaccinations reached more than 90% of children one year old in 2013, but had declined steadily since:
The vaccination rate plummeted a couple of years ago, when an extremely unfortunate maladministration of vaccine had resulted in two deaths. This led to a gross misperception of risk. In any case, it was apparent to many that Samoa in September of 2019 was a kind of time bomb ready to explode. That measles can be infectious without symptoms means that it would not have been practical to keep out all infectious travelers.
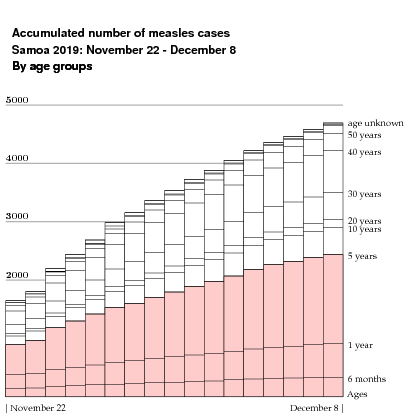
From November 22 through December 8 the Samoan government's Twitter feed reported measles cases by age groups:
In this graph, the high vaccination rates of earlier years is perhaps evident in the low incidence for ages $10$ and higher, although it might not be so clear why the age group $10 - 19$ escaped so well. The unfortunate decline in vaccination rates is equally evident for recent years. Measles is a very dangerous disease for the very young, and there were many fatalities:
The government Twitter feed stopped posting age statistics on December 8, but continued to report the accumulated number of cases. In addition, David Wu supplied me with data prior to November 22. The plot below, repeated from the beginning of the column, summarizes all I know about the record of measles cases. Keep in mind that it is likely that not all cases were reported.
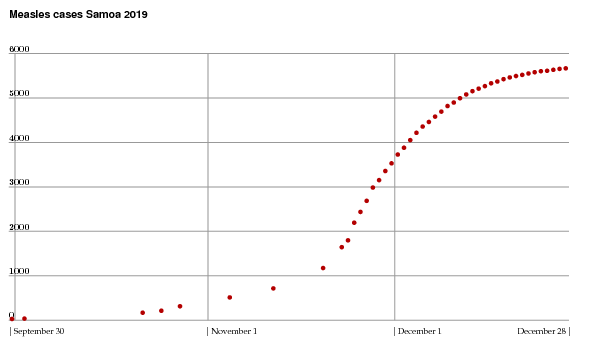
A well-publicized mass vaccination campaign began on November 20, and even though it takes time for a vaccination to take effect, this has clearly affected the development of the epidemic. Also, much international aid arrived. By now (I am writing on December 29) the epidemic is almost over. There have been (as of today) a total of 81 deaths associated to it. This is a shocking number, but not unusually high for fatality statistics. Measles is a dangerous disease! I find it curious that when I was young it wasn't widely known to be so, and certainly not to me. In those days there was no vaccine, and everybody just assumed without much anxiety that a case of measles was an inevitable feature of normal life.
Variations
The Samoa epidemic is distinguished by its size. One consequence is that random events have been smoothed out. In contrast is an epidemic of measles that occurred in an American boarding school in 1934. It was apparently begun by a single case, and then spread rapidly. The progress of the epidemic is shown in the following graph:
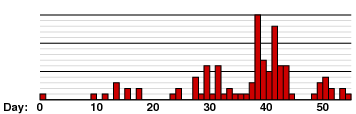
(Redrawn from W. L. Aycock, `Immunity to poliomyelitis',
American Journal of Medical Science 204, 1942)
A very different picture. Approaches to epidemics that take randomness into account are discussed in Chapter 6 of the text by Vynnycky and White.
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
Email Bill Casselman


 Bill Casselman
Bill Casselman