
Mathematical ImageryMathematical artists create strong, stunning works in all media and explore the visualization of mathematics
Shapes and Tilings :: Edmund Harriss
I am a mathematician and artist, fascinated by patterns, both theoretical and visual and their communication. My research is based on substitution tilings, tilings with a scaling symmetry like the Penrose Tiling. I write about ideas on maths, art and communication on my blog, Maxwell's Demon.
— Edmund Harriss (University of Leicester)

Printed on Canvas 24" x 24". The Ammann-Beenker tiling is the eight-fold sibling of the more famous, five-fold Penrose rhomb tiling. It was discovered independently by R. Ammann and F. Beenker. Like the Penrose tiling, the Ammann-Beenker can be constructed by two particular methods. The first method is uses the substitution rule, and the second method is to construct the tiling as a planar slice of a four dimensional lattice (in much the same way that a computer draws a line using the pixels of its screen) and then project this to the plane. See more information. This was a commission for the School of Mathematical Sciences at Queen Mary. It is one of a pair with Ammann Squares, exploring aspects of the Ammann-Beenker Tiling. It appeared "Bridges London, 2006," by Mike Field (Notices of the AMS, June 2007).

Printed on Canvas 36" x 36". This is based on the Ammann-Beenker Tiling. Along with Ammann Squares this work explores the extension of the work of Raymond Brownell (www.raymondbrownell.com) to more complicated geometry. The Ammann-Beenker tiling is the eight-fold sibling of the more famous, five-fold Penrose rhomb tiling. It was discovered independently by R. Ammann and F. Beenker. Like the Penrose tiling, the Ammann-Beenker can be constructed by two particular methods. The first method is uses the substitution rule, and the second method is to construct the tiling as a planar slice of a four dimensional lattice (in much the same way that a computer draws a line using the pixels of its screen) and then project this to the plane. See more information.
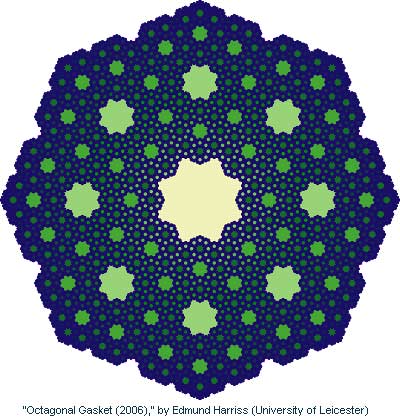
Printed on Canvas 36" x 36". This image is based on a version of the Sierpinski Gasket with octagons rather than triangles.

A pattern built of just four images (two up to rotation). You can make some some patterns yourself.

Sculpture System No. 5 (2009)" by Richard Grimes (www.richardgrimes.net) and Edmund Harriss (University of Leicester). Deltahedra are polyhedra where all the faces are regular triangles. Sculpture system 5 is a system to build any deltahedron using triangular shapes that hinge together. A huge variety of polyhedra can be made using just twenty of these shapes. The actual sculpture was built by a group of volunteers who also designed the final shape that was actually built.

Sculpture System No. 5 (2009)," closer view, by Richard Grimes (www.richardgrimes.net) and Edmund Harriss (University of Leicester). Deltahedra are polyhedra where all the faces are regular triangles. Sculpture system 5 is a system to build any deltahedron using triangular shapes that hinge together. A huge variety of polyhedra can be made using just twenty of these shapes. The actual sculpture was built by a group of volunteers who also designed the final shape that was actually built.


