On cluster algebras from unpunctured surfaces with one marked point
Abstract
We extend the construction of canonical bases for cluster algebras from unpunctured surfaces to the case where the number of marked points on the boundary is one. We show that the cluster algebra is equal to the upper cluster algebra in this case.
1. Introduction
Cluster algebras were introduced in Reference FZ1, and further developed in Reference FZ2Reference BFZReference FZ4, motivated by combinatorial aspects of canonical bases in Lie theory Reference L1Reference L2. A cluster algebra is a subalgebra of a field of rational functions in several variables, and it is given by constructing a distinguished set of generators, the cluster variables. These cluster variables are constructed recursively and their computation is rather complicated in general. By construction, the cluster variables are rational functions, but Fomin and Zelevinsky showed in Reference FZ1 that they are Laurent polynomials with integer coefficients. Moreover, these coefficients are known to be non-negative Reference LS.
An important class of cluster algebras is given by cluster algebras of surface type Reference GSVReference FG1Reference FG2Reference FSTReference FT. From a classification point of view, this class is very important, since it has been shown in Reference FeShTu that almost all (skew-symmetric) mutation finite cluster algebras are of surface type. For generalizations to the skew-symmetrizable case see Reference FeShTu2Reference FeShTu3. The closely related surface skein algebras were studied in Reference MReference T.
If is a cluster algebra of surface type, then there exists a surface with (possibly empty) boundary and marked points such that the cluster variables of are in bijection with certain isotopy classes of curves, called arcs, in the surface. Marked points in the interior of the surface are called punctures, and the surface is unpunctured if all marked points lie on the boundary. Moreover, the relations between the cluster variables are given by the crossing patterns of the arcs in the surface. In Reference MSW, building on earlier work Reference S2Reference STReference S3Reference MS, the authors gave a combinatorial formula for the cluster variables in cluster algebras of surface type. In the sequel Reference MSW2, the formula was the key ingredient for the construction of two bases for the cluster algebra, in the case where the surface has no punctures and has at least two marked points.
1.1. Bases
Our main result, Theorem 2, shows that the basis construction of Reference MSW2 also applies to surfaces without punctures and with exactly one marked point. The proof of this result consists in showing that the Laurent polynomials associated to the essential loops in the surface are elements of the cluster algebra. This is shown by exhibiting certain identities in the cluster algebra, that allow us to write the Laurent polynomials in question as polynomials in cluster variables. The main ingredients for the proof of these identities are the snake graph calculus developed in Reference CSReference CS2Reference CS3, and the skein relations proved in Reference MW.
1.2. Upper cluster algebras
As an application, we study the relationship between cluster algebras and upper cluster algebras. To define a cluster algebra , one needs to specify an initial seed consisting of a cluster and an exchange matrix . In Reference BFZ, the authors introduced the concept of the upper cluster algebra associated to the seed . Recall that consists of all elements of the ambient field which are Laurent polynomials over in the cluster variables from any seed in . It follows directly from the Laurent phenomenon that the upper cluster algebra contains the cluster algebra as a subalgebra. However, the question of whether the cluster algebra is equal to the upper cluster algebra is subtle and does not have a uniform answer. Already in Reference BFZ it is shown that for all acyclic types and, on the other hand, for the rank 3 case given by the once-punctured torus. Muller introduced the notion of locally acyclic cluster algebras in Reference M2 and showed that for all locally acyclic types in Reference M3. It is shown in Reference MSp that cluster algebras of Grassmannians are locally acyclic, hence in this case. Goodearl and Yakimov announced that for double Bruhat cells Reference GY.
For cluster algebras of finite mutation type, the following results are known:
- (1)
in the following types:
- -
surfaces with non-empty boundary and at least two marked points. This has been shown in Reference MSW2 for unpunctured surfaces, and in Reference M2 if at least two marked points are on the boundary. The case where only one point is on the boundary can be reduced to the case with two marked points on the boundary using the Louise property of Reference MSp; see Proposition 12.
- -
the exceptional types , by Reference BFZ, since these types are acyclic.
- -
the exceptional types and , by Reference M, since they are locally acyclic, or by Reference MSp, since they satisfy the Louise property.
- (2)
in the following types:
- -
surfaces without boundary and with exactly one puncture. This has been shown for the torus in Reference BFZ and for higher genus in Reference Lad.
- -
the exceptional type , Reference M4.
As an application of Theorem 2, we prove in Theorem 5 that
for surfaces without punctures and exactly one marked point.
This leaves the question open only for surfaces without boundary and at least two punctures.
Summarizing, we have the following result.
For all unpunctured surfaces, the cluster algebra is equal to the upper cluster algebra.
1.3. Maximal green sequences
Let be a quiver and let be the quiver obtained from by adding a vertex and an arrow , for each vertex of . The original vertices of are called unfrozen (or mutable) and the new vertices are called frozen. A green sequence is a sequence of mutations starting at such that at each step the mutation is performed at an unfrozen vertex , for which there is no arrow , from a frozen vertex . A green sequence is maximal if it produces a quiver which does not contain such a vertex .
Maximal green sequences have been introduced in Reference K. They are related to quantum dilogarithm identities, DT invariants and BPS states; see Reference BDP and the references therein.
The question of whether or not there exists a quiver in the mutation class of which admits a maximal green sequence seems related to the question of whether or not . Indeed, given a surface which is either a surface with boundary, or a sphere with at least four punctures, or a torus with at least two punctures, there exists a triangulation whose quiver admits a maximal green sequence. This has been shown in Reference ACCERV; see also Reference BDP for the sphere. Moreover, for all the exceptional types except for there exists a quiver that admits a maximal green sequence Reference ACCERV, whereas the mutation class does not contain a quiver that admits a maximal green sequence Reference Se.
On the other hand, it is shown in Reference BDP, Proposition 8.1 that if admits a non-degenerate potential such that the Jacobian algebra is infinite dimensional, then does not admit maximal green sequences. Combining this result with Reference GLS, Proposition 9.13, we see that quivers from closed surfaces with exactly one puncture do not admit maximal green sequences. The question seems to be open for closed surfaces of genus at least 2 and with at least two punctures.
Beyond finite mutation type, explicit maximal green sequences are announced by Yakimov for double Bruhat cells.
In all the known cases, maximal green sequences exist if and only if the cluster algebra is equal to the upper cluster algebra. Our Theorem 5 confirms this observation for unpunctured surfaces with exactly one marked point.
2. Main result
Let be a cluster algebra of an unpunctured surface with marked points whose coefficient system is such that the initial exchange matrix has maximal rank. The main result of Reference MSW2 is the construction of two bases for under the assumption that the number of marked points is at least two. These are the bangles basis and the bracelet basis . The assumption that the number of marked points is at least two was used in Reference MSW2 only to show that all elements of and are actually inside the cluster algebra, and not only in the upper cluster algebra. The proof of the spanning property and of linear independence does not rely on the number of marked points.
The following theorem removes the assumption on the number of marked points.
Let be the cluster algebra of an unpunctured surface with exactly one marked point and with arbitrary coefficients. Then both and are bases of the cluster algebra .
For the proof of this theorem, we need the following two lemmas. An essential loop in the surface is a closed curve in which is disjoint from the boundary of , which is not contractible and does not have any self-crossings. Since , the surface has exactly one boundary component. In Reference MSW2, the authors associate to every essential loop a Laurent polynomial given as a sum over perfect matchings of the corresponding band graph.
The Laurent polynomial of the essential loop around the boundary is in the cluster algebra .
The Laurent polynomial of every essential loop is in the cluster algebra .
Of course the second lemma implies the first, but the first is needed in the proof of the second. We prefer stating them separately, because their proofs use different techniques. The proof of Lemma 3 is given in Section 3 and the proof of Lemma 4 in Section 4.
Let be a triangulation of the surface and let be the associated exchange matrix. Since there are no punctures and the unique boundary component has an odd number of marked points (namely one), it follows from Reference FST, Theorem 14.3 that the rank of the matrix is maximal for every coefficient system. Therefore the results of Reference MSW2 show that both and are linearly independent and that every element of is a linear combination of elements of and also a linear combination of elements of .
It remains to show that and are subsets of .
Lemma 4 implies that every element of is in . Moreover the Laurent polynomials associated to the bracelets in can be written as Chebyshev polynomials in the Laurent polynomials associated to the essential loops in ; see Reference MSW2, Proposition 4.2. Thus is also a subset of .
■The following result follows directly from Theorem 2.
Let be the cluster algebra of an unpunctured surface with exactly one marked point and with trivial coefficients, and let be its upper cluster algebra. Then
It follows from Reference FG1, Theorem 12.3(ii) that is a basis of . Theorem 2 implies that , and thus . The other inclusion always holds.
■3. Proof of Lemma 3
We prove the lemma first for genus 1, then genus 2 and then for higher genus. Throughout the section, we denote by the cluster algebra with principal coefficients in the initial seed corresponding to our triangulation and by a cluster algebra with arbitrary coefficient system and initial seed corresponding to . More precisely, let be the tropical semifield and the initial coefficient tuple consisting of the generators of . Then is the cluster algebra with initial seed . On the other hand, let be any semifield and any coefficient tuple, thus . Then is the cluster algebra with initial seed .
Recall that every arc or loop in corresponds to a snake or band graph and to a Laurent polynomial given by perfect matchings of the snake or band graph. A band graph is obtained from a snake graph by identifying an edge in the first tile with an edge in the last tile. In the figures, this identification is represented by marking the vertices of the identified edges with bullets. For precise definitions, we refer to Reference MSW2. For the snake graph calculus used in this section, see Reference CS2.
3.1. Genus 1
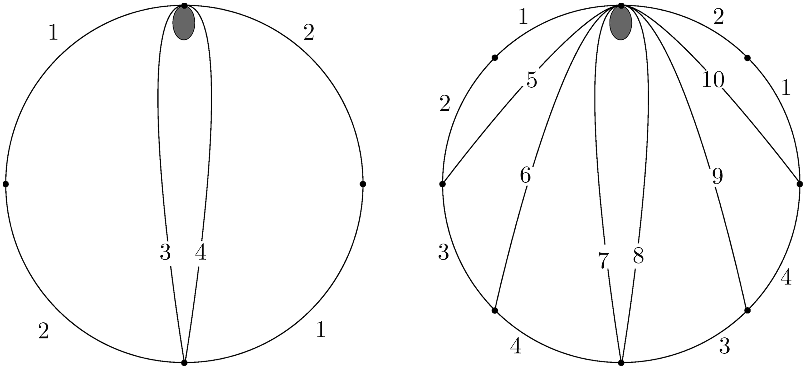
Let be a surface of genus 1 with one boundary component and one marked point. This case is known in the literature as ‘the dreaded torus’, because, among cluster algebras of surface type, it was the smallest example where the question of whether the cluster algebra is equal to the upper cluster algebra was open; see Reference MM, Remark 7.2.3. Fix the triangulation shown on the left in Figure 1, and let be the corresponding cluster in .
Let be the Laurent polynomial associated to the loop around the boundary. Its band graph is the first graph in the second row in Figure 2.
.
Let be the cluster variable given by the arc that starts at the marked point in the direction between the arc 3 and the boundary and then crosses the arcs in order and ends at the same marked point as it started from in the direction between the arc 3 and the boundary. Let be the cluster variable given by the symmetric arc, that is, the arc that starts at the marked point in the direction between the arc 4 and the boundary and then crosses the arcs in order and ends at the same marked point as it started from in the direction between the arc 4 and the boundary. The snake graphs of these two cluster variables are the first two snake graphs in the top row of Figure 2. The first two equations in that figure use snake graph calculus of Reference CS and Reference CS2 to compute the product showing that
where is the Laurent polynomial defined by the corresponding band graph in the figure. The first equation is the resolution of the grafting operation Reference CS, section 2.5, case 2 and the second equation is the resolution of three self-grafting operations Reference CS2, section 3.4. The graphs of and are band graphs.
Thus in order to show that it suffices to show that . This is done in the second computation in Figure 2, where we compute the product of the two cluster variables given by the arcs that cross and respectively, showing that
where is the Laurent polynomial defined by the corresponding snake graph in the figure. One can show that are cluster variables by checking that the associated arcs in the surface do not have a self-crossing, or by using Reference CS2 to show that their associated snake graphs do not have any self-crossing overlap. The first equation in this computation is the resolution of a grafting, the second equation is a self-grafting Reference CS2, section 3.3 and the third is a grafting of a band graph with a single edge Reference CS3 producing , as well as a self-grafting to obtain . Note that is a cluster variable corresponding to the arc crossing 3 and 4. This shows that . Since is an element of the group , its inverse is also in , and therefore , and thus .
■.
Using Fomin-Zelevinsky’s separation of addition formula Reference FZ4, Theorem 3.7 we see that the elements of can be computed from the elements in by replacing the principal coefficients by the corresponding and by dividing by the -polynomial evaluated over in . For example,
where
Evaluating the expressions in equations (Equation 1) and (Equation 2) in clearly preserves the identities. Then multiplying with the -polynomials we get
From equation (Equation 4) we see that , and since , and thus , this also implies that . Now equation (Equation 3) implies that , and, since , this shows that
■3.2. Genus 2
Let be a surface of genus 2 with one boundary component and one marked point. Fix the triangulation shown on the right in Figure 1, and let be the corresponding cluster in .
Let be the Laurent polynomial associated to the loop around the boundary. Its band graph is the first graph in the last row in Figure 3.
.
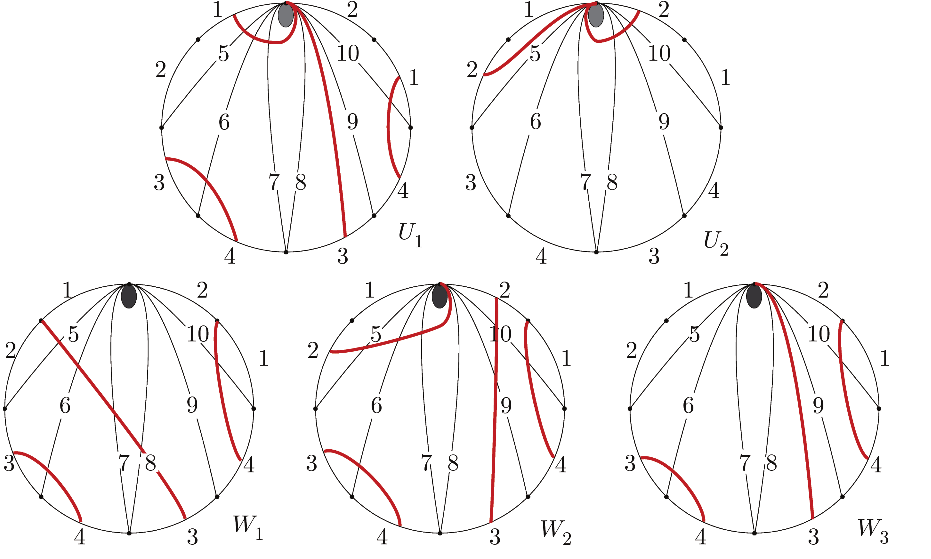
Let be the cluster variable obtained from by the mutation sequence , and let be the cluster variable obtained from by the mutation sequence . Then is the cluster variable corresponding to the arc that crosses and is the cluster variable corresponding to the arc that crosses . The corresponding snake graphs and are illustrated on the left-hand side of the equation in Figure 3.
Let be the Laurent polynomial defined by the band graph obtained from , for , by deleting the first and the last tile and then glueing. These band graphs are illustrated in the last row of Figure 3.
A simple computation using snake graph calculus shows that
This computation is given in Figure 3. The first equation is the resolution of a grafting, and the second is the resolution of three self-graftings.
In order to show that , it suffices to show that and are in the cluster algebra and, by symmetry, it is enough to show that is.
Let and be the Laurent polynomials associated to the snake graphs on the left-hand side of the equation in Figure 4. It follows from Reference CS2 that none of these two snake graphs has a self-crossing, which implies that and are cluster variables. Alternatively, we can see that and are cluster variables since each corresponds to an arc in the surface; see Figure 5. Indeed, the variable corresponds to the arc starting from the marked point into the triangle with sides , then crossing in order the arcs and ending at the marked point coming from the triangle with sides , where denotes the boundary segment; and the variable corresponds to the arc starting from the marked point into the triangle with sides , then crossing in order the arcs and ending at the marked point coming from the triangle with sides . Since these two curves do not have self-crossings, they are indeed arcs, and hence and are cluster variables.
Another simple calculation using snake graph calculus shows that
where the are cluster variables, and their corresponding arcs are illustrated in Figure 5. The computation is shown in Figure 4. The first equality in that figure is obtained by the grafting operation Reference CS2, section 2.9, case 2, the second equation by the self-grafting operation Reference CS2, section 3.4, and in the last equation the first two terms are obtained by grafting with a single edge Reference CS2, section 3.3, case 3 and the third and fourth term by self-grafting.
This shows that and hence that .
■.
The proof is exactly the same as in the genus 1 case.
■3.3. Higher genus
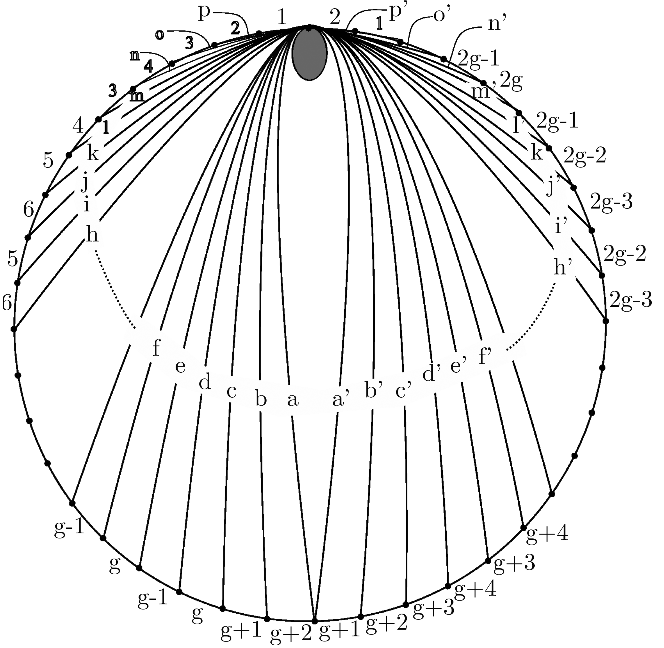
In this section, let be a surface of genus with one boundary component and one marked point. Fix the triangulation shown in Figure 6, and let be the corresponding cluster in . Note that the figure is for an even integer, but the case where is odd is similar; only the labeling changes slightly.
As in the genus 1 and 2 cases, let be the Laurent polynomial associated to the loop around the boundary.
.
The proof is an adaptation of the genus 2 argument. The cluster variables and are now given by the zigzag snake graphs shown in Figure 7. The Laurent polynomials , are again given by the band graphs obtained from the snake graphs of and by deleting the first and the last tile and then glueing. Again snake graph calculus shows that
where is a monomial in .
Finally to show that , and hence , is in the cluster algebra, we use the cluster variables analogous to the genus 2 case to get
This shows that and we are done.
■.
The proof is exactly the same as in the genus 1 case.
■4. Proof of Lemma 4
Let be an essential loop and let be the Laurent polynomial associated to it. In view of Lemma 3 we may suppose that is not the loop around the boundary. The proof uses a geometric argument with skein relations, and the relevant curves are illustrated in Figure 8. Choose a point on and a simple curve that goes from the marked point to the point . Let be the arc obtained by the curve . Let be the generalized arc that starts at the marked point, goes around the boundary twice and then ends at the marked point. The curves and are illustrated in the first row of Figure 8. Let and be the corresponding Laurent polynomials.
We compute the product using skein relations. Thus each equation is obtained by smoothing a crossing of the curves. This computation is illustrated in the second and third row of Figure 8. The first term on the right-hand side of the equation in the second row is a cluster variable given by the blue arc (the red arc is the boundary segment ) and the second term on the right-hand side still has a self-crossing. Applying the skein relations to that self-crossing produces the third row in the figure. In this row all red and green curves are boundary segments. Thus we get
where are some monomials in and and are cluster variables. Thus in order to show that , it suffices to show that . But it is shown in the last row of Figure 8 that , where (in blue) is the essential loop around the boundary. Now the result follows from Lemma 3.■
5. Punctured surfaces with boundary
In this section, we show how to reduce the case of punctured surfaces with exactly one marked point on the boundary to the case of surfaces with two marked points on the boundary.
Let be a punctured surface with boundary and one marked point on the boundary. Let be its cluster algebra and the corresponding upper cluster algebra.
.
By Reference MSp it suffices to show that there is a triangulation whose quiver satisfies the Louise property. Let be the marked point on the boundary and let be a puncture. Let be two arcs going from to and let be the arc from to going around the puncture such that cuts the surface into two pieces, one of which contains the boundary, the puncture and no other punctures; see the picture on the left-hand side of Figure 9. If the genus of is zero and is the only puncture, then the cluster algebra is of type and .
Otherwise, is not contractible, hence an arc, and we can choose a triangulation containing the arcs . Then in the corresponding quiver the vertices and are sinks or sources. Now the quiver obtained by removing the vertices and from the quiver is the same as the quiver of the triangulation obtained by deleting the arcs and of the surface obtained by replacing the puncture by a second point on the boundary; see the picture on the right-hand side of Figure 9. By induction, is Louise since has two boundary points and one puncture less than .
■Acknowledgements
Part of this work was carried out at the Centre de Recherche Mathématiques in Montréal, and the authors thank the CRM for their hospitality. The authors also thank Greg Muller for stimulating discussions.