PDFLINK |
Trapped Surfaces, Topology of Black Holes, and the Positive Mass Theorem
Communicated by Notices Associate Editor Daniela De Silva

1. Introduction
Albert Einstein’s theory of general relativity, first published in 1915, successfully unified special relativity with gravity and led to many predictions that have since been verified, marking one of the greatest triumphs of 20th century physics. Perhaps one of the most sensational features of the theory is the concept of a black hole—a region from which even light cannot escape. But what is a black hole, precisely? Do black holes really exist in nature? What do black holes have to do with mathematics?
This computer-simulated image shows a supermassive black hole at the center of a galaxy. The black region represents a snapshot of the event horizon of the black hole. Light from background stars is stretched and distorted due to the strong gravity of the black hole.

These questions and others have been pondered by generations of researchers. The 2020 Nobel Prize in Physics was awarded to mathematical physicist Roger Penrose for his “discovery that black hole formation is a robust prediction of the general theory of relativity,” and to astrophysicists Reinhard Genzel and Andrea Ghez for their “discovery of a supermassive compact object at the centre of our galaxy.” Although the very first nontrivial solution to Einstein’s equations ever discovered—the Schwarzschild spacetime—describes a black hole, many physicists, including Einstein, believed that black hole regions might only be present in highly symmetric solutions that were not realistic enough to describe nature. Penrose’s seminal 1965 paper Pen65 implied that the singular behavior associated with black holes persists even without symmetry, which was enough to convince many that black hole formation was a real physical phenomenon. But perhaps just as importantly, Penrose revolutionized the study of general relativity by introducing global differential geometric and topological methods, in contrast to the more calculation-based approaches of the past.
Also starting in the 1960s, the study of quasars eventually led astrophysicists to hypothesize that there were black holes at the centers of most galaxies, including our own galaxy, the Milky Way. It is difficult to directly observe something that cannot emit light, but starting in the 1990s, separate teams led by Genzel and Ghez began making detailed observations of the movements of stars near the center of the Milky Way, and after decades of collecting increasingly accurate data, we can now be confident that those movements are consistent with the existence of a black hole whose mass is 4.3 million times that of our Sun EG96GKMB98. See Figure 2.
The W. M. Keck Observatory is a two-telescope astronomical observatory near the summit of Mauna Kea in Hawaii. Starting in the 1990s, Ghez and her team used these telescopes and adaptive optics systems to track multiple stars orbiting the center of our galaxy.

Even more recently, in 2019, the Event Horizon Telescope—an international collaboration linking radio telescopes across the globe—treated us to spectacular pictures of the black hole (or rather, the “shadow” created by it) at the heart of Messier 87, an elliptical galaxy 55 million light-years from Earth. See Figure 3.
This image shows the elliptical galaxy Messier 87. The right top inset gives a close-up of two shockwaves created by a jet emanating from the galaxy’s supermassive black hole. The right bottom inset shows an image of that black hole produced by the Event Horizon Telescope Eve19.

In this article we provide an exposition of Penrose’s groundbreaking concepts of trapped surfaces and marginally outer trapped surfaces (MOTS), and some of their applications. Specifically, we will discuss Stephen Hawking’s result on the topology of black holes and some recent developments on the positive mass theorem that go back to the work of Richard Schoen and Shing-Tung Yau. The study of MOTS gives an effective way to understand some properties of black holes and turns out to have many analogies with the study of minimal surfaces. The theory of minimal surfaces is a mathematically rich topic with a long history that goes back to Lagrange’s work in the 18th century. Minimal surfaces also have many applications to such diverse fields as architecture, biology, and engineering, in addition to general relativity. See Figure 4. Exploring the intriguing connections between MOTS and minimal surfaces has led to fruitful developments in both general relativity and differential geometry.
Left: The roof of the Denver International Airport is a tensioned fabric structure that employs double-curved minimal surfaces. Right: Triply periodic minimal surfaces are used in industry as cost-effective functional components to produce high-complexity customized structures via 3D printing technology.

2. Trapped Surfaces
In this article our basic setting is a -dimensional spacetime, representing one time dimension and three spatial dimensions, and since we would like to describe an (effectively) isolated gravitational system, such as a galaxy, we assume that this spacetime is asymptotic to the trivial flat spacetime, which is usually called the Minkowski spacetime, near “infinity.” A rigorous general mathematical definition of a black hole is quite technical, but roughly speaking, when we refer to the black hole region of a spacetime, we mean a region that has the property that light rays emanating from the black hole region can never reach its complement, while from every point of the complement, one should be able to “escape to infinity” by following a light ray. The boundary of the black hole region is called the event horizon. Given a spatial -dimensional “snapshot in time” in our spacetime, we would like to understand which points in lie inside the black hole, but unfortunately, since the black hole region can only be technically defined in terms of global properties of the spacetime, it is impossible to tell whether or not a given point in lies inside the black hole without complete knowledge of the long-term spacetime future of .
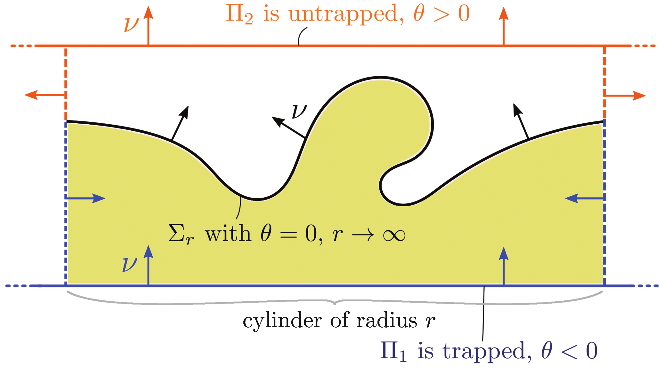
Penrose’s concept of a trapped surface offers us an accessible way to understand the location of a black hole without knowing its long-term future: Given a -surface in spacetime, imagine shooting a light ray from each point of , and then define to be the surface obtained by following these light rays for parameter-time , so that can be thought of as a “shell of light” emanating from . (Note that we should not think of this as actual “time” since light does not experience passage of time.) We typically expect that if we shoot these light rays inward, the area of will decrease in , and that if we shoot them outward, the area of will increase, as is the case for a standard sphere in the Minkowski spacetime. However, in the presence of strong gravity, it is possible for the family of outgoing light shells to have decreasing area forms at each point of , and in this case we say that is an (outer) trapped surface. See Figure 5. Meanwhile, a marginally outer trapped surface (or MOTS) refers to the borderline case in which the area forms at each point are unchanging to first-order in .
Typically, the outgoing “light shell” has increasing area form as it exits the surface, as shown for the surface . Meanwhile, for the trapped surface , the area form is decreasing.

Penrose’s famed singularity theorem states that under certain physically reasonable assumptions, the existence of a closed trapped surface implies that there is a light ray emanating from the trapped surface that eventually runs into a singularity. Intuitively, the behavior of a trapped surface feels a bit like saying that even though the light rays are “directed outward,” they are still “moving inward,” which vaguely captures the idea of light not being able to “escape.” Because of this heuristic and Penrose’s singularity theorem, physicists often associate trapped surfaces with the existence of black holes, and in fact, under certain global hypotheses, one can even prove that trapped surfaces must lie inside the black hole region. Because of this relationship, the (weakly) trapped region of , which we define to be the region of enclosed by either trapped surfaces or MOTS in , can be thought of as a simpler stand-in for the intersection of with the black hole region, and the apparent horizon of , which we define to be the boundary of the trapped region of , can be thought of as a simpler stand-in for the intersection of with the event horizon. The advantage of these concepts is that the trapped region and apparent horizon are entirely determined by data along the spatial 3-dimensional “snapshot in time” .
3. Spacetime Geometry
Since we want to consider -dimensional spacetimes but without a uniquely determined “time coordinate,” the natural setting of general relativity is a -manifold. A Lorentzian metric on a -manifold defines an inner product with signature on each tangent space of , smoothly depending on the base point. This means that at each point of , there is an orthogonal basis of tangent vectors such that and for . So if a tangent vector is given by when written in this basis, then . If one thinks of Riemannian geometry as being locally modeled on the Euclidean metric , one can analogously think of Lorentzian geometry as being locally modeled on the Minkowski metric . Special relativity is essentially the physics of Minkowski geometry, so the reason why a Lorentzian manifold is the natural setting for general relativity is that the theory should be locally modeled on special relativity. Moreover, we will often implicitly assume that is asymptotic to the Minkowski metric in some sense.
At the tangent space of each point, one can define the future and past light cones. Two future null vectors and are given. The yellow curve is null as its tangent vector is null at each point. The submanifold at the bottom-right is spacelike because its tangent vectors are spacelike at each point.
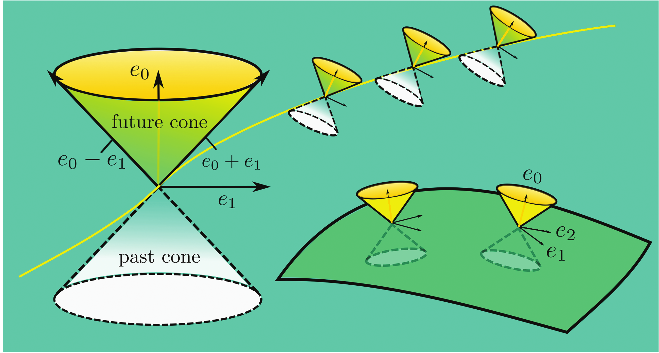
For any tangent vector of , we call it timelike if , null if , and spacelike if . So for example, is timelike, is spacelike, and is null. The null vectors form a double cone which separates the timelike vectors from the spacelike ones. A spacetime is a Lorentzian -manifold equipped with a globally defined unit timelike vector field, which we may select as our at every point. This choice allows us to further distinguish between future null or timelike vectors, which lie on or above the upper half of the null cone, and past null or timelike vectors, which lie on or below the lower half of the null cone.
A submanifold of is called spacelike if all of its tangent vectors are spacelike, or equivalently, if induces a Riemannian metric on it. In particular, we define a spacelike slice of to be a -dimensional spacelike hypersurface , which is what we earlier referred to as a “snapshot in time.” The induced Riemannian metric and the second fundamental formFootnote1 of a spacelike slice can largely capture the spacetime geometry along , and we will refer to as an initial data set. A curve is called null (or timelike) if its tangent vector is null (or timelike) at each point. See Figure 6. As in Riemannian geometry, a Lorentzian metric gives us a concept of “straight lines,” which we call geodesics. The path of a light ray traces out a future null geodesic in the spacetime, while a massive test particle will trace out a future timelike geodesic. A test particle that traces out a spacelike geodesic would travel faster than the speed of light, and thus it is unphysical.
The second fundamental form of is defined to be the tangential part of where is the future unit normal of .
The Schwarzschild metric in the ingoing Eddington-Finkelstein coordinates (one space dimension suppressed). Any light ray that starts at a point where will crash into the singularity. The surfaces defined by constant coordinates are trapped surfaces whenever , and they are MOTS when .

Einstein’s equations demand that certain “curvatures” of must be equal to the stress-energy tensor, which describes the distribution of energy in the spacetime.Footnote2 One can view these equations as a complicated nonlinear system of partial differential equations on , with the stress-energy tensor as a source term. An initial data set may be regarded as Cauchy data for this system of partial differential equations, as explicated by the fundamental work of Yvonne Choquet-Bruhat on well-posedness of the Einstein equations.
Specfically, the curvatures referred to here are the Einstein tensor of , defined to be where and are the Ricci and scalar curvatures of , respectively.
As alluded to earlier, the Schwarzschild metrics were the first nontrivial solutions to be discovered with source term equal to zero. In one particular choice of coordinates, the Schwarzschild metric of mass can be written as
which is a smooth Lorentzian metric on , where , , and is the standard Riemannian metric on the sphere . In this spacetime, one can show that a light ray emanating from within the region can never enter the region , while any point in the region can be connected to “infinity” by a light ray. Or in other words, the region is a black hole region, with its boundary as the event horizon. It is also a fact that as approaches zero, the metric becomes singular there in the sense that the curvature blows up, and moreover, any light ray (or massive test particle) starting at a point where will inevitably crash into this singularity. See Figure 7.
4. Variations of Surface Area
Earlier we described trapped surfaces in terms of decreasing area forms of “light shells.” Here we will make that precise, but first we discuss the simpler concept of varying the area form of a surface in a Riemannian -manifold . Suppose is a unit normal vector on , which we will regard as the “outward” direction (regardless of whether separates into an “outside” and “inside”), and let be a family of diffeomorphisms on with equal to the identity. Then defines a family of surfaces, sometimes called variations of , whose first-order variation vector field along is defined by for each
One simple variation of
Parallel surfaces of distance
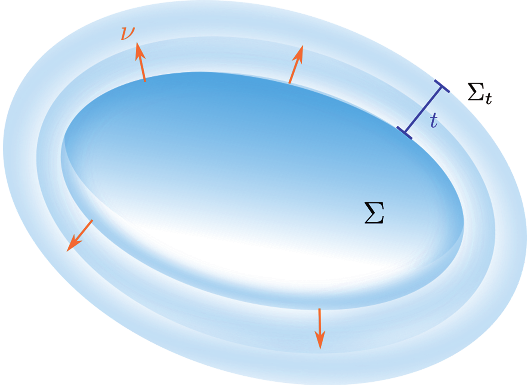
These are called parallel surfaces because
at each
One can then show that for any outward normal variation with first-order variation
Now consider a spacelike
Define a family
at each
Now suppose that the
5. Topology of Black Holes
Going back to the example of the Schwarzschild spacetime, each choice of
A spacetime is called stationary if it admits a global Killing vector field that is asymptotically timelike.
Let
Any orientable locally outermost closed MOTS in an initial data set satisfying the dominant energy condition must be a topological sphere.
The dominant energy condition is a physically realistic assumption on the stress-energy tensorFootnote4, which we will come back to later. This result was generalized by Gregory Galloway and Schoen, who showed that higher dimensional analogues of apparent horizons must be topologically Yamabe positive GS06.
Explicitly, we say that an initial data set
6. The Locally Outermost Property
Schoen and Yau were the first to notice that minimal surfaces could be used to study scalar curvature. The scalar curvature
While Hawking exploited the relationship between an outermost MOTS
Given a surface
Any orientable locally outermost closed minimal surface
Lawson’s minimal surfaces of genus

Let
for some constant
Routine geometric computations, including use of the Gauss equation, show that
where
and integrating this over
Therefore
To rule out the torus, suppose to the contrary that
Since
Without the locally outermost assumption, a minimal surface can have higher genus. For example, the standard 3-sphere admits closed minimal surfaces of arbitrary genus. See Figure 9. Over the last decade Fernando Marques and André Neves have advanced the study of minimal surfaces using min-max methods, and building on their work, Haozhao Li and Xin Zhou proved that a generic closed Riemannian
The proof of Theorem 1 is conceptually similar to that of Theorem 2. In that case, we start with an orientable locally outermost closed MOTS
for some quantity
7. Positive Mass Theorem
We will now discuss how a version of the topological argument from the previous section can be used to prove the celebrated positive mass theorem. Let
The ADM energy-momentum was formulated by physicists Arnowitt, Deser, and Misner, and explicitly, the numbers
Let
This is called the “positive mass theorem” because an object with future timelike energy-momentum
The positive mass theorem is highly desirable for physical reasons. The dominant energy condition can be described as the reasonable physical assumption that the sources for Einstein’s equations cannot travel faster than light, as measured by any observer. The positive mass theorem loosely asserts that as long as these sources cannot travel faster than light, the entire configuration of sources, as viewed from far away, should not behave like an object traveling faster than light, or as fast as light. An example of a violation of the positive mass theorem could be a configuration of positive mass sources that somehow repels far away objects instead of attracting them. Because of the nonlinearities of Einstein’s equations, it is highly nontrivial to prove that such perversities cannot happen.
The study of the positive mass theorem has a long history. A particularly important special case is when
Under the (contradictory) assumption
We outline the proof of the nonnegative mass theorem for 3-dimensional
By a subtle density theorem (see Section 6 of EHLS16), one can show that without loss of generality, we can assume that the “strict” dominant energy condition holds and that the initial data
The proof proceeds by contradiction. Suppose that
To prove the equality case of the positive mass theorem requires significant extra work. One must show that if
One curious feature of both our proof and the spinor proof is that in higher dimensions, the equality case of the positive mass theorem seems to require a stronger definition of asymptotic flatness than the standard one needed for the “nonnegative mass theorem” to be true. Somewhat surprisingly, it turns out that when the spatial dimension is greater than eight, there do exist counterexamples to the expected strict inequality
While Penrose’s advances were only recently honored by the Nobel Prize in Physics, the topological and geometric methods that he introduced helped to build a long, intimate relationship between mathematics and general relativity over the past several decades. We discussed groundbreaking work of Hawking, Schoen, and Yau as fine examples of the intriguing interactions between geometry, topology, analysis, and general relativity. New applications and interconnections between mathematics and general relativity are continually being discovered in more recent developments, as described above. For a more extensive introduction to this field of research, please see the recent graduate-level textbook by the second author Lee19. We expect that the exchange of ideas between physics and mathematics will continue to energize these directions of inquiry, which we have only lightly touched upon here. Penrose once stated, “We have a closed circle of consistency here: the laws of physics produce complex systems, and these complex systems lead to consciousness, which then produces mathematics, which can then encode in a succinct and inspiring way the very underlying laws of physics that gave rise to it.”
References
- [AEM11]
- Lars Andersson, Michael Eichmair, and Jan Metzger, Jang’s equation and its applications to marginally trapped surfaces, Complex analysis and dynamical systems IV. Part 2, Contemp. Math., vol. 554, Amer. Math. Soc., Providence, RI, 2011, pp. 13–45, DOI 10.1090/conm/554/10958. MR2884392Show rawAMSref
\bib{Andersson-Eichmair-Metzger:2011}{article}{ author={Andersson, Lars}, author={Eichmair, Michael}, author={Metzger, Jan}, title={Jang's equation and its applications to marginally trapped surfaces}, conference={ title={Complex analysis and dynamical systems IV. Part 2}, }, book={ series={Contemp. Math.}, volume={554}, publisher={Amer. Math. Soc., Providence, RI}, }, date={2011}, pages={13--45}, review={\MR {2884392}}, doi={10.1090/conm/554/10958}, }Close amsref.✖ - [BC96]
- Robert Beig and Piotr T. Chruściel, Killing vectors in asymptotically flat space-times. I. Asymptotically translational Killing vectors and the rigid positive energy theorem, J. Math. Phys. 37 (1996), no. 4, 1939–1961, DOI 10.1063/1.531497. MR1380882Show rawAMSref
\bib{Beig-Chrusciel:1996}{article}{ author={Beig, Robert}, author={Chru\'{s}ciel, Piotr T.}, title={Killing vectors in asymptotically flat space-times. I. Asymptotically translational Killing vectors and the rigid positive energy theorem}, journal={J. Math. Phys.}, volume={37}, date={1996}, number={4}, pages={1939--1961}, issn={0022-2488}, review={\MR {1380882}}, doi={10.1063/1.531497}, }Close amsref.✖ - [CH20]
- Justin Corvino and Lan-Hsuan Huang, Localized deformation for initial data sets with the dominant energy condition, Calc. Var. Partial Differential Equations 59 (2020), no. 1, Paper No. 42, 43, DOI 10.1007/s00526-019-1679-9. MR4062040Show rawAMSref
\bib{Corvino-Huang:2020}{article}{ author={Corvino, Justin}, author={Huang, Lan-Hsuan}, title={Localized deformation for initial data sets with the dominant energy condition}, journal={Calc. Var. Partial Differential Equations}, volume={59}, date={2020}, number={1}, pages={Paper No. 42, 43}, issn={0944-2669}, review={\MR {4062040}}, doi={10.1007/s00526-019-1679-9}, }Close amsref.✖ - [EG96]
- A. Eckart and R. Genzel, Observations of stellar proper motions near the galactic centre, Nature 383 (1996), no. 6599, 415–417.Show rawAMSref
\bib{Genzel}{article}{ author={Eckart, A.}, author={Genzel, R.}, title={Observations of stellar proper motions near the galactic centre}, date={1996}, journal={Nature}, volume={383}, number={6599}, pages={415\ndash 417}, url={https://doi.org/10.1038/383415a0}, }Close amsref.✖ - [Eic09]
- Michael Eichmair, The Plateau problem for marginally outer trapped surfaces, J. Differential Geom. 83 (2009), no. 3, 551–583. MR2581357Show rawAMSref
\bib{Eichmair:2009JDG}{article}{ author={Eichmair, Michael}, title={The Plateau problem for marginally outer trapped surfaces}, journal={J. Differential Geom.}, volume={83}, date={2009}, number={3}, pages={551--583}, issn={0022-040X}, review={\MR {2581357}}, }Close amsref.✖ - [EHLS16]
- Michael Eichmair, Lan-Hsuan Huang, Dan A. Lee, and Richard Schoen, The spacetime positive mass theorem in dimensions less than eight, J. Eur. Math. Soc. (JEMS) 18 (2016), no. 1, 83–121, DOI 10.4171/JEMS/584. MR3438380Show rawAMSref
\bib{Eichmair-Huang-Lee-Schoen:2016}{article}{ author={Eichmair, Michael}, author={Huang, Lan-Hsuan}, author={Lee, Dan A.}, author={Schoen, Richard}, title={The spacetime positive mass theorem in dimensions less than eight}, journal={J. Eur. Math. Soc. (JEMS)}, volume={18}, date={2016}, number={1}, pages={83--121}, issn={1435-9855}, review={\MR {3438380}}, doi={10.4171/JEMS/584}, }Close amsref.✖ - [Eve19]
- Event Horizon Telescope Collaboration, First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole, ApJL 875 (April 2019), no. 1, L1, available at 1906.11238.Show rawAMSref
\bib{EHT}{article}{ author={{Event Horizon Telescope Collaboration}}, title={{First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole}}, date={2019-04}, journal={ApJL}, volume={875}, number={1}, pages={L1}, eprint={1906.11238}, }Close amsref.✖ - [GS06]
- Gregory J. Galloway and Richard Schoen, A generalization of Hawking’s black hole topology theorem to higher dimensions, Comm. Math. Phys. 266 (2006), no. 2, 571–576, DOI 10.1007/s00220-006-0019-z. MR2238889Show rawAMSref
\bib{Galloway-Schoen:2006}{article}{ author={Galloway, Gregory J.}, author={Schoen, Richard}, title={A generalization of Hawking's black hole topology theorem to higher dimensions}, journal={Comm. Math. Phys.}, volume={266}, date={2006}, number={2}, pages={571--576}, issn={0010-3616}, review={\MR {2238889}}, doi={10.1007/s00220-006-0019-z}, }Close amsref.✖ - [GKMB98]
- A. M. Ghez, B. L. Klein, M. Morris, and E. E. Becklin, High Proper-Motion Stars in the Vicinity of Sagittarius A*: Evidence for a Supermassive Black Hole at the Center of Our Galaxy, ApJ 509 (December 1998), no. 2, 678–686, available at astro-ph/9807210.Show rawAMSref
\bib{Ghez}{article}{ author={{Ghez}, A.~M.}, author={{Klein}, B.~L.}, author={{Morris}, M.}, author={{Becklin}, E.~E.}, title={{High Proper-Motion Stars in the Vicinity of Sagittarius A*: Evidence for a Supermassive Black Hole at the Center of Our Galaxy}}, date={1998-12}, journal={ApJ}, volume={509}, number={2}, pages={678\ndash 686}, eprint={astro-ph/9807210}, }Close amsref.✖ - [GHHP83]
- G. W. Gibbons, S. W. Hawking, Gary T. Horowitz, and Malcolm J. Perry, Positive mass theorems for black holes, Comm. Math. Phys. 88 (1983), no. 3, 295–308. MR701918Show rawAMSref
\bib{GHHP}{article}{ author={Gibbons, G.~W.}, author={Hawking, S.~W.}, author={Horowitz, Gary~T.}, author={Perry, Malcolm~J.}, title={Positive mass theorems for black holes}, date={1983}, issn={0010-3616}, journal={Comm. Math. Phys.}, volume={88}, number={3}, pages={295\ndash 308}, url={http://projecteuclid.org.queens.ezproxy.cuny.edu/euclid.cmp/1103922377}, review={\MR {701918}}, }Close amsref.✖ - [Haw72]
- S. W. Hawking, Black holes in general relativity, Comm. Math. Phys. 25 (1972), 152–166. MR293962Show rawAMSref
\bib{Hawking:1972}{article}{ author={Hawking, S. W.}, title={Black holes in general relativity}, journal={Comm. Math. Phys.}, volume={25}, date={1972}, pages={152--166}, issn={0010-3616}, review={\MR {293962}}, }Close amsref.✖ - [Haw73]
- S. W. Hawking, The event horizon, Les Houches Summer School of Theoretical Physics: Black Holes, 1973.Show rawAMSref
\bib{Hawking:1973}{inproceedings}{ author={Hawking, S.~W.}, title={{The event horizon}}, date={1973}, booktitle={{Les Houches Summer School of Theoretical Physics}: {Black Holes}}, }Close amsref.✖ - [HL20a]
- Lan-Hsuan Huang and Dan A. Lee, Bartnik mass minimizing initial data sets and improvability of the dominant energy scalar, arXiv:2007.00593 [math.DG], 2020.Show rawAMSref
\bib{Huang-Lee:2021}{eprint}{ author={Huang, Lan-Hsuan}, author={Lee, Dan~A.}, title={{B}artnik mass minimizing initial data sets and improvability of the dominant energy scalar}, date={2020}, arxiv={2007.00593 [math.DG]}, }Close amsref.✖ - [HL20b]
- Lan-Hsuan Huang and Dan A. Lee, Equality in the spacetime positive mass theorem, Comm. Math. Phys. 376 (2020), no. 3, 2379–2407, DOI 10.1007/s00220-019-03619-w. MR4104553Show rawAMSref
\bib{Huang-Lee:2020}{article}{ author={Huang, Lan-Hsuan}, author={Lee, Dan A.}, title={Equality in the spacetime positive mass theorem}, journal={Comm. Math. Phys.}, volume={376}, date={2020}, number={3}, pages={2379--2407}, issn={0010-3616}, review={\MR {4104553}}, doi={10.1007/s00220-019-03619-w}, }Close amsref.✖ - [Lee19]
- Dan A. Lee, Geometric relativity, Graduate Studies in Mathematics, vol. 201, American Mathematical Society, Providence, RI, 2019. MR3970261Show rawAMSref
\bib{Lee:book}{book}{ author={Lee, Dan~A.}, title={Geometric relativity}, series={Graduate Studies in Mathematics}, publisher={American Mathematical Society, Providence, RI}, date={2019}, volume={201}, isbn={978-1-4704-5081-6}, url={https://doi-org.queens.ezproxy.cuny.edu/10.1090/gsm/201}, review={\MR {3970261}}, }Close amsref.✖ - [LLU21]
- Dan A. Lee, Martin Lesourd, and Ryan Unger, Density and positive mass theorems for initial data sets with boundary, arXiv:2112.12017 [math.DG], 2021.Show rawAMSref
\bib{Galloway-Lee:preprint}{eprint}{ author={Lee, Dan A.}, author={Lesourd, Martin}, author={Unger, Ryan}, title={Density and positive mass theorems for initial data sets with boundary}, date={2021}, arxiv={2112.12017 [math.DG]}, }Close amsref.✖ - [Pen65]
- Roger Penrose, Gravitational collapse and space-time singularities, Phys. Rev. Lett. 14 (1965), 57–59, DOI 10.1103/PhysRevLett.14.57. MR172678Show rawAMSref
\bib{Penrose:1965}{article}{ author={Penrose, Roger}, title={Gravitational collapse and space-time singularities}, journal={Phys. Rev. Lett.}, volume={14}, date={1965}, pages={57--59}, issn={0031-9007}, review={\MR {172678}}, doi={10.1103/PhysRevLett.14.57}, }Close amsref.✖ - [SY79]
- Richard Schoen and Shing Tung Yau, On the proof of the positive mass conjecture in general relativity, Comm. Math. Phys. 65 (1979), no. 1, 45–76. MR526976Show rawAMSref
\bib{Schoen-Yau:1979-pmt1}{article}{ author={Schoen, Richard}, author={Yau, Shing Tung}, title={On the proof of the positive mass conjecture in general relativity}, journal={Comm. Math. Phys.}, volume={65}, date={1979}, number={1}, pages={45--76}, issn={0010-3616}, review={\MR {526976}}, }Close amsref.✖ - [SY81]
- Richard Schoen and Shing Tung Yau, Proof of the positive mass theorem. II, Comm. Math. Phys. 79 (1981), no. 2, 231–260. MR612249Show rawAMSref
\bib{Schoen-Yau:1981-pmt2}{article}{ author={Schoen, Richard}, author={Yau, Shing Tung}, title={Proof of the positive mass theorem. II}, journal={Comm. Math. Phys.}, volume={79}, date={1981}, number={2}, pages={231--260}, issn={0010-3616}, review={\MR {612249}}, }Close amsref.✖ - [Wit81]
- Edward Witten, A new proof of the positive energy theorem, Comm. Math. Phys. 80 (1981), no. 3, 381–402. MR626707Show rawAMSref
\bib{Witten:1981}{article}{ author={Witten, Edward}, title={A new proof of the positive energy theorem}, journal={Comm. Math. Phys.}, volume={80}, date={1981}, number={3}, pages={381--402}, issn={0010-3616}, review={\MR {626707}}, }Close amsref.✖
Credits
Opening image is courtesy of NASA’s Goddard Space Flight Center; background, ESA/Gaia/DPAC.
Figure 1 is courtesy of NASA, ESA, and D. Coe, J. Anderson, and R. van der Marel (STScI).
Figure 2 is courtesy of Left_Coast_Photographer.
Figure 3 is courtesy of NASA/JPL-Caltech/IPAC/Event Horizon Telescope Collaboration.
Figure 4 (left) is courtesy of arinahabich via Getty.
Figure 4 (right) is courtesy of Julián Norato, adapted from ntopology.com.
Figures 5–8 and 10 are courtesy of Lan-Hsuan Huang.
Figure 9 is courtesy of Nick Schmitt.
Photo of Lan-Hsuan Huang is courtesy of Damin Wu.
Photo of Dan A. Lee is courtesy of Dan A. Lee.



