Games for Your Mind

Like many mathematicians, my favorite mathematical memory is associated with a particular puzzle. The date is March 14 (Pi Day, natch), and I was a graduate student at Auburn University. While you might first assume this event took place in an office or classroom, in this tale I’m yelling into a conference call on my cell phone as I drive as quickly as was legally allowed.

“Wait, what were those GPS coordinates again? Are you sure?” We had just finished solving “Pie Charts,” which involved cracking the code shown in Figure 1 (hint: use semaphore to reveal a 7-letter word). The ultimate solution was a particular set of GPS coordinates, but rather than leading to any particular landmark, they seemed to indicate the middle of a busy intersection.

Figure 1.

A “pi” chart logic puzzle.

It was still the relatively early hours of “Eric’s Circle of Friends,” the latest installment of mathematician and puzzle designer Eric Harshbarger’s annual “puzzle hunts.” In such events, competing teams of players are tasked with a sequence of fiendish puzzles involving logic, mathematics, wordplay, and more. Each solution in the hunt would lead to a particular location where a secret code was hidden. Reporting each code to Eric would award our team points, but as usual, we expected there was more to these locations and codes than met the eye.

After finding the code written on a sticker adhered to the walk signal at one corner of the intersection, I returned to my vehicle slightly frustrated and confused. Why would Eric have chosen such an arbitrary (yet precise) location? This was the second set of GPS coordinates we had used that day, which had struck me as odd. Usually, solutions were obvious landmarks or well-known buildings, but it seemed that this year, precision in positioning was a key factor in where solutions were located.

“Wait a second!” I exclaimed to my teammates on the call from back at Headquarters. “What happens if we plot these positions together on a map of town?”

I had just stumbled onto the first of several metapuzzles for the game. In his book Games for Your Mind, author Jason Rosenhouse notes that the term is attributed to prolific mathematician and puzzler Raymond Smullyan. In the classic sense, a metapuzzle is a written logic puzzle wherein the reader isn’t given all the clues directly, but instead is told which characters within the story have solved which pieces of the puzzle. By the end of the narrative, the characters have solved the puzzle, and by inferring what the characters (whom one presumes are perfect logicians) must have known to do so, the reader can come to the same conclusion on their own. Smullyan often enjoyed employing metapuzzle elements in his well-known Knight/Knave puzzles, and as a major topic of interest in the book under review, I enjoyed learning from Rosenhouse about the history of Knights and Knaves, which is much richer than I’d previously appreciated.

In the context of a puzzle hunt, players may be thought of as characters within such a story. We knew the solutions to three of four of the hunt’s “yellow” puzzles, and that the fourth solution would reveal a new challenge. But often such metapuzzles can be solved with partial information, and I had a hunch.

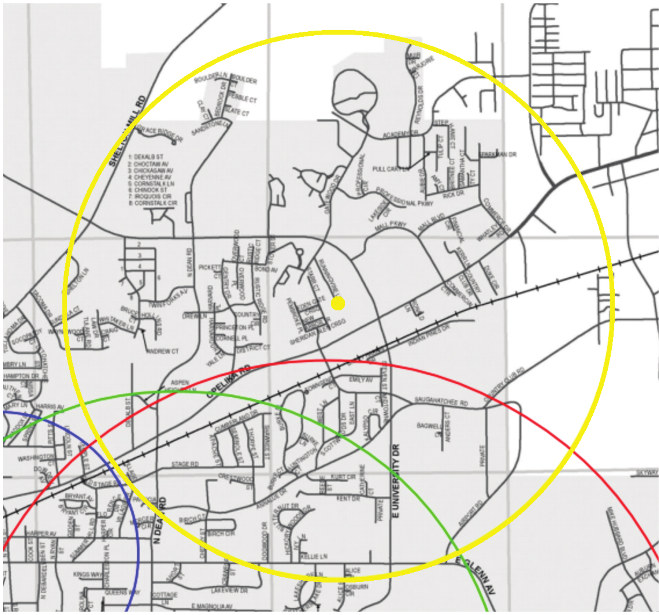
It’s well-known 2 that there exists a unique circle whose circumference passes through any three given non-colinear points. Of course, this assumes precise knowledge of these three locations, such as very specific GPS coordinates. Not every solution had led us to such exact locations, but what if we knew the fourth location? Hurrying back to Headquarters, I used an online graphing tool to model the three known locations as coordinates in the Euclidean plane, and constructed the center of the circle. With only a rough description for one of our three known locations, I had only vague confidence in my result, but as luck would have it, a teammate would soon report in, having just found the fourth location.

I scrambled to take the call, “Do you have a GPS app on your phone?” With the knowledge of the exact coordinates of the solution sticker, I confirmed that it also lay near the circumference I had found from the other three. I replaced the vague solution with this new precise one, to discover that the center of this circle was located neatly in the middle of a suburban cul-de-sac (Figure 2). Regrettably it made no sense for me to drive there myself; we had another teammate in the field who was much closer. Too anxious to work on another of our dozen or so unsolved puzzles, I waited for her call. Shortly, we received it. “Well folks, I’m here.” A pause. “There’s a package, and according to what’s written on it, it seems that we’ve just become part of ‘Eric’s Inner Circle of Friends.’”

Figure 2.

Partial map of a puzzle hunt metapuzzle.

The wave of epiphany I experienced in realizing the importance of these specific locations, and the mathematical connection with constructing circles in the plane, is likely familiar to most readers active in mathematics. We toil at blackboards, arguing with ourselves and colleagues, as we try to unearth mathematical truths. And once they become clear, often appearing so naturally, if not obviously, we similarly experience that sensation of realization. For a brief moment, we feel we understand, and many of us do mathematics in pursuit of that exhilaration. (As @TamasGorbe so eloquently put it in a May 2021 tweet, “mathematicians are bliss junkies.”) Of course, that feeling is fleeting, and so it’s onto the next puzzle.

For many of us, bottling this emotion and helping our students experience it for themselves is the crux of our outreach and pedagogy. Indeed, there’s a market for it. While puzzle hunts are still a niche experience (albeit a hobby that enthusiasts have been enjoying for decades), they provided inspiration for the more mainstream “Escape Room” experience 3. Briefly, one might describe an escape room as a condensed version of a puzzle hunt, constrained to a single hour and a single room, with the final goal of “escaping” the room by entering a code into a keypad locking the exit.

While my story above was a recollection of my actual puzzling experience, I did my best to tell it in the spirit of Dan Brown’s Da Vinci Code novel or one of Sir Arthur Conan Doyle’s tales of consulting detective Sherlock Holmes. Thrilling logical deductions are also a common trope in film and television, manifested by such characters as National Treasure’s Benjamin Franklin Gates and Knives Out’s Benoit Blanc; even Disney Junior’s Mira, Royal Detective has my daughter on the case. There are no shortage of video games that allow players to use logic and puzzle-solving to determine whodunit themselves, such as Professor Layton, Phoenix Wright: Ace Attorney, and more.

Setting aside these narrative experiences, even the simple exercise of solving a Sudoku or Calcudoku puzzle can allow general audiences to experience the feeling of revelation associated with mathematical epiphany. An example of Calcudoku (invented by Japanese schoolteacher Tetsuya Miyamoto, and also known by the “KenKen” brand name) is shown in Figure 3. The first requirement of a $5\times 5$ Calcudoku is that each cell of the grid be filled with a number between $1$ and $5$. It’s easy to explain to anyone that a Calcudoku requires that each row and column contain exactly one instance of each digit, but to a mathematician, this is a characterization of the so-called Latin square. Such configurations are studied by researchers of design theory, and can be used for nontrivial applications such as experimental design.

The second requirement is that each “cage” of cells enclosed by a bold boundary must have values that add, subtract, multiply, or divide to obtain the value clued in the corner of the cage. For example, a “$4-$” cage must contain “$1$” and “$5$” (in either order). While this may appear to be a trivial matter of arithmetic, advanced puzzles require reasoning about integer partitions and factorizations beyond the scope of most grade school classrooms. The interested reader may refer to 4 for more information on the logic of Calcudoku and its use in the classroom.

Figure 3.

A Calcudoku logic puzzle.

With such a rich and varied history of how mathematicians and the general public experience logic puzzles in games and media, the subtitle for Rosenhouse’s book, The History and Future of Logic Puzzles, has set itself a very high bar. And therein lies my largest disappointment with the text: it never actually attempts to be this promised exploration of logic puzzles past and future, at least not in general. Many readers may choose to pick up this book based on their interest in one or more of the aspects of puzzling I describe above, and indeed Princeton University Press anticipates this in the second sentence of the inside flap. “Games like Sudoku and Mastermind are fun and engrossing recreational activities, but they also share deep foundations in mathematical logic and are worthy of serious intellectual inquiry.” But other than a very brief interlude (portions of Chapter 2, “Logic Just for Fun“), Rosenhouse does not discuss such puzzles or their underlying mathematical foundations. Calcudoku (along with any other non-Western puzzle besides Sudoku) is absent from this text, and even the popular categorical logic puzzle genre (given these clues, which person lives in which house, owns which pet, and prefers which candy?) is limited to a single puzzle, despite its folklore attribution to Lewis Carroll, who is otherwise well-discussed.

As for the titular “future” of logic puzzles, little is said other than a brief suggestion in the book’s preface that it involves “crafting puzzles based on nonclassical logics.” Certainly, the author did not intend this as a claim concerning logic puzzles of all stripes. Indeed, the popularity of the Cracking the Cryptic YouTube channel, which features new variations on classical logic puzzles every week for its hundreds of thousands of subscribers, proves otherwise.

So one must then temper their expectations. If Games for Your Mind was never intended to be a comprehensive history of logic puzzles throughout the world, what is it attempting instead? Rosenhouse’s characterization of logic puzzles is focused on enigmas presented as narratives, and his book focuses primarily on the work of two particular logicians well-known for such puzzles. As a deep and thoughtful exploration of this proper subset of puzzling, along with its mathematical and logical foundations, the book is an informative and engaging read.

In the first main division of the book, “Lewis Carroll and Aristotelian Logic,” Rosenhouse first introduces us to Aristotle’s syllogism, which the book’s glossary defines as “an argument with two premises and a conclusion.” Take for instance the following.

•

No exams are neat.

•

All puzzles are neat.

What can one deduce? An equivalent puzzle we might present our mathematics students follows.

•

No circles are rectangles.

•

All squares are rectangles.

From these, we might hope our students can conclude that “no squares are circles.”

Rosenhouse dedicates a chapter to each of two works by Lewis Carroll related to such puzzles. Perhaps best-known as the author of Alice’s Adventures in Wonderland, Carroll was a published mathematician, usually under his real name, Charles Dodgson. However, Dodgson chose to instead publish The Game of Logic and Symbolic Logic under his pen name. Rosenhouse notes this appropriateness, as these works characterize Aristotelian logic as not only a formal study of reasoning, but also as a game for children.

In Figure 4 we see an example of Carroll’s polygonal alternative to John Venn’s diagram. With three categories we have $2^3=8$ regions representing items that are Exams (the upper half of the entire figure) or not (the lower half), Puzzles (the left half of the entire figure) or not (the right half), and Neat (within the inner square) or not (outside the inner square). As in the usual Venn diagram, overlapping regions correspond to the presence of multiple characteristics. For instance, the region in the upper half of the inner square corresponds to being both neat and exams. Rosenhouse explains that Carroll would have readers place gray markers in regions that represent items that don’t exist. Thus for the claim “all exams are not neat,” players should mark the two inner/upper regions with gray markers to represent the absence of neat exams. Likewise, from “all puzzles are neat” one should mark the two outer/left regions with gray markers, since not-neat puzzles don’t exist. Since this results in gray markers occupying the two regions corresponding to puzzles and exams (quadrant 2), we can conclude “no exams are puzzles,” as visualized on the right side of Figure 4. This “empuzzlement” (an apt term coined by Rosenhouse) of Aristotelian logic was a delight to read about, and brings to mind the joyful games and activities used in contemporary informal mathematics education, such as James Tanton’s Exploding Dots 1.

Figure 4.

Carroll diagram on exams and puzzles.

Of course, Carroll’s puzzles were not all so trivial, and Rosenhouse walks the reader through the development of not only more elaborate diagrams, but also Carroll’s symbolic calculus for modeling such conundra. While the formula $xm_0\dagger y_1m_0' \mathbin{⁋}xy_0$ may appear esoteric, Rosenhouse dedicates a chapter to explaining these expressions and (as he does throughout the text) challenges readers to solve relevant puzzles as they work along.

The other primary focus of Rosenhouse’s book is on the work of Smullyan, whose Knights and Knaves were mentioned earlier. In such story-puzzles, citizens of a certain island are all either Knights who never lie, or Knaves who always lie. As a visitor to this community, you might hear three islanders say the following.

•

A: B is a Knave.

•

B: A is a Knave.

•

C: Neither myself nor A is a Knight.

Now if I’ve done my job as the puzzle designer, you should have enough information to logically determine which persons are Knights, and which are Knaves. To do this, one might write out a truth table, as we often do for students learning to write proofs. Since $A$’s claim is $\neg B$ (“$B$ lies”), the $A$ and $\neg B$ columns should both be true (T) or both be false (F). Likewise, $B$ should match $\neg A$, and $C$ should match $\neg (A\vee C)$.

Figure 5.

Partial Knight/Knave truth table.

$A$	$B$	$C$	$\neg B$	$\neg A$	$\neg (A\vee C)$
T	F	T	T	F	F
T	F	F	T	F	F
F	T	T	F	T	F

Completing Figure 5, one may conclude that A must be the sole Knight. Of course, as with mathematics, the fun is in thinking through elegant proofs without resorting to such a brute force method. Rosenhouse shows the reader several puzzles of this genre, but I found myself pleasantly surprised when one or two chapters later, these Knights and Knaves had been transformed into the devices by which Smullyan had empuzzled Gödel’s celebrated incompleteness theorems, with “established Knights” playing the role of provable statements and “unestablished Knights” playing the role of true statements that cannot be proven.

Casting deep results such as these into a text written for a general audience is a challenge. Indeed, the third chapter ends with an apology to the reader for testing their patience with the technical details of Aristotelian Logic, and this is not the only chapter that risks leaving many readers bogged down in the weeds. Additionally, with such heavy material spanning over 300 pages, errata are sure to follow, such as one subtle mistake referring to “unestablished Knights” rather than “not (established Knights).” Fortunately, Rosenhouse does an excellent job of isolating technical arguments into sections of the book that can be tackled or skimmed by the reader as they wish, without detracting from later discussions.

The book concludes with a few miscellaneous chapters. As alluded to earlier, this includes explorations of Knights and Knaves based on nonclassical fuzzy and multivalued logics. Rosenhouse discusses metapuzzles and paradoxes, as well as the so-called “Hardest Logic Puzzle Ever.” Finally, the book concludes with an enjoyable tour of several “logic detectives” depicted in Western literature.

If you are like me, you enjoy solving puzzles at least as much as reading about them. And with ninety-one in the book, I have yet to work them all out, a task I look forward to returning to. Generally solutions are provided at the end of each chapter, although they occasionally appear in context instead when essential for the discussion at hand.

As for a recommendation, I will defer to the Knights/Knaves below.

•

A: You enjoy the narrative logic puzzles of Lewis Carroll or Richard Smullyan.

•

B: You are interested in the mathematical and logical foundations of such puzzles.

•

C: You don’t mind that discussion of other genres of logic puzzles is limited.

•

D: Either I’m a Knave, or you will enjoy this book if and only if we are all Knights.