a Graphical Design?

Graphical designs are quadrature rules for graphs $G=(V,E)$. Broadly speaking, a graphical design is a relatively small subset of vertices that captures the global behavior of functions $f:V \to \mathbb{R}$. We motivate the precise definition through numerical integration on the sphere.

The regular icosahedron (Figure 1) inscribed in the unit sphere $\mathbb{S}^2 \subset \mathbb{R}^3$ has the following amazing property: for any polynomial $p(x,y,z)$ of degree at most 5, the average of $p$ on the vertices of the icosahedron is equal to the average of $p$ over $\mathbb{S}^2$. By exploiting symmetry, these 12 points exactly average the 36-dimensional vector space of polynomials with degree at most 5. More generally, a spherical $t$-design 3 is a finite subset of points $X \subset \mathbb{S}^2$ chosen so that for any polynomial $p(x,y,z)$ of degree at most $t$,

$$\frac{1}{|X|} \sum _{(x,y,z)\in X} p(x,y,z) = \frac{1}{4\pi } \int _{\mathbb{S}^2} p(x,y,z) \ d \sigma .$$

Figure 1.

The regular icosahedron is a spherical 5-design.

The space of polynomials restricted to the sphere is spanned by the eigenfunctions of the spherical Laplacian $\Delta$, known as spherical harmonics. What is a natural analogue of spherical harmonics for a graph? We start by defining an operator analogous to $\Delta$ for a finite, undirected graph $G= (V,E)$. Let $A \in \mathbb{R}^{V\times V}$ be the adjacency matrix of $G$ defined as $A_{uv} = 1$ if $uv\in E$ and 0 otherwise, and let $D\in \mathbb{R}^{V\times V}$ be the diagonal matrix with $D_{vv} = \deg (v)$, the number of edges adjacent to $v$. Then $L = AD^{-1}$ behaves similarly to $\Delta$ in that for a function $f: V \to \mathbb{R}$,

$$\begin{align*} (Lf)(v) = \sum _{u: uv \in E} \frac{f(u)}{\deg (u)}, \end{align*}$$

averages $f$ in the neighborhood of $v$.

Figure 2.

An 11-graphical design on the truncated icosahedral graph.

Figure 3.

The contiguous United States graph. Vertices are states, and edges connect adjacent states. Each eigenvector $\varphi _i$ was affinely transformed so that $\min _j \varphi _i(j) = 0$ and $\max _j \varphi _i(j) = 1$. The interval $[0,1]$ was assigned a smooth gradient. With respect to the graph geometry, $\varphi _2$ and $\varphi _3$ are smooth, but $\varphi _{18}$ is not so smooth.

Spherical harmonics are ordered by their degree as polynomials, also called frequency. Similarly, the eigenvalues $\lambda _j$ of $L$ can be ordered as

$$1=|\lambda _1| \geq |\lambda _2| \geq \ldots \geq |\lambda _n| \geq 0.$$

Here $|\lambda _i| > |\lambda _j|$ means $\lambda _i$ is lower frequency than $\lambda _j$. This also orders the eigenspaces of $L$; if the eigenspace $\Lambda _i$ has eigenvalue $\lambda _i$, we write $\Lambda _i \leq \Lambda _j$ if $|\lambda _i| \geq |\lambda _j|$. With this ordering, low-frequency eigenvectors respect the structure of $G$ (see Figure 3). The spectrum of $L$ is a rich object of study in its own right in spectral graph theory. Throughout this paper, let $G = (V,E)$ be a graph for which $L$ has $m$ distinct eigenspaces ordered from low to high frequency as $\Lambda _1 \leq \dots \leq \Lambda _m$.

Definition 1 (17).

A subset $W \subset V$ averages an eigenspace $\Lambda$ of $L$ if for all $\varphi \in \Lambda$,

$$\begin{equation} \frac{1}{|W|} \sum _{w \in W} \varphi (w) = \frac{1}{|V|}\sum _{v \in V} \varphi (v). \tag{1}{} \end{equation}$$

To mimic the qualities of a spherical $t$-design, we seek vertex subsets that exactly average the low frequency eigenspaces of $L$.

Definition 2.

A $k$-graphical design on $G$ is $W \subset V$ that averages $\Lambda _1$, …, $\Lambda _k$.

Figure 2 shows an 11-graphical design on the trucated icosahedral graph. These 30 vertices average a 49-dimensional subspace of the 60-dimensional space of functions $\{f:V\to \mathbb{R}\}$. We call a subset that averages as many eigenspaces as possible for the graph a maximal design. Figure 4 shows a maximal design; no proper subset can average 14 or more of the 16 eigenspaces.

Graphical designs have strong connections to the combinatorics of a graph, especially in the presence of structure and symmetry. A gallery of designs can be found at: https://sites.math.washington.edu/~GraphicalDesigns/.

Figure 4.

A 13-graphical design on the J7 Flower Snark.

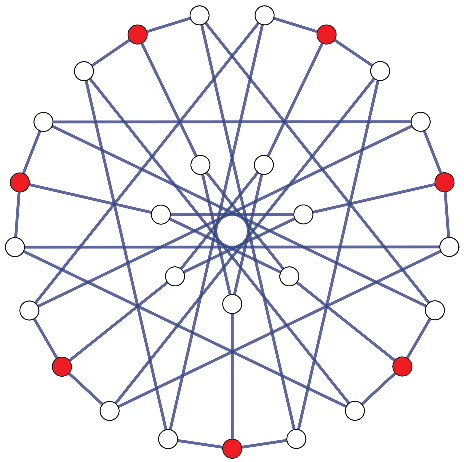
We can generalize Definition 1 by allowing weighted sums on the left of 1 and call these subsets weighted designs (Figure 5). Weighted designs are connected to oriented matroid duality and the rich literature of eigenpolytopes 2.

The neighborhood of a graphical design

Graphical designs were introduced by Steinerberger in 7. The $j$-neighborhood of a subset $W\subset V$ is the set of vertices that are at most $j$ edges away from $W$. Steinerberger shows that if $W\subset V$ is a graphical design, either the $j$-neighborhoods of $W$ grow exponentially, or $|W|$ is large. Indeed, in Figures 2, 4, and 5, the 1-neighborhood of $W$ is $V$. In Figure 6, the 1-neighborhood of $W$ is 2072 of 2277 vertices, and the 2-neighborhood of $W$ is $V$.

Figure 5.

A weighted 8-graphical design on the Szekeres Snark. Pink indicates a smaller weight – all weights are positive.

Extremal graphical designs

In 4, Golubev considered extremal designs, which are subsets $W\subset V$ that integrate all but one eigenspace of $L$, though this eigenspace may come anywhere in our frequency ordering. As an example, the Kneser graph $KG(n,k)$ has vertices corresponding to the $k$-element subsets of $\{1,\ldots , n\}$. Two vertices are adjacent if their subsets are disjoint. Golubev shows that extremal configurations from the Erdős-Ko-Rado theorem, namely a subset of vertices corresponding to all the $k$-element subsets of $[n]$ containing a fixed element, are extremal designs on $KG(n,k)$.

Graphical designs in Cayley graphs

Cayley graphs are created from an underlying group, and this additional structure can provide enough information for explicit constructions.

Denote the $d$-dimensional cube graph by $Q_d= G(\{0,1\}^d, E)$, where $uv \in E$ if $u,v \in \{0,1\}^d$ differ on exactly one coordinate. Graphical designs on this family of Cayley graphs connect to error correcting codes. We can interpret the vertices of $Q_d$ as bit strings, and subsets $W\subset V =\{0,1\}^d$ as codes. The $(7,4)$ Hamming code is the “best” $k$-graphical design on $Q_7$ in several senses; it is maximal, it is extremal, and it optimizes the ratio between $|W|$ and $\dim (\Lambda _1 ) + \ldots +\dim (\Lambda _k)$. All minimal extremal designs of cycles and cocktail party graphs, two other families of Cayley graphs, are described in 2.

Applications and connections

Graphical designs lie at an exciting intersection between contemporary applications and mathematical theory. The appearance of the graph Laplacian suggests further ties to spectral graph theory, 1 connects to coding theory, and extremal combinatorics appears in 4. Graphical designs in Cayley graphs are rooted in group representations, and probabilistic tools were used in 7.

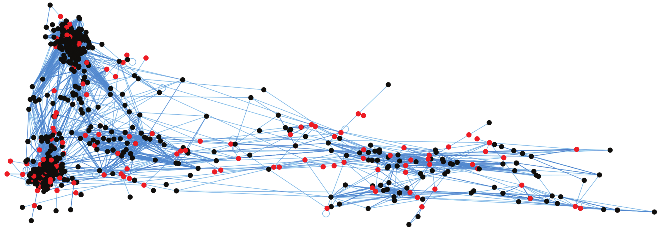
Modern data, such as social networks, ad preferences, movie recommendations, and traffic updates, is often modeled through graphs, driving a need for new data processing methods. The relatively new field of graph signal processing 5 seeks to extend classical signal processing techniques to the domain of graphs. Graphical designs provide a framework for graph sampling and numerical integration on graphs. For instance, Figure 6 shows a weighted graphical design with all positive weights on a highly nonlinear graph from real world data. In applications, it may suffice to look for approximate designs where the equality in 1 is relaxed. This can be modeled via optimization.

Figure 6.

The 228 red vertices are a weighted 229-graphical design on this network of 2277 English-language Wikipedia pages related to chameleons 6. Vertices represent pages, and edges join pages that are mutually connected by hyperlinks.