Caroline Series and Hyperbolic Geometry

1. Introduction

Caroline Series has made important contributions to hyperbolic geometry and symbolic dynamics, and her elegant and clear explanations of the connections between these two topics together with carefully chosen examples that explore the beautiful geometry underlying many spaces of Kleinian groups have influenced a generation of hyperbolic geometers and dynamicists.

Caroline obtained her BA at the University of Oxford in 1972 and her doctorate at Harvard University in 1976 under the supervision of George Mackey. She spent the first couple of years of her career at Berkeley and Cambridge before settling in Warwick in $1978$, where she stayed until her retirement in $2014$. Her stint at Berkeley led to an important but short-lived collaboration with Rufus Bowen which ended abruptly when Bowen passed away unexpectedly in July 1978. Her work on the connections between symbolic dynamics and hyperbolic geometry done during the early period of her career led to an invitation to speak at the ICM at Berkeley in $1986$. She has received numerous awards and honors for her work including the Senior Anne Bennett Prize (LMS, 2014), Junior Whitehead Prize (LMS, 1987), Fellow of the Royal Society (2016), and the David Crighton Medal (IMA-LMS, 2021). She has honorary degrees from Duke and St Andrews Universities and is a Fellow of the AMS. She served as president of the LMS (London Mathematical Society) from 2017 to 2019.

The 1990s and 2000s saw intense activity in the fields of hyperbolic geometry, hyperbolic $3$-manifolds, and Kleinian groups following the revolutionary ideas and conjectures of William Thurston. Many important conjectures like Thurston’s geometrization conjecture, Marden’s tameness conjecture, the virtual Haken conjecture, the ending lamination conjecture, and the Ahlfors measure conjecture were solved during this period. During her tenure at Warwick, working alongside David Epstein, Caroline played a pivotal role in helping to make the Mathematics Institute there a leading international center for hyperbolic geometry, organizing many large conferences and programs attended by leading researchers in the field. She also played host and mentor to a large number of young international visitors, particularly researchers from Japan. We give below a description of some of her considerable contributions to the field.

2. Symbolic Dynamics and Fuchsian Groups

Caroline wrote her thesis on Mackey’s theory of virtual groups, which involves the ergodic theory of groups acting measurably on measure spaces; in particular two groups $G, G'$ acting on measure spaces $X, X'$ and preserving measure classes $\mu , \mu '$ are said to be orbit equivalent if there is a measure class preserving map $T$ from $X$ to $X'$ which sends the orbits of $G$ to the orbits of $G'$. Note that $G, G'$ are not necessarily isomorphic, nor does $T$ necessarily preserve any order in individual orbits. By a remarkable result of H. Dye, all finite measure preserving actions of $\mathbb{Z}$ are orbit equivalent; such actions are called hyperfinite. Caroline’s first contributions involved various results in this area; see for example Ser78.

Starting in the late 1970s, Caroline wrote a number of important papers elucidating the connections between hyperbolic geometry and symbolic dynamics. We start with a simple but very illuminating result concerning continued fractions and cutting sequences of geodesics.

Figure 2.

The cutting sequence of $x=9/5=[1;1,4]$ and $y=23/5=[4;1,1,2]$ across the Farey tessellation.

2.1. Continued fractions and cutting sequences

Recall that the upper half plane

$$\mathbb{H}^2=\{z \in \mathbb{C}\nobreakspace |\nobreakspace \Im z>0\}$$

and the unit disk

$$\mathbb{D}=\{z \in \mathbb{C}\nobreakspace |\nobreakspace |z|<1\}$$

both serve as models for the hyperbolic plane with ideal boundary $\partial \mathbb{H}^2=\mathbb{R}\cup \{\infty \}$ and $\partial \mathbb{D}= S^1$ respectively. In an elegant paper Ser85b, Caroline explained the beautiful relationship between the continued fraction of $x\in \mathbb{R}$ and the manner in which the hyperbolic geodesic joining some point on the positive imaginary axis to $x$ cuts across the Farey triangulation of $\mathbb{H}^2$. That there seemed to be a close connection between continued fractions and cutting sequences of geodesics across the classical fundamental domain of the modular group had been known for some time, but details remained elusive. Caroline was the first to give a precise relation using the left/right cutting sequences explained next.

The Farey triangulation $\mathcal{F}$ of $\mathbb{H}^2$ is a tessellation by triangles each of whose vertices lie in $\mathbb{Q}\cup \{\infty \}$. Its edges are the hyperbolic geodesics joining Farey neighbors, where two fractions $\frac{p}{q}, \frac{m}{n} \in \mathbb{Q}\cup \infty$ in reduced form are called Farey neighbors if $|pn-qm|=1$, with the convention that $\frac{1}{0} = \infty$. (Recall that a geodesic in $\mathbb{H}^2$ is a semicircle with center on $\mathbb{R}$ or a vertical line.) The tessellation $\mathcal{F}$ can be built up recursively using “Farey addition” as follows; for simplicity we restrict to the right half plane. Start from an initial triangle with vertices at $\infty =\frac{1}{0}$, $\frac{0}{1}$ and $\frac{1}{1}$ and note that each pair of vertices are neighbors. Two Farey neighbors $\frac{p}{q}$ and $\frac{m}{n}$ spawn a new vertex $\frac{p+m}{q+n}$ which is a neighbor of both. Thus, for example, neighbors $\frac{1}{0}, \frac{1}{1}$ spawn $\frac{2}{1}$, while $\frac{0}{1}, \frac{1}{1}$ spawn $\frac{1}{2}$. Joining each pair with a hyperbolic geodesic defines new triangles with vertices $\{\frac{1}{0}, \frac{1}{1}, \frac{2}{1}\}$ and $\{\frac{0}{1}, \frac{1}{1},\frac{1}{2} \}$. Repeating this procedure generates $\mathcal{F}$.

Now let $x>0$ and consider the oriented geodesic $\gamma _x$ from a point on the positive imaginary axis to $x>0$. Its left/right cutting sequence across $\mathcal{F}$ is defined as follows: if $\gamma _x$ cuts a triangle of $\mathcal{F}$ with single vertex on the left it is recorded as a left cut $L$, while if the single vertex is on the right, it is a right cut $R$; see Figure 2. The cutting sequence for $\gamma _x$ is then $L^{n_0}R^{n_1}L^{n_2}\ldots$, with the convention that the initial term $L^0$ is omitted if $0<x<1$.

Now suppose $x>0$ is expressed by the continued fraction

$$\begin{equation*} x=[a_0;a_1,a_2,\ldots ]\coloneq a_0+\cfrac {1}{a_1+\cfrac {1}{a_2+\cdots }} \end{equation*}$$

where $a_0 \in \mathbb{N}\cup \{0\}$, $a_i \in \mathbb{N}$ for $i \ge 1$. Then

Theorem 2.1.

(Series Ser85b 1985) For $x>0$, its continued fraction is $[a_0;a_1,a_2,\ldots ]$ if and only if the geodesic $\gamma _x$ ending at $x$ has left/right cutting sequence $L^{a_0}R^{a_1}L^{a_2}\ldots$.

Notice that if $x \in \mathbb{Q}$ then $\gamma _x$ ends at a vertex of the tessellation so that the label of the final cut is ambiguous, corresponding exactly to the ambiguity in the final terms $[\ldots a_n,1]$ or $[\ldots ,a_{n}+1]$ of finite continued fractions. Left/right cutting sequences are now widely used.

2.2. Special tessellations and symbolic dynamics

This theme of using special tessellations of $\mathbb{H}^2$ or $\mathbb{D}$ arising from Fuchsian groups with special fundamental domains, and the associated cutting sequences, to describe the dynamical behavior of the geodesic flow occurs in several of Caroline’s other works. In particular, it features in an earlier well-known paper BS79 with Bowen which explained the connection between Fuchsian groups and symbolic dynamics. Here it is convenient to use the model $\mathbb{D}$ with ideal boundary $\partial \mathbb{D}\cong S^1$ and isometry group $\operatorname {Isom}^+(\mathbb{D})\cong \mathrm{PSL}(2,{\mathbb{R}})$.

Recall that if $\Gamma$ is a finitely generated Fuchsian group, then $\Gamma < \operatorname {Isom}^+(\mathbb{D})$ is discrete and $\mathbb{D}/\Gamma$ is a hyperbolic surface, possibly with cusps, boundary components, and cone points.

A piecewise differentiable map $f: S^1 \to S^1$ is called Markov if there is a finite partition of $S^1$ into intervals $I_j$ such that $f(I_j)$ is a union of intervals $I_k$. This means that the associated symbolic dynamics is of finite type; that is, an infinite sequence $I_{i_1}$, $I_{i_2}$, $I_{i_3}$, … of labels records the intervals through which an orbit of $f$ passes if and only if each pair of adjacent symbols in the sequence is permissible. Furthermore, the map $f$ is orbit equivalent to the action of the Fuchsian group $\Gamma$ on $S^1$ if, except for a finite number of pairs of points, $x,y \in S^1$, $x=gy$ with $g \in \Gamma$ if and only if there exists $n, m \ge 0$ such that $f^m(x)=f^n(y)$.

Theorem 2.2.

(Bowen, Series BS79) For any finitely generated Fuchsian group $\Gamma$, there exists a Markov map of $S^1$ which is orbit equivalent to the action of $\Gamma$ on its limit set $\Lambda \subset S^1$. This map admits a unique finite invariant measure, which, in the case of a group for which $\Lambda = S^1$, is equivalent to the Lebesgue measure.

For any surface $\Sigma$ of fixed topological type, the proof involves the clever idea of first considering a particular Fuchsian group $\Gamma$ whose quotient surface $\mathbb{D}/\Gamma$ is homeomorphic to $\Sigma$, together with a special type of fundamental domain $D$ with corresponding tessellation of $\mathbb{D}$ (described below). This is used to construct the partition of $S^1$ and the Markov map of the theorem. Then using the theory of quasiconformal deformations, the result can be extended to a general Fuchsian group whose quotient is homeomorphic to $\Sigma$.

A fundamental domain $D$ in $\mathbb{D}$ is special if it is a finite-sided convex polygon whose sides, when extended, are contained in the tessellation of $\mathbb{D}$ arising from the translates of $D$ in $\mathbb{D}$. The sides should be matched in pairs by isometries which form a generating set for $\Gamma$. From this one constructs a partition of $S^1 =\partial \mathbb{D}$ with the requisite Markov property, and such that moreover each interval in the Markov partition is associated to a specific generator of $\Gamma$. ⁠¹

¹

In BS79 it was required that the sides $\partial D$ of the fundamental domain were part of the isometric circles of the corresponding side pairings of $D$, but in fact this condition is not necessary.

✖

Continuing along the same lines, in Ser81, Caroline explicitly constructs a symbolic dynamics for the geodesic flow on any hyperbolic surface by associating to each geodesic a doubly infinite sequence in the two-sided extension of the above Markov shift. Roughly speaking, this is done by mapping the two endpoints of a lifted geodesic $\gamma$ to the semi-infinite sequences associated to it by the Bowen–Series map constructed above. By making precise the connection between this coding and the cutting sequence obtained by reading off the labels of sides of $D$ traversed by $\gamma$ in its passage across $\mathbb{D}$, she elucidated the connection between the Artin and Koebe–Morse methods for obtaining symbolic representations of geodesic flows on surfaces of constant negative curvature; see also Ser86. This circle of ideas is now a standard starting point for many results on orbit counting and symbolic dynamics. Later, she made many applications of this coding to Fuchsian groups, for example to the word problem BS87, to random walks Ser83, to group cohomology BS84, and to simple curves on surfaces, of which more below.

Figure 3.

Caroline with colleagues David Fowler (left) and David (Dai) Evans in the maths common room at Warwick, 1980.

3. Curves on Surfaces

In the $1980$s, together with Joan Birman, Caroline wrote a series of papers studying curves on hyperbolic surfaces, in particular their self-intersection numbers. These used many of the ideas she had used in her earlier work on cutting sequences of geodesics and the associated symbolic coding. The most influential of these was a paper containing a remarkable theorem about the sparsity of the set of points lying on complete geodesics with bounded self-intersection on a hyperbolic surface of finite type, that is, of finite genus with finitely many cusps or boundary components.

3.1. Geodesics with bounded self-intersections

Let $\Sigma$ be a closed hyperbolic surface of finite type and let $G_k$ be the set of all complete geodesics on $\Sigma$ which have at most $k$ self-intersections. In particular, $G_0$ is the set of complete simple geodesics on $\Sigma$.

Theorem 3.1.

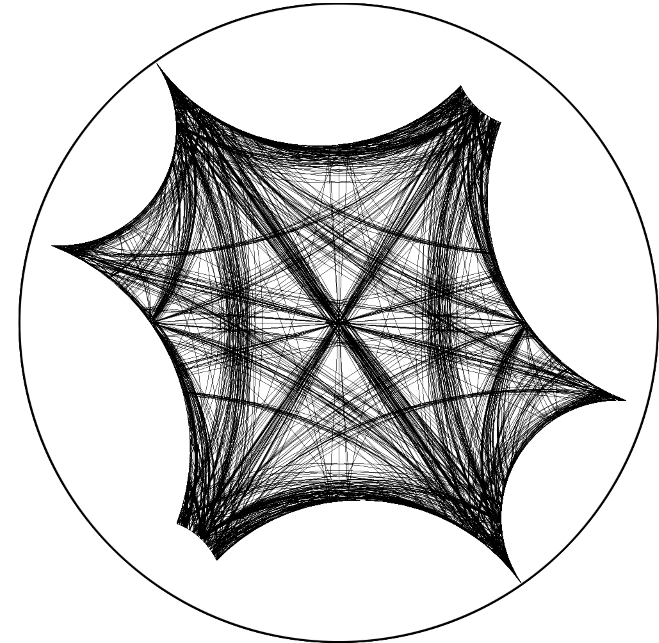
(Birman, Series, BS85 1985) Let $k \ge 0$. The set $S_k$ of points on $\Sigma$ lying on any geodesic $\gamma \in G_k$ is a set of Hausdorff dimension $1$ and is nowhere dense.

This result contrasts with the case of a Euclidean torus $E$ where every point on $E$ is contained in some simple geodesic. It also contrasts with the case of a generic geodesic on $\Sigma$ which is typically dense on $\Sigma$. The set $S_0$ is now commonly referred to as the Birman–Series set.

The main idea behind the proof is very simple and elegant. We give a brief sketch for the case of simple geodesics on a closed hyperbolic surface $\Sigma$.

Figure 4.

The first $300$ or so simple curves ordered by length on a genus two surface $\Sigma$. Graphics by Peter Buser and Hugo Parlier from their paper “Quantifying the sparseness of simple geodesics on hyperbolic surfaces.”

Choose a finite-sided convex polygonal fundamental domain $D$ for $\Sigma$ with $m$ sides $s_1, \ldots , s_m$ labelled on the inside. The images of $D$ under $G = \pi _1(\Sigma )$ define a tessellation $\mathcal{T}$ of $\mathbb{H}^2$ and the $G$ action carries the labelling to each copy of $D$ in $\mathcal{T}$. Suppose $\gamma$ is a simple geodesic (closed or otherwise) on $\Sigma$. Since $D$ glues up to reconstitute $\Sigma$, the lifts of $\gamma$ to $\mathbb{H}^2$ appear as a collection of disjoint strands $\sigma _i$ across $D$. Starting with the strand $\sigma _0$ and working backward and forward, we can trace the sequence of sides $\ldots a_{-1}a_0a_1\ldots , a_i \in \{ s_i\}$ in which $\gamma$ cuts $D$, numbered so that $\sigma _0$ is the strand between labels $a_0$ and $a_1$. This is called the cutting sequence of $\gamma$.

Now suppose that $\gamma$ and $\gamma '$ are two such geodesics whose cutting sequences $\ldots a_{-1}a_0a_1\ldots$ and $\ldots a'_{-1}a'_0a'_1\ldots$ are such that $a_i=a'_i$ for $-N\le i \le N$. Lifting $\gamma$ and $\gamma '$ to $\mathbb{H}^2$ in such a way that $\sigma _0, \sigma '_0$ are the strands between labels $a_0, a_1$ and $a'_0, a'_1$, we see that the initial segments $\sigma _{-N}, \sigma '_{-N}$ of the lifts $\tilde{\gamma }$ and $\tilde{\gamma }'$ begin at points $x, x'$ on the same side of the same copy of $D$, so that $x, x'$ are a bounded distance apart, and likewise for the final points of the segments $\sigma _{N}, \sigma '_{N}$. It follows from the properties of hyperbolic geodesics that the segments $\sigma _0, \sigma _0'$ between the cuts labelled $a_0, a_1$ are exponentially close, that is, they lie in some strip connecting two sides of $D$ of width less than $e^{-cN}$ for some constant $c>0$.

Requiring that a geodesic $\gamma$ is simple is extremely restrictive because its segments across $D$ must all be disjoint. These segments can be isotoped so that each crossing of a side of $D$ is at the midpoint of the side, resulting in a graph $\Gamma$ whose vertices are the midpoints of sides of $D$ and whose edges are arcs between these vertices. Moreover all its edges are disjoint. Clearly there are only finitely many such graphs. Now given the number $n_{ij}$ of arcs between the sides labelled $s_i$ and $s_j$, one can reconstruct up to isotopy the segment of $\tilde{\gamma }$ between the initial and final points $x,y$. If $\gamma$ and $\gamma '$ share the same $N$th forward and backward cutting sequences, then $n_{ij } = n'_{ij }$ for all $i,j$ and moreover $\Sigma _{i,j} n_{ij }= 2N$. It follows that there are only $P(N)$ possibilities for the cutting sequences, where $P$ is a polynomial of degree equal to the number of edges of $\Gamma$. Hence the projections of the segments $s_0, s_0'$ onto $D$ lie in a collection of strips of width bounded by $e^{-cN}$ for some $c>0$, and the number of such strips is bounded by $P(N)$. Letting $N \rightarrow \infty$ gives the result.

Notice that this also gives a polynomial upper bound for the number of simple curves of length bounded by $N$; this type of bound was vastly improved by Mirzakhani; see the next section.

The proof can be adapted easily to the case of geodesics with bounded intersection, and for surfaces with cusps and/or geodesic boundary. The Birman-Series set $S_0$ contains a wealth of information and has been intensively studied. An illustration of a subset of $S_0$ on a perturbation of the Bolza surface (the genus two surface with maximal symmetry group) is given in Figure 4.

3.2. Identities and other applications

The above result has many consequences, and also raises many questions about geodesics of bounded intersection on $\Sigma$. It has led to an active field of research and some surprising applications. In his Warwick PhD thesis, Greg McShane studied the nature of the Birman–Series set for a hyperbolic once-punctured torus, and in particular its intersection with the horocycle of length one about the cusp. This is a nowhere dense subset of zero measure on the horocycle, and by studying the complementary gaps, he obtained the following remarkable identity:

Theorem 3.2 (McShane, 1991).

Let $T$ be a complete hyperbolic once-punctured torus. Then

$$\sum _{\gamma }\frac{1}{1+e^{l(\gamma )}}=\frac{1}{2}$$

where the sum is over the set of simple closed geodesics on $T$ and $l(\gamma )$ denotes the length of $\gamma$.

This was subsequently generalized first by McShane himself to general surfaces with cusps McS98 and then by Maryam Mirzakhani Mir07 to surfaces with geodesic boundary, where, in a tour de force, she used her formulae to determine the volumes of the moduli spaces of surfaces with geodesic boundary. There is now a large body of work on various other generalizations and applications by Bowditch, Akiyoshi–Miyachi–Sakuma, Tan–Wong–Zhang, Labourie–McShane, and several others which trace their inspiration to the original Birman–Series result.

In another direction, as noted above, the Birman–Series result raises the question of the growth rate of geodesics in $G_k$ with length less than $L$ as $L \rightarrow \infty$. This has also led to a large body of work, notably by Rivin, Mirzakhani ($k=0$), Erlandsson–Souto ($k>0$), Sapir, and Erlandsson–Parlier–Souto.

4. Pleating Rays

In the 1990s, Caroline shifted her attention to Kleinian groups⁠² and hyperbolic three manifolds. Together with Linda Keen, she invented the theory of pleating rays. These rays (or their higher-dimensional analogues pleating varieties) foliate spaces of various parametrized families of Kleinian groups. Initially inspired by the computer graphics of Mumford and Wright which showed that the limit sets of many two generator groups consist of chains of overlapping or tangent circles such as are clearly visible in Figure 6, the theory was initially worked out with Keen in the case of two special one complex dimensional families, the Maskit and Riley slices of Schottky space, described in more detail below.

²

A Kleinian group is a discrete group of orientation-preserving isometries of hyperbolic $3$-space $\mathbb{H}^3$, identified with $\mathrm{PSL}(2,{\mathbb{C}})$.

✖

4.1. Background

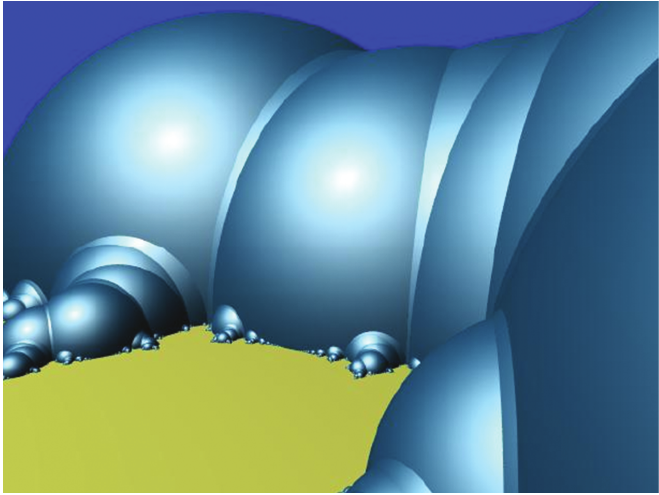
As Keen and Series discovered, the key to understanding these Mumford–Wright graphics is to pass to the hyperbolic convex hull $\mathcal{C}$ of the limit set $\Lambda$ of a Kleinian group $G$ in hyperbolic $3$-space. Thurston described the boundary $\partial \mathcal{C}$ as a pleated surface: this is a surface made up of pieces of hyperbolic planes, meeting along hyperbolic lines called bending lines; see Figure 5. This surface itself carries an intrinsic hyperbolic structure so that $\partial \mathcal{C}/G$ is a collection of hyperbolic surfaces. Also recall that $G$ acts discontinuously on $\Omega$, the complement of the limit set $\Lambda$ in $\mathbb{C}\cup \infty$ and that the quotient $\Omega /G$ is a collection of Riemann surfaces. It can be shown that the surfaces $\partial \mathcal{C}/G$ are homeomorphic to the Riemann surfaces $\Omega /G$, although with different hyperbolic structures.

Using this circle of ideas, Keen and Series were able to relate circle patterns in $\Lambda$ to the shape of $\partial \mathcal{C}/G$. In the upper half space model of hyperbolic space $\mathbb{H}^3$, a plane is a vertical half plane or a hemisphere with center on the boundary $\partial \mathbb{H}^3$, identified in this model with $\mathbb{C} \cup \{\infty \}$. Likewise a hyperbolic geodesic or line is a vertical line or semicircle with center on $\mathbb{C} \cup \{\infty \}$. Thus a circle or arc of a circle in $\Lambda$ gives rise to a plane or part plane in $\partial \mathcal{C}$, likewise two circles which overlap give rise to intersecting planes which meet along a bending line in $\partial \mathcal{C}$. The bending lines project to disjoint geodesics on $\partial \mathcal{C}/G$ and thus are either simple closed curves or, in the case of non-closed curves, what Thurston called a (measured) geodesic lamination. Such laminations can be organized as a space of projective measured laminations, denoted $\mathcal{PML}$; for present purposes it suffices to note that $\mathcal{PML}$ contains simple closed curves or multi-curves as a dense subset. Such laminations are called rational for reasons which will be clearer in the next section.

Figure 5.

The boundary of the hyperbolic convex hull of a Kleinian group limit set is a pleated surface made up of pieces of hyperbolic planes meeting along hyperbolic geodesics called bending lines.

A pleating ray as introduced by Keen and Series is by definition the locus in some parameter space of Kleinian groups on which the bending lamination is a fixed element in $\mathcal{PML}$. It is called rational if the corresponding lamination is rational, that is, comes from bending lines which project to simple closed curve or multi-curves on $\partial \mathcal{C}/G$. In the case of “rational rays” the limit set of the group is formed by chains of overlapping circles such as are apparent, for example, in Figure 6. Movement along the ray corresponds to keeping the same combinatorial pattern while varying the radii and angles of overlap between the circles. A key point for both theory and computations is that on a rational ray, the traces of the corresponding group element or elements are real valued.

Using some of the powerful ideas of Thurston theory, Keen and Series were able to show the rational rays have many remarkable properties. In spaces involving one complex parameter such as the Maskit and Riley slices described below, they were able to compute the rational rays explicitly showing that they fill out the entire space of discrete free groups in the given family densely. This gave in particular an algorithmic way in which to locate the boundary between discrete and non-discrete groups.

This should all become clearer when we look at two particular examples explained in the following two sections.

4.2. The Maskit slice

Figure 6.

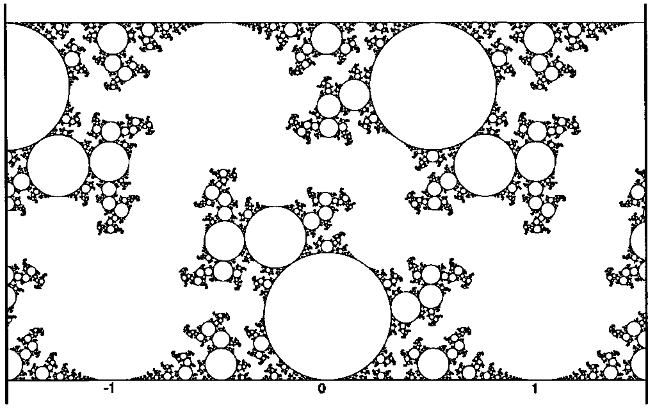
Limit set of a group on the $3/10$ ray in the Maskit slice, $\mu = 0.5 + 1.6583124i$. The disks bounded by full circles in $\Lambda _{\mu }$ all project to the triply punctured sphere boundary while the overlapping circles give rise to part hyperbolic planes. The lines along which they intersect project to the $3/10$ curve on $T_{1,1}$.

Figure 7.

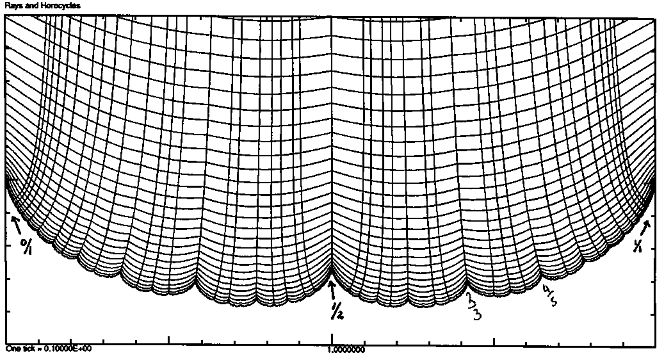
The Maskit slice. The pleating rays are the approximately vertical lines. The approximately horizontal lines represent laminations with the same length, appropriately normalized.

Let

$$G_{\mu } =\Big \langle X\coloneq \begin{pmatrix} 1 & 2 \\ 0 & 1 \end{pmatrix}, Y_{\mu }\coloneq -i\begin{pmatrix} \mu & 1 \\ 1 & 0 \end{pmatrix} \Big \rangle , \quad \mu \in \mathbb{C}.$$

The Maskit slice is the set

$$\mathcal{M}= \{\, \mu \in \mathbb{C}\mid \text{$G_{\mu }$ is discrete and free}\, \}.$$

This set has two components which are symmetric under reflection across the real axis, both of which by results of Bers can be identified with the Teichmüller space $\mathcal{T} (T_{1,1})$ of the punctured torus $T_{1,1}$. We consider the upper component $\mathcal{M}^+$; see Figure 7.

For $\mu \in \mathcal{M}^+$, let $\Omega _{\mu }$ be the complement in ${\mathbb{C}}\cup \{\infty \}$ of the limit set $\Lambda _{\mu }$ of $G_{\mu }$. As the reader can discern from Figure 6 with a bit of effort, $\Omega _{\mu }$ consists of a simply connected component $\Omega _0$ which is invariant under the $G$ action, together with a collection of round disks each of which is fixed by a subgroup of $G_{\mu }$ and which together form a single $G$-orbit under the action. The component $\Omega _0/ G_{\mu }$ of $\Omega _{\mu }/G_{\mu }$ is a once-punctured torus $T_{1,1}$, while all the other disk components all project to a single triply punctured sphere. Since a hyperbolic triply punctured sphere is rigid, its geometry is fixed independent of $\mu$.

Now the component $\Omega _0$ faces a component $B_0$ of the convex hull boundary $\mathcal{C} (\Lambda _{\mu }) \subset \mathbb{H}^3$. As discussed in the previous section, $B_0/G_{\mu }$ is homeomorphic to $\Omega _{0}/G_{\mu }$ hence is itself a hyperbolic once-punctured torus with the hyperbolic structure induced from the ambient space $\mathbb{H}^3$. Thus the possible bending lines on the pleated surface $B_0/G_{\mu }$ are the possible geodesic laminations on $T_{1,1}$. With respect to a particular generating set, a simple closed curve on $T$ winds around $p$ times in one direction and $q$ in the other, so can be indexed by a rational number $p/q$. Thus the set of simple closed curves is identified with the rational numbers $\mathbb{Q}\cup \infty$. Thurston’s theory shows that the space of projective measured laminations $\mathcal{PML}$ on $T_{1,1}$ can be identified with the closure $\overline{\mathbb{Q}\cup \infty }$, that is, the extended real line $\mathbb{R}\cup \infty$.

Following the discussion in the previous section, the $\lambda$ pleating ray ${\mathcal{P}}_\lambda$ is the set of $\mu \in \mathbb{C}$ for which $B_0$ is bent along the lamination $\lambda$. When $\lambda$ is a rational number $p/q$, the lamination is a simple closed geodesic which after suitable normalisation can be represented by a special word $W_{p/q}$ in $X$ and $Y_{\mu }$. In particular, $\infty =1/0$ corresponds to $X=W_{1/0}$ and $0/1$ corresponds to $Y_{\mu }=W_{0/1}$. On the $p/q$ pleating ray ${\mathcal{P}}_{p/q}$ the trace of $W_{p/q}$ is necessarily real valued, but the converse is not true. (The real locus of $\operatorname {tr}(W_{p/q})$ has other branches that correspond to groups where the geodesic represented by $W_{p/q}$ lies in the interior of the convex core.)

In KS93, Keen and Series explicitly describe the rational pleating rays for $\mathcal{M}$ for this setting. Each rational ray is a connected component of the set of $\mu$ for which $\operatorname {tr}(W_{p/q}) \in [2, \infty )$ which, remarkably, contains no singularities. Moreover by analyzing the leading terms of $\operatorname {tr}(W_{p/q})$ as a polynomial in $\mu$, combined with some new results on the behavior of $\mathcal{C}$ as $\mu$ varies, they show that for real $\lambda$ the pleating ray ${\mathcal{P}}_\lambda$ is asymptotic to the line $\operatorname {Re}(\mu )=2\lambda$.

The rational pleating rays are clearly pairwise disjoint. They show further that they are dense in $\mathcal{M}$ and are interpolated by ‘irrational rays’ corresponding to non-closed bending laminations which share similar properties to the rational ones. Each rational ray ends in a unique point on $\partial \mathcal{M}$; these are the cusp groups described by Bers and Maskit. Minsky’s famous ending lamination theorem for $T$ can be viewed as the statement that the irrational rays also have a unique ending point, from which it follows that $\partial \mathcal{M}$ is a Jordan curve.

4.3. The Riley slice

Let

$$\begin{equation*} H_{\rho }= \Big \langle A\coloneq \begin{pmatrix} 1 & 1\\ 0 & 1 \end{pmatrix}, B_{\rho }\coloneq \begin{pmatrix} 1 & 0\\ \rho & 1 \end{pmatrix} \Big \rangle , \quad \rho \in \mathbb{C}. \end{equation*}$$

The Riley slice is the set

$$\mathcal{R}= \{\, \rho \in \mathbb{C}\mid \text{$H_{\rho }$ is discrete and free}\, \}.$$

This slice was studied by Keen and Series in KS94. For $\rho \in \mathcal{R}$, the complement $\Omega _{\rho }$ of the limit set $\Lambda _{\rho }$ of $H_{\rho }$ has just one connected component which is however no longer simply connected. The quotient $\Omega _{\rho }/ H_{\rho }$ is a four-times-punctured sphere $S_{0,4}$. As in the previous section, this means that the convex hull boundary $\partial \mathcal{C}(\Lambda _{\rho })/H_{\rho }$ is a pleated surface homeomorphic to $S_{0,4}$. However in this case, since $\Omega _{\rho }$ is no longer simply connected, there is a simple closed loop on $\Omega _{\rho }/ H_{\rho }$ which bounds a disk which is homotopically trivial in the hyperbolic $3$-manifold $\mathbb{H}^3/ H_{\rho }$. Such a loop cannot be realized as a bending line of $\partial \mathcal{C}(\Lambda _{\rho })/H_{\rho }$.

By realizing $S_{0,4}$ as a quotient of the plane $\mathbb{R}^2$ punctured at lattice points $\mathbb{Z}^2$, it is not hard to see that simple curves on $S_{0,4}$ are in bijective correspondence to lines of rational slope on the plane. Taking into account the homotopically trivial missing loop which we label $1/0 = \infty$, one sees that the possible bending lines are indexed by $p/q\in \mathbb{Q}/2\mathbb{Z}$, and moreover each possible bending line curve corresponds to a specific element $V_{p/q} \in H_{\rho }$. The pleating rays ${\mathcal{P}}_{p/q}$ turn out to have two symmetrical connected components each contained in the set of $\rho$ for which $\operatorname {tr}(V_{p/q})\in (-\infty ,-2]$.⁠³ Moreover, again by analyzing the top terms of $\operatorname {tr}(V_{p/q})$, Keen and Series show that for real $\lambda$ the components of the pleating ray ${\mathcal{P}}_\lambda$ are asymptotic to the lines $te^{\pm i\pi (1-\lambda )}$ for $t>0$.

³

The original paper contained an error pointed out and corrected by Y. Komori.

✖

A similar analysis for a family of groups corresponding to a hyperbolic $3$-manifold which is a handlebody with a certain $3$-fold symmetry was carried out more recently by Series, Yamashita and the second author STY17. The corresponding pleating rays are illustrated on the cover of the December 2016 AMS Notices.

Figure 8.

The Riley slice with extended pleating rays.

The family of groups $H_{\rho }$ had been investigated by Robert Riley in the 1970s. He showed that each two-bridge knot or link complement corresponds to a point in the complement of the Riley slice, thus for example, the figure eight knot complement corresponds to $\rho =e^{i\pi /3}$. With the aid of elaborate computer computations, he also identified families of discrete groups, which he called Heckoid groups, in the complement of $\mathcal{R}$. These groups generalize the Hecke groups where $\operatorname {tr}(V_{0/1})=\operatorname {tr}(AB_{\rho })=-2\cos (2\pi /m)$ or $\operatorname {tr}(V_{1/1})=\operatorname {tr}(AB_\rho ^{-1})=-2\cos (2\pi /m)$.

Following a suggestion of Sakuma, and as explained by Caroline in her 2019 Presidential Lecture, it is conjectured that the pleating rays may be analytically continued along arcs where $\operatorname {tr}(V_{p/q})\in (-2,2]$. These extensions are the black arcs outside the colored region in Figure 8. The groups along these arcs are holonomies of hyperbolic cone manifolds. The points marked by black dots correspond to the Heckoid groups for which $\operatorname {tr}(V_{p/q})=-2\cos (2\pi /m)$ for $m$ an integer at least $3$, while the rays end in the knot and link complement groups occurring when $V_{p/q}$ is the identity for which $\operatorname {tr}(V_{p/q})=2$.

As a consequence of unpublished results of Ian Agol, recently completed by Sakuma and several collaborators including the first author, the Heckoid groups and knot or link complement groups are the only discrete $H_{\rho }$ in the complement of ${\mathcal{R}}$. It follows from the above that all such groups should be located on the extended pleating rays. The pleating rays for ${p/q}=\pm 1/m$ or $\pm (m-1)/m$ may be extended to points on the real axis corresponding to Hecke groups (or the origin when $m=1$ or $2$), and the remaining rays may be extended as far as points away from the real axis corresponding to knot or link complement groups.

4.4. Pleating varieties

Subsequent to these results on the Maskit slice and the Riley slice, Caroline went on to generalize pleating rays to families of Kleinian groups depending on more parameters, thus relating to higher genus surfaces.

In one direction, Caroline considered Maskit embeddings for higher complexity surfaces. She proved general results on the top terms of the trace polynomials, first for the case of twice-punctured torus, jointly with Keen and the first author KPS99, and then for all surfaces, in joint work with her student Sara Maloni MS10. Caroline then gave formulae for the asymptotic directions of pleating varieties in the case of the twice-punctured torus, the general case being worked out by Maloni in her thesis.

In another direction, one can consider pleating varieties for families of quasifuchsian groups $G$, that is, groups for which the limit set is a Jordan curve. Thus, $\Omega$ is separated into two simply connected invariant components and $\Omega /G$ consists of two Riemann surfaces $\Sigma ^{\pm }$ each of which is homeomorphic to the same surface $\Sigma$. The corresponding parameter space is $\mathcal{T}(\Sigma ) \times \mathcal{T}(\Sigma )$, where $\mathcal{T}(\Sigma )$ is the Teichmüller space of $\Sigma$.

In this case one has to consider two geodesic laminations, $\mu$ and $\nu$, one on $\Sigma ^+$ and one on $\Sigma ^-$, and to analyze the set of those groups for which $\mu$ and $\nu$ can be the bending lines on the two components of $\partial \mathcal{C}/G$. Of particular interest is the set points where this locus meets the Fuchsian locus $\mathcal{F}$, that is, the set of groups for which the limit set is a round circle. Note that $\mathcal{F}$ can be identified with the Teichmüller space $\mathcal{T}(\Sigma )$.

Keen and Series made an initial analysis of this situation in the case of once-punctured tori and showed that all possible pairs of distinct projective laminations can occur. In PS95, she and the first author looked in detail at the case in which the bending laminations are a pair of closed curves which intersect exactly once, deriving exact formulae for the relationship between the bending angle between planes in $\partial \mathcal{C}/G$ and the geodesic length of the bending curve. These formulae were used to show that, if the two curves represent generators $A, B$ of $G$, then the corresponding pleating variety meets $\mathcal{T}(T_{1,1})$ exactly in the set of rectangular tori.

The case of twice-punctured tori was studied in various papers with Raquel Díaz, Linda Keen, and the first author. Caroline then showed in Ser05 that for any surface, the pleating variety associated to the pair of laminations $(\mu , \nu )$ meets the Fuchsian locus $\mathcal{F}$ exactly on Kerckhoff’s line of mimima for $(\mu , \nu )$ in $\mathcal{T}(\Sigma )$. This line is defined as follows: for a given $t \in (0,1)$ there is a unique point in $\mathcal{T}(\Sigma )$ at which the length of $t\mu +(1-t)\nu$ is minimized. The line of minima is the collection of all such points for $t \in (0,1)$. In particular, the set of rectangular tori in $\mathcal{T}(T_{1,1})$ is exactly the line of minima for the generating curves $A, B$ above.

In an important paper with Young Choi CS06, she went on to extend the one-dimensional result on non-singularity of pleating varieties by proving that for general Kleinian groups the complex lengths of the bending lines are local holomorphic parameters for the ambient parameter space.

Caroline has a number of other more general results on hyperbolic $3$-manifolds and Teichmüller theory, for example her variant on Wolpert’s well-known derivative formula, work with Choi and Kasra Rafi on the relationship between lines of minima and Teichmüller geodesics, and with Mahan Mj on the behavior of individual limits under geometric and algebraic convergence of groups.

Figure 9.

Caroline with Yair Minsky and Makoto Sakuma at her Spaces of Kleinian Groups programme at the Isaac Newton Institute, 2003.

5. Exposition and Service to Community

An important contribution of Caroline’s to the field has been her expository work which has brought the fascination of the subject to many young mathematicians and the broader public. Her paper Ser85a on the geometry of the Markoff numbers was a very attractive and elegant exposition of the intimate connections between number theory, Diophantine approximation, hyperbolic geometry, and the modular hyperbolic punctured torus which has been read by generations of students.

One cannot discuss Caroline’s work without mention of her aptly named and lavishly illustrated book Indra’s Pearls written jointly with David Mumford and David Wright. This widely praised book describes everything that is needed to understand and draw limit sets of two-generator Kleinian groups, including basic computer algorithms needed to make the pictures. Written so that very little technical knowledge is required and beautifully illustrated with quirky figures, precise geometric drawings, and intricate computer-generated figures, its appeal extends not just to experts in the field, but also to undergraduates and amateur mathematicians. In particular it explains and illustrates the many extraordinarily striking and intricate patterns that arise in these limit sets, such as those shown in Figures 6 and 10, and it touches on some of the combinatorial ideas describing the possible cutting sequences for simple geodesics used in her subsequent work with Linda Keen.

Another important contribution of Caroline is her substantial service to the mathematical community at large. She has an immensely influential track record in opening up the subject to underrepresented groups, particularly for women. She was a founding member of European Women in Mathematics (EWM) in 1986 and has held senior roles in the EMS Women in Math Committee and the IMU Committee for Women in Mathematics. Together with other senior women, such as her long-term collaborators Joan Birman and Linda Keen, the effect that Caroline has had on improving gender equality in mathematics has been of great benefit to us all.

On the broader front, Caroline has made many significant contributions to organizations that support the mathematical community. She has given many years of dedicated service to the London Mathematical Society, the European Math Society, and the IMU. Within the LMS she has held several important roles, most notably, as already mentioned, serving as its president from 2017 to 2019. She twice served on mathematics panels for the UK Research Excellence Framework (REF). She has also been significantly involved in the Isaac Newton Institute, in recognition of which she was recently (2022) made an Honorary Fellow of the Institute.

Figure 10.

Computer rendering by David Wright of the limit set of a two generator Kleinian group based on an original hand drawing by Fricke and Klein; see Fig. 156 in Vorlesungen über die Theorie der automorphen Functionen, Vol. 1, Leipzig 1897.

6. Conclusion

Caroline has made valuable and fundamental contributions to hyperbolic geometry, in particular, the geometry of hyperbolic surfaces and three manifolds. She has introduced important ideas, elucidating and clarifying connections between different aspects of hyperbolic geometry and symbolic dynamics. However, her contributions to the field go far beyond the mathematical aspects. She has been an influential role model who has fostered and nurtured a generation of young mathematicians who have gone on to make significant contributions in their own right. She has been particularly supportive of women mathematicians and other mathematicians from disadvantaged groups, both from official and unofficial positions. She has given numerous public talks which have contributed to the general public’s understanding of the work of research mathematicians. She has also organized and co-organized several major conferences, workshops, and meetings in her field, bringing together leading experts and generating a very vibrant and collegial atmosphere for research. She personally ensured that all participants, whatever their background, feel welcomed and part of the proceedings. In particular, she has been instrumental in fostering connections between European, American, and Asian researchers, strengthening in particular the Europe/Asia mathematical ties. Her efforts have helped create an inclusive and supportive atmosphere in the field, making it a very congenial and pleasant area to work in.