What Can We Say About “Math/Art”?

“Math/art” is becoming a standard term, but what exactly is it or should it be? Mathematical fields tend to mature over time, typically beginning with examples studied in isolation, then connections are observed, generalizations are noted, insightful essences are formalized, and ultimately organizing ideas are articulated that clarify the entire subject. In the field of mathematical art there are many fascinating examples about which interesting things can be said, with myriad connections apparent, but the practice of making mathematical artworks has not been organized into any coherent framework. I will not attempt anything so grand here, but I will suggest that mathematicians should be looking harder at mathematical art, both creating more examples and examining them critically. There are many unknowns to clarify and formalize. It is not even clear where to place the field: is it a specific branch of applied mathematics or a separate discipline that emerged from math and art? Studying interesting examples is a key step in this process of maturation.

Figure 2.

Jasper Johns, Numbers. The composition of this painting features a $2\times 5$ array of the digits 0 through 9. The numbers seem to be employed merely as neutral objects for carrying the artist’s experiments with color, but they are positioned in a specific sequential structure and the dimensions 2 and 5 derive from factoring 10, raising the question of whether this should be considered “mathematical” art.

I consider myself an applied mathematician and sculptor, employing mathematical techniques and ideas in creating geometric art. Much of my time is spent designing and constructing physical artifacts that I offer to the world as aesthetic objects in the category informally called “math/art.” My hope is that viewers, mathematically trained or not, will find these works to be worthy of appreciation. The mathematician in me enjoys discovering, thinking about, and communicating engaging patterns and relationships embodied in sculptural form. The artist in me delights in the self-expression, beauty, and cultural enrichment associated with creative artworks.

From a human perspective I find no contradiction, rather a great resonance, in the blending of mathematics with fine art. It is a central part of my life. Yet when attempting any rational introspection into the nature and power of mathematical art, one is immediately stymied by the fact that the subject seems ill-suited to our usual tools of formal analysis. One can’t even define “art” in the rigorous way that elementary mathematical practice would require. And even without a universal definition of “art,” if we agree that a particular object is art, people may still disagree on whether it is also “mathematical art.”

Without firm foundations, is there any substance here to interest a mathematician? I claim Yes, but one cannot hope to approach the topic as in a textbook with definitions and theorems already laid out. Instead, one must see it more like a challenge at a group problem-solving session, where one ponders examples and counter-examples and enjoys the communal process of beginning to sort through and make sense of an initially confusing cloud of ideas. There are intellectual and aesthetic treasures to be found in the world of math/art, though it may not be easy to express them in rigorous terms. Trained mathematicians are well positioned not only to appreciate the field and move it forward, but also to articulate what it is that makes mathematical art such a worthy human endeavor.

Figure 3.

Sol Lewitt, Incomplete Open Cubes. An example of twentieth-century minimalist and serialist art, this type of work led many contemporary viewers to ask “Is it art?” The artist poses a puzzle by presenting an answer and leaving the viewer to discover the question. A mathematician can phrase it as enumerating all 122 connected subsets of the twelve edges of a cube that span $\mathbb{R}^3$ and have cardinality less than twelve, modulo rigid rotations.

For centuries philosophers have debated varying definitions of art without resolution. Proposed essential characteristics have involved aesthetics (a sufficient degree of beauty), or mimetics (the quality of representation of some subject matter), or technical achievement (original, one-of-a-kind, hand-made mastery), or an affective relationship to the viewer (being thought-provoking or emotionally moving rather than functional), or even the role of culture and institutions (anything in a “museum” by an “artist” is art). For an entry into this formidable literature see 1. However, such attempts appear to be doomed to failure given the wide range of accepted art objects and categories found throughout the classical, contemporary, and multicultural domains and given the individual variation in how people gauge the artistry of particular examples. Mathematicians, with their professional expertise in making and testing deeply thought-out definitions, are no doubt particularly adept at finding faults in any proposed necessary and sufficient conditions claimed to circumscribe the set of objects to be labeled “art.”

Figure 4.

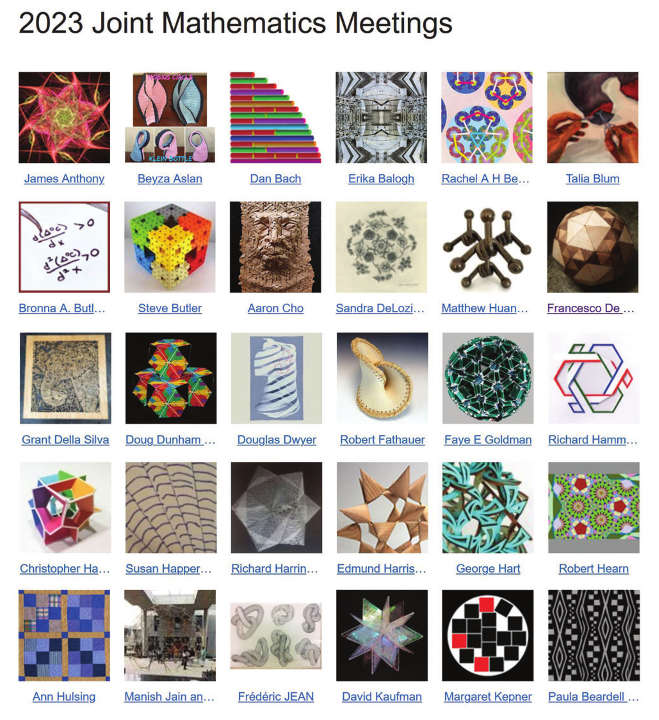
Front page of the Joint Math Meetings 2023 Art Gallery web page. An assortment of media and mathematical topics are represented in the curated art exhibition galleries on display at the Joint Math Meetings and the Bridges Conference each year. The various works can be considered to be art, craft, design, models, or visualization.

If we accept that there is no unified essence of “art” to be approached with the mathematician’s definition-theorem-proof mindset, how then should we proceed? And toward what goal? For years, I have considered writing a “Mathematical Art Manifesto” akin to the twentieth century’s celebrated “Cubist Manifesto” and “Surrealist Manifesto” (and dozens of others). Such documents typically spawn from a coherent community trying to prescribe the values and motives of an emerging art movement. For starters, do we have a relevant community?

I am hardly alone as a geometric sculptor; there is a large supportive math/art community. The annual art exhibition at the Joint Math Meetings 2, the Bridges Conference on Mathematics and Art 3, the Journal of Mathematics and the Arts 4, the MAA special interest group in the arts (SIGMAA-ARTS) 5, the semester-long ICERM workshop on Illustrating Mathematics 67, and a great many published books and articles 8 all attest to the vibrant health of the field. A large community is passionately creating and appreciating mathematical art. This consists largely of people who are trained to at least the university level in mathematics, but also includes a wide range of math lovers, educators, and artists who find a natural affinity to patterns and structures expressed in a creative manner. Should some type of Mathematical Art Manifesto be our formal goal? My view is that the congregation has not yet reached a level of consensus on the core values of mathematical art 9.

(As an aside, I should point out that this essay focuses on math/art creation and ignores other thrusts in this community such as the art historian’s perspective on the history of connections between math and art 10, statistical analysis of unsigned art via “stylometry” to determine authorship 11, or studies that interpret what pure mathematicians do to be an artform with the medium being ideas 12.)

As a professional geometric sculptor with a degree in mathematics, deeply involved in the community, I can claim some insight into the field. I have been an associate editor for the Journal of Mathematics and the Arts since its founding. I have been centrally involved with the Bridges Conference since its inception over 25 years ago and have served as president of the Bridges Organization for the past seven years, bringing together hundreds of participants from dozens of countries. I cofounded the Museum of Mathematics in New York City, brought in the artists whose works decorate it, and specified that it must contain an art gallery space for changing exhibits. I know personally a sizable fraction of the community and have no doubt read (and/or reviewed) over a thousand academic papers on the subject.

Figure 5.

Albrecht Durer, Melancholia I. This enigmatic engraving includes a $4\times 4$ magic square, a drawing compass, a sphere, a mysterious polyhedron, and other symbolic references. Various attempts have been made to explain the specific polyhedral shape. Is it a cube elongated into a rhombohedron, then truncated to be inscribable in a sphere? What might it symbolize?

One entry into an understanding of mathematical art is to look at the works that have been accepted into the curated mathematical art exhibitions at the JMM and the Bridges Conference or described in peer-reviewed conference and journal papers. One finds a wide variety of media and subject matter, including computer-generated renderings of fractals, hand-drawn tessellated images inspired by M. C. Escher, or beautiful physical models of mathematical objects such as lattices, knots, topological surfaces, or polyhedra. There are geometric origami, intricately patterned quilts, and amazing handmade examples of beadwork, crochet, knitting, and tatting, each with an underlying mathematical story. In addition to new media such as 3D printing and computer-controlled wood carving, many traditional fine art media, such as oil painting, watercolor, encaustic, ceramics, or block printing are adapted to illustrating mathematical ideas. A knowledgeable viewer will discern inspiration in these works from countless mathematical gems, such as Fibonacci numbers, the Pythagorean theorem, integer factorizations, the seventeen wallpaper groups, concepts of infinity, and much more.

I am regularly impressed with some of the new works presented in these venues, but we must be clear that these efforts are not of interest to world-class fine art museums or high-ticket auction houses. The community that produces this math/art is its own most enthusiastic audience. One must wonder why.

It is clear that in our culture some artworks are more difficult to appreciate than others. Twentieth-century visual art and music is notoriously opaque for some people, often requiring a more educated eye or ear. Lovers of traditional European academic art or Impressionism may draw the line at cubism, dadaism, expressionism, or more avant-garde conceptual art. Twentieth-century artists such as Max Bill, Sol Lewitt, and M. C. Escher were infusing mathematical ideas into their work at a time when engaging with art began to require more active mental involvement.

Figure 6.

Anish Kapoor, Turning the World Upside Down, Jerusalem. This monumental stainless steel sculpture is highly polished to a mirror finish. A mathematician wonders if it is a precise hyperboloid and if so, what optical properties such a quartic surface might display. Installed in Jerusalem, it is interesting that the inverting effect of the mirror literally shows heaven on earth (and vice versa).

Is it possible that mathematical art is simply too hard to understand without the proper education? A quilt containing a visual reference to Cayley tables could be as thematically inscrutable to nonmathematical viewers as a classical painting of a woman holding a swan will be to viewers unfamiliar with Roman mythology. Given the stereotypical “I don’t understand math” sentiment that is not uncommon in our culture, it is tempting to propose that this content issue limits the audience for math/art. While it is certainly true that the inspiration for some mathematical art can not be appreciated by everyone, this is not the whole story. Firstly, even many professional mathematicians who are in a position to understand mathematical ideas are not drawn to works of the math/art community. Secondly, a classical painting of Leda and The Swan may be widely appreciated as art for its sensuous surfaces, formal composition, or masterful brushwork, even if the viewer is unfamiliar with the mythological story. And in the same way one expects worthy mathematical art to be recognizable for its form, craftsmanship, aesthetics or other properties, even if an analytical understanding requires explanation. So unfamiliar mathematical references are not the major difficulty here.

The bigger issue in the world of math/art, I feel, is that much of what is presented in our art exhibitions and publications is not truly “fine art.” Of course, without a formal definition of art I cannot rigorously support this claim. But it is evidently justified by observing the accepted authorities concerning art: the fine art institutions such as museums, galleries, auction houses, and university art departments. The sad truth is that no experts from these organizations are rushing over to our mathematical art exhibitions and being impressed by what they find. We must admit that in terms of their culturally accepted notions of art, something is lacking.

Figure 7.

Kenneth Snelson, Needle Tower. Snelson conquers infinity with a series of modules that are proportionally smaller along the height of the 26-meter sculpture. The viewer misinterprets them as identical and so imagines the structure as extending to the vanishing point. In this “tensegrity” design, compressive elements never touch, so that the weight of the upper beams is supported along a chain of alternating compressive and tensional elements.

This judgment confirms my view that the works presented in the Bridges Conference, the JMM exhibition, and many publications of the math/art community are largely craft, design, models, and visualization, not fine art. But there is nothing wrong with that. An interesting and original object might be considered craft instead of art because it can be reproduced by competent workers following step-by-step instructions. It might be considered design instead of art because it is a digitally printed graphic or is robotically fabricated by a 3D printer. It might be considered a model instead of art because it displays casual craftsmanship and seems most suitable for education. It might be considered visualization instead of art because it originated functionally as an aid for explaining a technical fine point. These characteristics do not make an object less interesting or less valuable within our community, but they may distance the object from accepted notions of fine art.

To reconcile these issues, perhaps what we call an “Art Exhibition” should be rebranded as something like “Exhibition of Mathematical Art, Craft, Design, Models, and Visualization.” This conveniently covers the entire collection without having to be definitionally specific about individual items. Beyond any benefits of self-honesty, this labelling might aid us in appearing more modest to any fine art communities that consider our math/art to be below their artistic standards. A venue that is unwilling to present our works under the rubric “Art” might be happy to display it if labelled less grandiosely.

Figure 8.

Max Bill, Fifteen Variations on a Single Theme, (Variation 1). In a series of lithographs, Max Bill explores constructions based on a nested sequence of regular polygons, decreasing from eight to three sides while sharing a common edge length. A mathematically inclined viewer will want to work out the rule that determines on which side of each polygon the next one is attached.

Artists generally aim to communicate something to their viewers. In contemporary fine art, the message is often a social or political viewpoint, with the artist daring to push boundaries and speak truths not otherwise heard. Math/art is characteristically tamer. Our artist statements typically indicate an interest in communicating mathematical truths with formal or aesthetic appeal. Our exhibition and publication venues promote the sharing of creative works that inform and inspire a specific well-educated community. If this content isn’t being more widely received, it might be argued that we need to find a way to strengthen and clarify our messages, for certainly mathematician artists have a wealth of fascinating raw material available as intellectual inspiration. Whether or not any particular work meets anyone’s particular notion of “fine art” is irrelevant to the community’s larger purpose in aspiring to create art while communicating something of the wonders of mathematics. I am truly delighted to be part of a community that works in a heartfelt manner to create new forms of art and supports each other in this endeavour.

All cultures have found ways to combine mathematics and art, whether it is a hand-pinched frieze pattern along the rim of an ancient clay vessel or an algorithmically generated aperiodic monotile tessellation laser-cut from plastic polymer. Math and art are essential parts of being human. They are powerful languages and tools for communicating and making sense of the world. So it is perfectly natural that our community of math lovers and professional mathematicians is developing art that reflects our own interests and culture. The themes found in mathematical art often embody the kinds of patterns and structures that have brought joy to mathematical thinkers through the ages.

Mathematics appeals because of the delights to be found in rigorous reasoning and understanding with clarity. I believe mathematical art succeeds in our community because it alludes in various ways to these same pleasures. When art mimetically suggests objects and relationships in some Platonic world, those delights may be evoked for viewers who have spent enough time in that realm to understand the reference. A painting that simply portrays a triangle or, say, the digit zero might seem to have a “mathematical” subject to a nonmathematician, but an isolated reference of that sort is unlikely to reach deeply enough into the graph of logical relationships to evoke any joy in a mathematically educated viewer. The art that is mathematical art must bring to mind a landscape of mathematical pleasure.

Figure 9.

Ceramic tiling from the Alhambra palace, in Granada, Spain. Tessellations and frieze patterns are a staple of geometric art across many cultures. This fourteenth- or fifteenth-century example illustrates what is called the 333 orbifold type (in the Thurston-Conway notation) because there are three different types of centers of 3-fold rotation.

The works produced in our community that I characterize as craft, design, models, and visualization also evoke these mathematical landscapes. This is part of our motivation for creating them and helps explains why we are our own best audience. These objects often are created with another purpose as well: education. Many of us are teachers accustomed to taking every opportunity to share our knowledge. Math/art is often used as a hook to engage students in new topics. After they are invested emotionally, mathematical conversations are a natural way for a teacher to gently introduce the technicalities. If one’s definition of “fine art” requires that it be nonfunctional, this utilitarian genesis seems to preclude such objects from being art, but no matter, as this pedagogical math/art may still be inspiring, engaging, and thought provoking.

So math/art might not be a formalizable branch of mathematics and it might not actually be art, in which case it may be a separate discipline emerging between math and art. The “bridge” that the Bridges Conference makes between math and art might best be visualized as stopping over at a volcanic island rising between the two lands. The inhabitants of this ground are developing a culture, tradition, and corpus of work with its own internal logic, and growing a garden of hybrid varieties yet to be fully sorted out. We should all revel in this flowering, even if only a fraction of it reaches a level of “art.”

I encourage everyone to aim for making art, especially mathematicians. Feeling the joy of creation is enormously rewarding. It is an authentic form of self-expression that lets you discover things within yourself and that gives you a powerful channel for communicating to a new audience. Mathematicians in particular are attuned to fascinating ideas that might be shown in original artistic forms. This is easier said than done, of course, as there are many conceptual, material, and expressive challenges, but mathematicians are adept at solving difficult problems. I expect that anyone who enjoys creative mathematics will also enjoy exploring some domain of the arts in which they can be equally creative. Along the way, you might ask yourself “is this really art?” and try to articulate an answer. Work out the details of your own mathematical art manifesto as you push yourself to raise the bar of your artistry.

For me, creating sculpture is a compulsion. I might try to rationalize it as educational, I might be gratified to receive kind words from an appreciative audience, and I might enjoy the profit of making a sale, but I do it as a compulsive behavior. It is a therapy that soothes some inner need. I work in a haze of healthy confusion about the exact nature of mathematical art, but I don’t need a formal framework to know that envisioning new designs and bringing them to reality is somehow saying something beyond words. Finishing a new sculpture is as satisfying as solving a difficult problem, when one’s thoughts crystallize and the fog becomes clarity.

For me, mathematics is a source of great intellectual joy, to be shared as widely as possible, whereas art is the highest purpose of being human. Art can uplift the spirit or invite introspection as it communicates deeper meanings. A world rich in art is full of ideas and inspiration at every turn. I trust that as society evolves, more and more people will be freed to create art. And as a fundamental humanist expression, the scope of art needs to be enriched by the viewpoint of mathematicians. Those who have journeyed through mathematical lands have unique stories to tell of what they found and how they now see the world. I look forward to sampling these tales as more mathematicians become engaged in creating art. And as examples accrue, these discussions will continue, various organizing principles will start to emerge, and our understanding of mathematical art can only mature.