Magical Mathematics - A Tribute to Martin Gardner
Perhaps no one has done more to make the world aware of mathematics than Martin Gardner...
 Joseph Malkevitch
Joseph Malkevitch
York College (CUNY)
Email Joseph Malkevitch
Introduction
Who are the people who write about mathematics in the clearest way? One might expect that such people are trained mathematicians - those who have majored in mathematics and gone on to get a doctorate in mathematics. While there are many wonderfully talented expositors of mathematics who are graduate school trained mathematicians, it turns out that one of the greatest expositor of mathematics, for me perhaps the greatest, was Martin Gardner. Gardner in a sense "became" a mathematician but did not "train" to do so.

Martin Gardner in 1932 (Courtesy of Wikipedia)
Many mathematicians see their subject as magical - having unexpected surprises and delights. However, all too often the magic of mathematics is lost on those who have not chosen mathematics or a related subject as a career. Perhaps no one has done more to bridge the gap between the sometimes lukewarm public view of mathematics and internal views of mathematics as a magical subject than Martin Gardner. Here I would like to provide a tribute to Martin Gardner for his efforts to popularize mathematics, as well as to his success in convincing many people of the beauty, applicability, joys and magic of mathematics. And I am not alone--this month mathematics pays tribute to him with "Mathematics, Magic, & Mystery," the theme for Mathematics Awareness Month (April) 2014. Perhaps no one has done more to make the world aware of mathematics than Martin Gardner.
Who was Martin Gardner?
Martin Gardner was born October 21, 1914 in Tulsa, Oklahoma. and died on May 22, 2010 not that far from where he was born, in Norman, Oklahoma. During his long life he lived in and traveled to many places but wherever he was, he seemed to carry his pen with him. What were the forces that molded this author of over 60 hardcover books?
Gardner's father had a doctorate degree in geology and his mother at one time taught in elementary school but eventually stayed at home to raise her three children. Perhaps an early source of Gardner's interest in puzzles was the gift by his father of the well-known Cylopedia of Puzzles by Sam Loyd (1841-1911). Loyd was famous for creating mathematical and chess puzzles, and Gardner showed a keen interest in his writings in problems related to chess. Of his experiences in high school Gardner wrote:
I was very good at math in high school. In fact, it and physics were the only subjects in which I got good grades. I was bored to death by the other classes.
Gardner's hope was to study physics after graduating high school at the California Institute of Technology (CIT) but to do so required having two years of experience in college. Gardner went to the University of Chicago in preparation for going to CIT. At Chicago he become interested in philosophy and stayed there to get an undergraduate degree in philosophy in 1936. It was the Depression, but Gardner found a variety of jobs (including working as a reporter for the Tulsa Tribune) before he joined the Navy to fight in World War II. After returning from the War, Gardner returned to do graduate work in philosophy at the University of Chicago but did not finish a graduate degree.
Eventually he made his way to New York City (1947) and became involved with writing for and editing magazines, as well as book writing. One of his early books was Fads and Fallacies in the Name of Science. Though he did not have an advanced degree in mathematics, Gardner won one of mathematics' most prestigious awards, the Leroy P. Steele Prize. Here is the citation for his 1987 prize:
To Martin Gardner for his many books and articles on mathematics and particularly for his column "Mathematical Games" in Scientific American.

(Photo of Martin Gardner)
Comments?
Gardner's columns and books
What put Gardner on the mathematical map was his association with Scientific American magazine, which had started publication in 1845. In December, 1956 Gardner wrote an article for Scientific American about an intriguing family of geometrical objects known as flexagons.
A flexagon is a "flat" geometric shape that can be folded from a strip of paper (cardboard) which shows various panels, which can be changed to other panels by "flexing" the shape. The diagram below, through a series of images, shows how colored triangles can be folded into a hexagonal shape which can be "flexed" into other positions which show colors after flexing that did not appear initially. The "moves" progress through a seemingly mysterious/magical collection of patterns. Sometimes numbers or fortunes are written on different panels of flexagons, making their use a perennial source of entertainment and wonder.
Diagrams illustrating a flexagon (Courtesy of Wikipedia)
Another example of a flexagon in two positions is displayed below.

Two positions of a flexagon (Courtesy of Wikipedia)
Flexagons have a rich history, having been initially discovered by the mathematician Arthur Harold Stone. Stone studied mathematics at Princeton and it was while he was there that he discovered flexagons. The story goes that having come from England he trimmed the larger British paper size down and his foldings of the "extra strips" were responsible for the birth of flexagons. Flexagons soon attracted the attention of some of his fellow graduate students at Princeton - John Tukey (famous for his development of the fast Fourier transform (FFT) and major work in statistics), Bryant Tuckerman (topologist), and Richard Feynman (distinguished physicist, and inventor of Feynman diagrams).
(Photograph of Arthur Stone, courtesy of Stuart Anderson)
Gardner's column in Scientific American attracted enough attention that Scientific American offered him the opportunity to write a "Mathematical Games" column on a regular basis. Starting with the January 1957 issue of the magazine, Martin Gardner began a 25-year run of writing columns for Scientific American. These columns eventually were collected into many books that were a great source of interesting mathematics for many mathematicians, not to mention the general public.
One of the companies that published Gardner's books was W.H. Freeman and Company. The mathematics editor at Freeman who did much to market and popularize the work of Gardner was the late (2003) Jeremiah J. Lyons, known to his friends as Jerry. Jerry, like Gardner, did not start out in mathematics but did graduate work in English. He then went on to sell mathematics books for Prindle Weber and Schmidt, and eventually made his way to Freeman as an editor. After leaving Freeman he had a long career with Springer (first Springer-Verlag) as a mathematics editor and publisher. It was his background initially as a salesman and eventually as an editor and publisher that built his fine sense of when people had special things to say and could say it in a special way, as was the case for Martin Gardner. The photograph below shows Gardner with Jerry Lyons and the distinguished geometer Thomas Banchoff (also a president of the MAA).

Photo of Jeremiah (Jerry) Lyons, Martin Gardner, and Thomas Banchoff (Courtesy of Tom Banchoff)
Gardner drew on a large number of mathematicians over the years for ideas and inspirations for his columns. Below is a small gallery of distinguished mathematicians who inspired his work and to whom he dedicated some of his books.
(Photo of John Horton Conway)

(Photo of Ronald Graham)

(Photo of Donald Knuth)
The range of wonderful problems, examples, and theorems that Gardner treated over the years is enormous. They include ideas from geometry, algebra, number theory, graph theory, topology, and knot theory, to name but a few. Characteristically, his columns were self-contained and were light on the mathematical notation that makes many people have a distaste for mathematics. Not having any easy way to pick among many gems, I am choosing a few that show some magical or intuitive aspects, and one that shows Gardner's playfulness.
Comments?
Birthday surprise
We have mentioned that Gardner was born on October 21. He shared October 21st as a birthday with a variety of people who are perhaps better known than he: Benjamin Netanyahu, Kim Khardashian, Dizzy Gillespie and Malcolm Arnold. However, for those within mathematics who were born and died on this day, Gardner may hold his own in recognizability.
1687 : Nicolaus(I) Bernoulli
1823 : Betti
1855 : Guccia
1882 : Vandiver
1893 : Ferrar
1914 : Gardner
Mathematicians who died on the same day as Gardner :
1881 : Heine
1969 : Sierpinski
2000 : Struik
2002 : Bernhard Neumann
Martin Gardner had a playful personality so it might not "offend" the man who wrote lots of materials about the exploits of Dr. Matrix to be listed with others who promoted mathematics who were born or died on the same day that he was born or died.
One of Martin Gardner's first compendiums of columns, a book published from the columns that he wrote for Scientific American magazine, was the collection: Hexaflexagons and other Mathematical Diversions: The First Scientific American Book of Puzzles and Games. One of the chapters of this book was entitled Probability Paradoxes. This chapter, among other surprising examples, discusses a phenomenon that still amazes and mystifies people, even after they have seen the proof and observed its success in action.
I am at a party with a group of people. What is the probability that there are two people (or more) who share a birthday? Note this is not the same as asking for the probability that there is another person who has the same birthday as I do. Here is the question put in more specific terms where we can construct a mathematical model:
If one is at a party with k people, what is the smallest value of k such that there is at least a 50-50 (equal) chance that two or more of the people have the same birthday?
Suppose we wanted to know for a group of 4 people, what the probability is that at least 2 of the 4 have the same birthday. In a non-leap year there are 365 different days that people can have birthdays. For simplicity we will assume that the 4 people involved have their birthdays on one of these 365 days. Now if 2 of these people are twins then they would in all likelihood have the same day for their birthday (though they might have birthdays on consecutive days). This is because the birthdays of twins are not "independent" of each other. For simplicity we will assume that the birthdays of the 4 people are independent of each other, and they are equally likely to be on any particular day. Now in fact, the number of people who are born each year on a particular day is not exactly the same. But we will assume that the probability that someone will be born on day "i" of the 365 days in the year (that is, we number the days of the year from 1 to 365) is 1/365. (Some births arise from "induced" labors and such induced births usually don't happen on weekends or on holidays that occur in the middle of the week. So in the real world the probability that one is a randomly selected person to be born on July 4th may not be 1/365.)
Now what is the probability that the first 2 of people in the group of 4 have different birthdays? The first person has some birthday, whatever day it is. If the second person has a different birthday, this person's birthday can be any of the 364 days other than that of the first person. Since each day has the same probability of 1/365, the probability that the second person has one of these other 364 days as his/her birthday is 364/365. If X and Y are independent events then the probability that both X and Y occur, where the probability of X is P(X) and the probability of Y is P(Y), is P(X) times P(Y) (see more below about this). The first person has some birthday, so the probability of this is 365/365 or 1. So the probability that we have both people with different birthdays is:
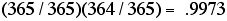
What about the first 3 people of the 4? For them to have different birthdays the third person can have as a birthday any of the 363 days which are different from those of the first 2 people. Using independence, the probability these 3 people have different birthdays is:
Again we multiply because the birthdays of the 3 people so far are independent of each other. Finally, what is the probability that all 4 people have different birthdays? This is the probability that the 4th person has a different day for his/her birthday from the first 3. So we have
as the probability that the 4 people have different birthdays. What about the probability that at least 2 of these 4 people have the same birthday? If I know the probability of Z occurring, P(Z), the probability of Z not occurring is 1 - P(Z). The probability of the "complement" of an event Z (the event not happening) is one minus the probability of Z.
Hence the probability that at least 2 of 4 people will have the same birthday is obtained by subtracting .9836 from 1:
This is about 2% of the time. Not very likely. But perhaps you have noticed the pattern of the relatively fast decline in the values of the products above. If instead of doing this calculation for 4 people we do it for 10 people we get the value that at least 2 people will have the same birthday is:
For 10 people, there is about a 12 percent chance that at least 2 of them will have the same birthday.
Amazingly, by the time we get to 23 people, the probability that at least 2 of them will have the same birthday is:

which is more than 50%.
Thus, the perpetually surprising reality is that in a "random" group of 23 or more people at least two of them will have the same birthday. For a party where few people know each other, one way to break the ice might be to locate 2 people who have the same birthday. Of course there are other ways to set this discussion. Consider the set of Vice-Presidents of the United States. Since there have been more than 23 such people there is quite a high chance that 2 of them will have had the same birthday. If you are a student sitting in a class of 23 or more students, there is more than a 50-50 chance that 2 students in the class will have the same birthday.
What tools did we use to derive the result above? It was based on the multiplication principle for independent events. Intuitively, the idea of independence is when events do not "affect" each other. What I do when I flip a "fair" coin does not typically affect the result of the next flip of that coin. (There are people who practice flipping coins so that they always get heads. With practice one can accomplish this.)
But there are situations where what happens first affects what happens later. This involves the notion of conditional probability. Suppose I have a bag with 3 balls, 2 of which are black and one is white. Suppose I draw one ball after another from the bag without replacing the earlier selected balls. I can ask what is the probability that the first of the two balls I draw is black? Do you see why the answer is 2/3? Now suppose I look at the first ball and see that the ball is black. What is the chance now I get two black balls? This time the answer is 1/2. If the first ball had been white, what is the chance that the first two balls are black? The answer is that this cannot happen, so the result must have probability 0.
The way these ideas are treated is as follows: If X is an event we say that the probability of X is P(X). So, how might we deal with the probability that event X will occur given that event Y has occurred? And what about the probability that Y will occur given X has occurred? Clearly these are sometimes different!
So let us "invent a notation" for such "conditional" probability occurrences. We will write: P(X|Y) to denote the probability that X occurs given that Y has occurred. Thus, P(Y|X) will denote the probability that Y occurs given that X has occurred.
How can one calculate P(X|Y)? We will make the following "definition."
P(X|Y) = P(X and Y both occur)/P(Y). (*)
This definition is motivated by the diagram shown:
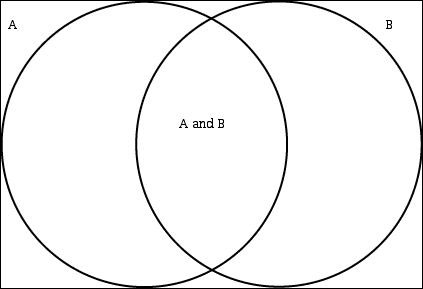
Events A and B are represented by the circles, and outcomes that have properties A and B are shown by the circle's overlap. If we want to know the probability of B occurring given that A has occurred, P(B|A), we can restrict our attention to things inside A since we know A occurred. Now to find out what chance there is that B occurred given A occurred means we want to see "what part" of A is represented by the overlap of A with B. This is exactly what (*) says, and so this is the motivation for this definition.
If A and B are independent, that is, they do not affect each other's occurrence, then we should have that P(A|B) should be equal to P(A). From (*) this means that P(A and B) be equal to the product of P(A) and P(B). This is the multiplication rule for independent event probabilities.
Using the notations developed above, here are the answers to the questions above, as well as some other probabilities, about probabilities of drawing 2 balls one after another from a bag with 3 balls, 2 of which are black.: P(first two balls are black) = 1/3; P(first ball is black) = 2/3, P(two balls are black | first ball is black) =1/2, P(first ball is black | first two balls are black) = 1, P ( first two balls are black | first ball is white) = 0, P (first ball is white | first two balls are black) = 0..
The "birthday surprise" is but one of many situations in which people's intuition for the nature of probability has to be "trained." Another example is that when one is dealing with a quite reliable test for an ailment (disease) which occurs rarely, the probability when a patient's test is positive that the patient does not actually have the disease (false positives) is quite high.
Comments?
A map requiring 5 colors?
Martin Gardner had a playful streak and often had columns which had whimsical goals. In his Scientific American column of April 1975 he showed a plane map which purportedly required 5 colors to color the faces. The rule is that if two regions share an edge they should get different colors.
(Plane map requiring 5 colors?)
Image courtesy of Wolfram
The face-coloring problem for maps asks: What is the minimum number of colors with which one can color the regions of a map drawn in the plane so that regions (faces) which share an edge receive different colors? This problem, which has a long history, resulted in one of the most famous "false proofs" in the history of mathematics. Alfred Kempe, a lawyer by profession but with a significant record of accomplishments as a mathematician, claimed to have proved what came to be called the 4-color conjecture. This conjecture asserted that any plane map could be colored with 4 or fewer colors.

(Alfred Kempe)
Kempe's proof had a subtle error and that error was pointed out by Heawood, who showed that one could prove that plane maps could always be 5-colored.

(Photo of Percy Heawood)
The proof of Kenneth Appel and Wolfgang Haken, that any planar map could be 4-colored, was apparently completed in 1976 and did not appear in print until a year later. So Gardner's column occupied the niche of high interest in the status of the conjecture that pre-dated the appearance of a proof. Some controversy accompanied the proof because it involved the use of a computer in a way that precluded humans being able to follow all of the steps. While many mathematicians were not bothered by this aspect of what Haken and Appel did, there was considerable discussion of the matter by mathematicians and others. Eventually, a simpler proof than that found by Appel and Haken appeared by Neil Roberston, Paul Seymour, Daniel Sanders and Robin Thomas. However, this proof, while more streamlined than the earlier one, still involved the use of a computer.
So yes, Gardner's column was an April Fools' joke. Here is a coloring of the challenge map above, designed by William McGregor, which was found by Stan Wagon. While all plane maps are 4-colorable, finding a 4-coloring for a particular map is often a challenge.

(4-coloring by Stan Wagon of Gardner's April Fools' map)
Image courtesy of Wolfram
Comments?
Joseph Malkewitch (sic) meets Martin Gardner
I was in the audience to hear Martin Gardner but I never met him in person. However, in a variety of ways our paths crossed. Gardner first came to my attention when as a teen on a trip to Florida, an automobile accident stranded me and my parents in Winter Haven, Florida, while our car was being repaired. My "lifesaver" for this period was a local library within walking distance of where we were staying, which was where I got my first introduction to Scientific American magazine and the columns of Martin Gardner. On returning to NY I started a subscription to Scientific American, and my subscription has never lapsed. Eventually, when I had large enough living quarters I started to acquire Gardner's books. HIs books were initially easier to consult than trying to go back to his Scientific American columns. However, there was also the fact that when his Scientific American columns appeared in book form, Gardner updated information about the mathematics in the columns with additional details about what was new about the problem since it had initially been published. One wonderful aspect of Gardner's Scientific American columns was that he and an "army" of appreciative, motivated and talented people (including some who were professional mathematicians) thought about the questions that he raised. In some cases his columns dealt with issues which, at the time he wrote about them, were not fully understood. So his books allowed him the opportunity to "update" columns with new ideas and results when the columns were collected for reprinting.
I also had an indirect "meeting" with Martin Gardner. While I was a graduate student at the University of Wisconsin in Madison, I became interested in what have come to be called Eberhard Type Theorems, in honor of the blind 19th century geometer Victor Eberhard. Eberhard's work was "rediscovered" by the geometer Branko Grünbaum, and there are many papers about this topic now in the literature. In conjunction with this I became interested in ways to tile convex polygons with various shapes, in particular with equilateral triangles and squares. The diagram below shows a "patch" of tiles of a portion of the plane which uses only equilateral triangles and squares.
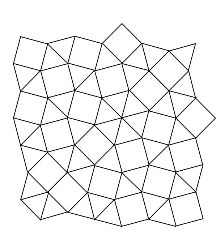
(Patch of tiles which consists of equilateral triangles and squares)
Can you pick out in this tiling corners for convex polygons with 3, 4, 5, and 6 sides? What other values of n are there so that there is a convex polygon with n sides which can be tiled with equilateral triangles and squares all having the same side length? (In thinking about this one can have vertices of the tiling polygons that are not vertices of the convex polygon. For example, above you can find a convex pentagon which is tiled with two squares and a triangle.) The answer to this question is a nice application of some simple ideas from elementary geometry so I submitted it as a problem to Mathematics Magazine. Here is what appeared in November 1968:
707. Proposed by Joseph Malkewitch, University of Wisconsin.
For what values of k is there a convex polygon with k sides which can be
dissected into squares and equilateral triangles which have the same length of side?
The solution by Michael Goldberg appeared in May, 1969. Here is a diagram which shows solutions for n = 3 to n = 12, and it is not hard to show there are no other values of n. There are still some open questions related to the shapes of those n-gons that can occur for some values of n.
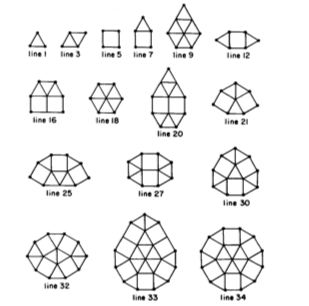
I was very pleased when Martin Gardner picked up on this problem and used it in his book Knotted Doughnuts and the later compendium Colossal Book of Short Puzzles and Problems. However, Joseph Malkewitch is really me! (Vould I lie to you?)
Comments?
Carrying on the Gardner tradition
Gardner fans were disappointed when Gardner no longer continued to write his column for Scientific American. The magazine tried to find a "replacement" for Gardner by having various authors and columns that tried to capture the spirit of Mathematical Games. Eventually, however, Scientific American resigned itself to the fact that Gardner really could not be "replaced!" Happily Gardner continued to provide inspiration for fans with his books (see a partial list in the references).
Fortunately, the spirit of what Gardner started with his columns and books continues via a series of events to remember him and his name. This is done via the conferences and workshops in different locations that have come to be known as Gatherings for Gardner. It is a wonderful tribute to Gardner that what he valued so much will continue to inspire people in the future.
Mathematics is a magical subject and you don't have to be a "trained" mathematician to savor, love, and participate in the magical world of mathematics. As we enjoy Mathematics Awareness Month, we say: Thanks, Martin!

Comments?
References
A list of some of Martin Gardner's books:
1. The Scientific American Book of Puzzles and Diversions (Hexaflexagons and Other Mathematical Diversions: The First 'Scientific American' Book of Puzzles and Games)
2. The Second Scientific American book of Mathematical Puzzles and Diversions
3. New Mathematical Diversions
4. The Numerology of Dr. Matrix
5. The Unexpected Hanging
6. The Sixth Book of Mathematical Games from Scientific American
7. Mathematical Carnival
8. Mathematical Magic Show
9. Mathematical Circus
10. Wheels, Life and other Mathematical Amusements
11. Knotted Doughnuts
12. Time Travel and other Mathematical Bewilderments
13. Penrose Tiles to Trapdoor Ciphers
14. Entertaining Mathematical Puzzles
15. Mathematics Magic and Mystery
16. The Last Recreations
17. The Colossal Book of Mathematics
18. The Colossal Book of Short Puzzles and Problems (ed. Dana Richards)
19. A Gardner's Workout
Other books by Martin Gardner:
Aha! Gotcha
Aha! Insight
The Magic Numbers of Dr. Matrix
The Incredible Dr. Matrix
Logic Machines and Diagrams
The Ambidextrous Universe
Fads and Fallacies in the Name of Science
The Relativity Explosion
The Night is Large
Books that pay homage to Martin Gardner or carry on his tradition:
Cipra, B., and E. Demaine, M. Demaine, T. Rodgers, (eds.) Tribute to a Mathemagican, A.K. Peters, Natick, MA., 2005.
Klarner, D. (ed.), The Mathematical Gardner, Wadsworth, Belmont, CA., 1981. (Reprint by Dover Press.)
Berlekamp, E. and T. Rodgers, (eds.), The Mathemagician and Pied Puzzler, A. K. Peters, Natick, MA., 1999./
Wolfe, D. and T. Rodgers, (eds.), Puzzler's Tribute, A.K. Peters, Natick, MA., 2002.
Martin Gardner's columns and books have been referenced by huge numbers of research papers that involve mathematics. I list only one, which happened to catch my attention because I noticed it as I was writing parts of this column:
Cooper, A. and O. Pikhurko, J. Schmitt, G. Warringron, Martin Gardner's minimum no-3-in-line problem, Amer. Math. Monthly, March, 2014, 121 (2014) 213-221.
Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet can be used to get additional bibliographic information and reviews of some these materials. Some of the items above can be found via the ACM Portal, which also provides bibliographic services.
Comments?
 Joseph Malkevitch
Joseph Malkevitch
York College (CUNY)
Email Joseph Malkevitch



 Joseph Malkevitch
Joseph Malkevitch















