Lost (and found) in space
There are standard references, such as the Sloan Digital Sky Survey, that provide an atlas for the stars. What's needed is a way to search through this enormous atlas to find the view presented by a given image.
My son recently sent me this picture of the comet Neowise that he took from southern California in the summer of 2020.

Photo credit: Sam Austin
I had seen Neowise and knew roughly where it appeared, but being a comet, of course, its position changed over time. I wondered if there was a way to locate precisely where it was at the particular instant this picture was taken.
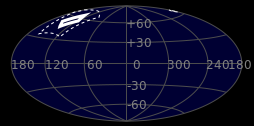
Well, there's an app for that. I uploaded the image to Astrometry.net and learned 36.1533 seconds later that we were looking here:
The image on the left places the picture on the celestial sphere, an imagined distant sphere centered at Earth. The coordinates depict declination (Dec), the angular distance north or south of the celestial equator, a projection of Earth's equator, and right ascension (RA), the angular distance east of the First Point of Ares, a reference point on the celestial equator. A closer view appears on the right where we see that we're looking at a portion of the constellation Ursa Major, which may be more familiar as the Big Dipper.
Here are some more details:
Center (RA, Dec): |
(135.836, 55.212) |
Center (RA, hms): |
09h 03m 20.603s |
Center (Dec, dms): |
+55° 12' 44.873" |
Size: |
16 x 10.7 deg |
Radius: |
9.616 deg |
Pixel scale: |
9.6 arcsec/pixel |
Orientation: |
Up is 313 degrees E of N |
Astrometry.net also labels other features in the picture:
Measuring the positions and motions of celestial bodies falls to the branch of astronomy known as astrometry, and the problem of placing an image into a standard reference, as illustrated above, is called calilbrating the image's astrometry. The work of Astrometry.net, calibrating images without human intervention, is known as auto-calibration.
There are a few reasons why this is an important tool. First, calibrating an image taken by a camera mounted on a spacecraft in a fixed pose can be used to automate the determination of the spacecraft's orientation. Similarly, image calibration can be used to help a telescope track a target as Earth rotates.
Perhaps more importantly, decades of research have created a vast number of astronomical images. Sharing these images with a wide community of researchers is hampered by the fact that the meta-data surrounding these images is often inaccessible, of poor quality, or presented in a variety of formats. Automating the calibration process allows one to construct high quality meta-data in a standard format, enabling astronomical data to be shared and used more easily.
In broad terms, auto-calibration is a search problem similar to Google's internet search engine. There are standard references, such as the Sloan Digital Sky Survey, that provide an atlas for the stars. What's needed is a way to search through this enormous atlas to find the view presented by a given image.
Let's go behind the scenes to understand how Astrometry.net performs this search. There are really two phases. We begin with a known reference, like the Sloan Survey, and create an "index," as we'll soon describe. We only need to do this once so we don't mind committing time and computational power to this task. Next, we develop a means of searching the index to locate a specific image.
The basic idea is to detect certain features in an image and describe them in a way that is both independent of the orientation and scale of the image and easily searchable. The features we will use are configurations of four stars, called quads.
Describing quads
Given an astronomical image, it's fairly straightforward to pick out the brightest stars using standard image processing software. Using the OpenCV software library, I was able to pick out the 100 brightest stars from our original image. To make them more apparent, I reversed the image so that brighter parts of the original image appear darker here.
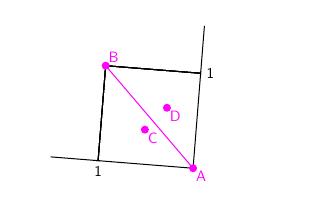
We will construct a description of quads, configurations of four stars, that is independent of their orientation and scale in the image. To illustrate, here's a quad with stars labeled $A$, $B$, $C$, and $D$.
We label the four stars so that $A$ and $B$ are separated by the greatest distance. We then use those two stars to form an orthogonal coordinate system with $A$ at the origin and $B$ at $(1,1)$. We only consider quads for which the other two stars, $C$ and $D$, are within the unit square in this coordinate system.
If $(x_C, y_C)$ and $(x_D, y_D)$ are the coordinates of the interior stars, we associate the four-dimensional point $(x_C, y_C, x_D, y_D)$ to the quad.
Of course, there's some ambiguity in how we label $A$ and $B$. Swapping the labels on $A$ and $B$ performs the transformation: $$ (x_C, y_C, x_D, y_D) \mapsto (1-x_C, 1-y_C, 1-x_D, 1-y_D). $$ We choose the labeling of $A$ and $B$ that gives $x_C + x_D \leq 1$. There are also two choices for how we label $C$ and $D$, and we choose the one with $x_C\leq x_D$. With these choices, the point $(x_C, y_C, x_D, y_D)$ is uniquely associated to the quad. For instance, the quad above is uniquely associated to $(0.36367, 0.53644, 0.61088, 0.32359)$.
This association works well for our application since it doesn't change if the quad appears in a different orientation. For instance, if the quad is translated, rotated, or scaled, we still obtain the same four-dimensional point $(x_C, y_C, x_D, y_D)$.
To create an index, Astrometry.net chooses a collection of quads from a reference, such as the Sloan Survey, that covers the entire sky. As we'll see next, representing quads as four-dimensional points allows us to easily search for specific quads. When presented with an image to be calibrated, we find a set of quads in the image and then search the index for them. When we find a match, it's straightforward to construct the coordinate transformation between the pixels of the image and the celestial sphere.
kd-Trees
Due to noise present in astronomical images, we cannot expect that the four-dimensional point associated to a quad obtained from our image will exactly match a point in the index. Images are distorted, for instance, by the particular optics of a telescope and by the refraction of Earth's atmosphere. If we're given a quad, what we'd really like to do is find all the nearby quads and consider each as a potential match.
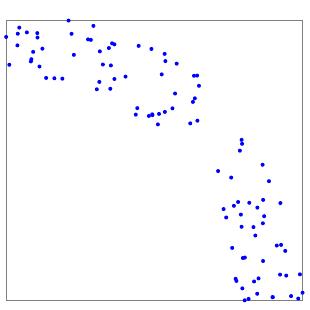
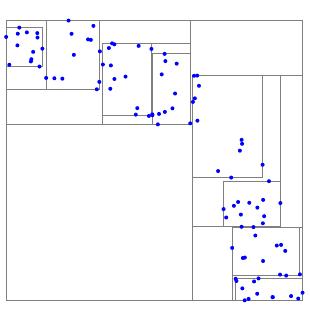
But how can we efficiently search through all the quads to find nearby quads? We organize our four-dimensional points into a $kd$-tree. We'll illustrate by organizing the following collection of two-dimensional points into a binary search tree.
Any set of points sits inside a bounding box, the smallest rectangle that contains the points and whose sides are parallel to the coordinate axes. The set of all points and their bounding box constitutes the root of the tree.
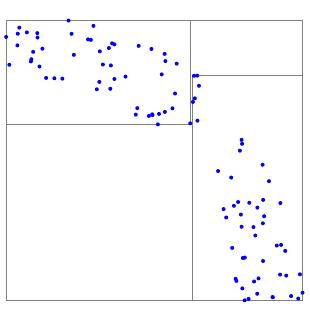
Next, we determine the dimension along which the points are most widely separated. In our example, the points are more spread out in the horizontal direction so we divide the points into two equal sets at the median of the horizontal coordinates. The points to the left and their bounding box form the left child of the root and the points to the right form the right child.
Now, continue subdividing until each point lies in a single node. The resulting tree structure is known as a $2d$-tree due to the two-dimensional nature of the point set.
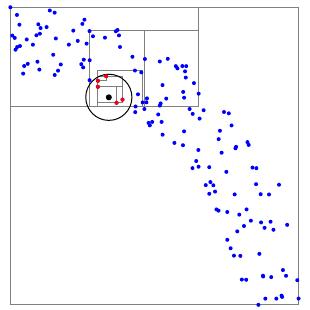
Suppose that we are presented with a new point $p$ and a distance $r$, and we'd like to find all the points in our original set that are within a distance $r$ of $p$.
Given a bounding box, we can compute the minimum distance from $p$ to the bounding box.
To begin the search, start with the root of the tree and ask whether the minimum distance from $p$ to the root's bounding box is less than $r$. If not, there are no points in the point set within a distance $r$ of $p$, and our search concludes. If the minimum distance is less than $r$, then we ask the same question of the two children and continue the search down the tree.
In this way, we eventually find all the points within a distance $r$ of $p$. In the example illustrated above, for instance, we have searched through 150 points by examining only 14 bounding boxes to find five points within the given distance.
This is an example of a $2d$-tree. Astronmetry.net constructs an index by organizing the quads present in the reference into a searchable $4d$-tree.
Verifying a match
Once we have identified a quad in our image, we search through the $4d$-tree for quads that are within a reasonable tolerance. Since the index does not contain every quad, it's possible we do not find any quads that match. However, there are plenty of quads in our image so we continue with another. Usually, there will be a large number of possible matches so we need to determine which is the best.
A quad in the index that is close to a quad in our image produces an "alignment" of the image onto the celestial sphere, as returned by my search.
With many nearby quads, how do we know which to accept? If a quad produces the correct alignment, we will have two lists of stars, one in the image and one in the reference, and a correspondence between them. Therefore, we search through a second $kd$-tree to find stars that are near to those in the reference quad and check to see if the corresponding stars are present in the image. Of course, even with the correct alignment, it's possible that stars do not appear in their expected location as they may be occluded by a planet, satellite, or comet or they may not be correctly identified as stars when the image is processed.
Due to the probabilistic nature of this question, the choice of whether to accept a proposed alignment is made using Bayesian decision theory. This enables Astrometry.net to set a high threshold for accepting a potential match, which eliminates most false positives. In tests, Astrometry.net is able to correctly recognize 99.9% of testing images with no false positives.
Summary
The central idea that leads to the impressive results achieved by Astrometry.net is the ability to identify certain features, quads, that can be expressed in a form that is easily searchable.
One can imagine other choices. For instance, using configurations of three stars, "tris," would allow us to represent features using 2-dimensional points. Our index would then squeeze all of our reference features into the unit square. Remember that noise in the images we are processing means that there is uncertainty in the coordinates of these features. Suppose, for instance, that we can only guarantee that a coordinate lies in an interval of width 0.1. The tri then lies somewhere in a square of area 0.01, which is 1% of the area of the unit square. We can detect at most 100 distinct tris.
Because quads live in 4-dimensional space, however, a quad would only occupy a volume of 0.0001 under these assumptions, which means we could distinguish 10,000 distinct quads.
Clearly, using a configuration of five stars would enable us to distinguish an even greater number of configurations. The trade-off, however, is that searching the $kd$-tree takes longer because we have more coordinates to work with. The choice to use quads is a compromise between the efficiency of the search and the number of nearby quads, and resulting proposed alignments, that need to be searched.
Astrometry.net, created by Dustin Lang, David Hogg, Keir Mierle, Michael Blanton, and Sam Roweis, enables a vast collection of images, including those made by amateur astronomers, to be used in astronomical research. What's presented here is a fairly broad overview that skims over many details of the implementation. Readers wanting to know more are encouraged to read the collaborators' paper or Lang's thesis, which presents a complete picture.
References


 David Austin
David Austin