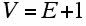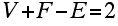Euler's Polyhedral Formula
Posted December 2004.
A theorem which would make both my list of 10 favorite theorems and my list of 10 most influential theorems . . .
Joe Malkevitch
York College (CUNY)
malkevitch at york.cuny.edu 
1. Introduction
It's coming to the end of the calendar year and a lot of people are producing lists. What were the 10 largest box-office blockbusters? What were the 10 best movies of the year? Who are the 10 best dressed men and 10 worst dressed women? One can also construct more grandiose lists. Who were the 10 best pitchers of all time or what were the 10 greatest movies? What appears on a list constructed by the same person can change dramatically with slight wording changes. Thus, the list of my 10 favorite movies might not coincide with my list of the 10 greatest movies ever made.
Does it make sense to construct lists related to mathematics? What about a list of the 10 greatest mathematicians? 10 greatest women mathematicians? The 10 most influential theorems? The 10 niftiest theorems?
On the one hand constructing lists is perhaps silly. How can one make a list of the 10 greatest composers of classical music? Must I leave Tchaikovsky out to include Mahler or Handel? Yet, from another perspective constructing lists of this kind makes one think about a wide variety of value-laden issues. What makes a composer great? Should a composer of a few great pieces be put on a short list of greats while another composer who perhaps composed nothing that rose to the heights of the first person, yet composed 100 times as many pieces at a very high level of inspiration, is omitted? This being the first of my last two columns as solo editor of the Feature Column, perhaps readers will indulge me if I write two columns about a theorem which would make both my list of 10 favorite theorems and my list of 10 most influential theorems. This theorem involves Euler's polyhedral formula (sometimes called Euler's formula).
Today we would state this result as: The number of vertices V, faces F, and edges E in a convex 3-dimensional polyhedron, satisfy V + F - E = 2. Aspects of this theorem illustrate many of the themes that I have tried to touch on in my columns.
2. Basic ideas
Polyhedra drew the attention of mathematicians and scientists even in ancient times. The Egyptians built pyramids and the Greeks studied "regular polyhedra," today sometimes referred to as the Platonic Solids . What is a polyhedron? This question is remarkably hard to answer simply! Part of the problem is that as scholars have studied "polyhedral" objects in greater detail, the idea of what is a "legal" polyhedron has changed and evolved. "Traditional polyhedra" consist of flat faces, straight edges, and vertices, but exactly what rules do these individual parts have to obey, and what additional global conditions should be imposed? Which of the following objects below should be allowed to qualify as polyhedra?
a. A cube with a triangular tunnel bored through it.
(Problem: The "faces" that lie in planes are not always polygons.)
b. The portion of the surface of three pairwise intersecting vertical planes (e.g. "triangular cylinder").
(Problem: This surface does not have any vertices.)
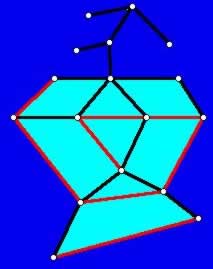
c. The surface formed based on three rays which meet at a point as shown below.
(Problem: The "faces" are not polygons but unbounded portions of planes.)
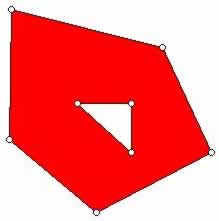
Almost certainly, in the early days of the study of polyhedra, the word referred to convex polyhedra. A set is convex if the line segment joining any two points in the set is also in the set. Among the nice properties of convex sets is the fact that the set of points in common to a collection of convex sets is convex. Loosely speaking, non-convex sets in two dimensions have either notches or holes. The diagram below shows a non-convex polygon and a convex polygon.
The planar set below is not convex, but note that it does not satisfy the usual definition of a polygon, even through it is bounded by sections of straight lines.
The faces of a convex polyhedron consist of convex polygons. However, this approach to defining polyhedra rules out a "polyhedron" which goes off to infinity, such as the surface below:

This polyhedron has three rays (which, if extended, should meet at a point) and three line segments as edges of the polyhedron, rather than having edges which are line segments. One can also have examples where there are only rays (see earlier diagram).
Traditionally, what is essential for a polyhedron is that it consist of pieces of flat surfaces, but as time has gone on, the definition of "legal" polyhedra has been broadened. Typically this has resulted in a dramatic improvement in the insights that have been obtained concerning the original "narrower" class of polyhedra and the newer class of polyhedra under the broader definition.
For example, in Euclid's Elements there is a "proof" that there are 5 regular polyhedra, based on the implicit assumption that the faces of the polyhedra are convex polygons. A regular polyhedron is one in which all faces are congruent regular (convex) polygons and all vertices are "alike." This means that there are the same number of regular polygons at every vertex. Using this definition one finds there are 5 regular polyhedra.
If one has a supply of regular pentagonal polygons such as the one below,
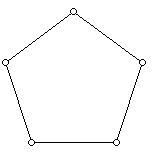
one can assemble 12 of them, three at each vertex, to form the solid known as the regular dodecahedron.
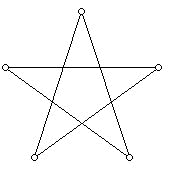
However, the Greeks knew about the polygon that today is called the pentagram:
This polygon has a good claim to be called a regular polygon because all its sides have equal length and the angle between two consecutive sides of the polygon is always the same. However, this polygon, when drawn in the plane, does not define a convex set and the sides of the polygon intersect each other. Nonetheless, when mathematicians considered the idea of "non-convex" regular polyhedra where such "star polygons" were permitted, they discovered some new examples of "regular polyhedra," now known as the Kepler-Poinsot polyhedra . Later H.S.M. Coxeter and Branko Grünbaum broadened the rules for polyhedra and discovered other "regular polyhedra."
The systematic study of polyhedra began relatively early in the history of mathematics as shown by the place they hold in Euclid's Elements . Yet it remained until the 18th century before there was a statement of the result that
3. Euler's contribution
 It appears that Leonard Euler (1707-1783) was the first person to notice the fact that for convex 3-dimensional polyhedra V + F - E = 2.
It appears that Leonard Euler (1707-1783) was the first person to notice the fact that for convex 3-dimensional polyhedra V + F - E = 2.
Euler mentioned his result in a letter to Christian Goldbach (of Goldbach's Conjecture fame) in 1750. He later published two papers in which he described what he had done in more detail and attempted to give a proof of his new discovery.
It is sometimes claimed that Descartes (1596-1650) discovered Euler's polyhedral formula earlier than Euler. Though Descartes did discover facts about 3-dimensional polyhedra that would have enabled him to deduce Euler's formula, he did not take this extra step. With hindsight it is often difficult to see how a talented mathematician of an earlier era did not make a step forward that with today's insights seems natural, however, it often happens. If one is wandering through a maze of tunnels in a cave, perhaps one comes across a large hall of impressive formations with many tunnels. You may explore some of these without successfully discovering any impressive new formations and go back home contented. However, it might have turned out that one of the many tunnels you did not have time to explore would have led you to an even more spectacular chamber. Descartes' Theorem is a very lovely result in its own right, and in 3 dimensions it is equivalent to Euler's polyhedral formula.
It is tempting to speculate about why all the able mathematicians, artists, and scholars who investigated polyhedra in the years before Euler did not notice the polyhedral formula. There certainly are results in Euclid's Elements and in the work of later Greek geometers that appear more complex than Euler's  polyhedral formula. Presumably a major factor, in addition to the lack of attention paid to counting problems in general up to relatively recent times, was that people who thought about polyhedra did not see them as structures with vertices, edges, and faces. It appears that Euler did not view them this way either! He seems to have adopted a fairly conventional view of polyhedra. In his view the "vertex" of a polyhedron is a solid angle or a part of a "polyhedral cone" that starts at the vertex. Given that today Euler is credited with being the "father" of graph theory for having solved the Königsberg bridge problem using graph theory ideas, one might have expected him to see the graph associated with a polyhedron. However, he does not appear to have thought of polyhedra as graphs, a step not exploited until rather later by Cauchy (1789-1856).
polyhedral formula. Presumably a major factor, in addition to the lack of attention paid to counting problems in general up to relatively recent times, was that people who thought about polyhedra did not see them as structures with vertices, edges, and faces. It appears that Euler did not view them this way either! He seems to have adopted a fairly conventional view of polyhedra. In his view the "vertex" of a polyhedron is a solid angle or a part of a "polyhedral cone" that starts at the vertex. Given that today Euler is credited with being the "father" of graph theory for having solved the Königsberg bridge problem using graph theory ideas, one might have expected him to see the graph associated with a polyhedron. However, he does not appear to have thought of polyhedra as graphs, a step not exploited until rather later by Cauchy (1789-1856).
Because he did not look at the polyhedra he was studying as graphs, Euler attempted to give a proof of the formula based on decomposing a polyhedron into simpler pieces. This attempt does not meet modern standards for a proof. His argument was not correct. However, results proven later make it possible to use Euler's technique to prove the polyhedral formula.
Although Euler did not give the first correct proof of his formula, one can not prove conjectures that have not been made. It appears to have been the French mathematician Adrian Marie Legendre (1752-1833) who gave the first proof, though he did not use combinatorial methods. Ironically, this quintessentially combinatorial theorem was given a metric proof by Legendre. Despite using metrical methods the proof is very insightful and clever.
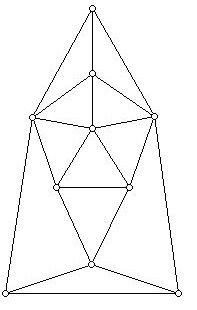
While Euler first formulated the polyhedral formula as a theorem about polyhedra, today it is often treated in the more general context of connected graphs (e.g. structures consisting of dots and line segments joining them that are in one piece). Cauchy seems to have been the first person to make this important connection. He in essence noticed that the graph of a convex polyhedron (or more generally what today we would call a polyhedron which is topologically homeomorphic to a sphere) has a planar connected graph. A plane graph is one which has been drawn in the plane in such a way that the edges meet (intersect) only at a vertex. A graph which has the potential to be drawn in this way is known as a planar graph. A typical plane graph is shown in the diagram below. The number of edges at a vertex in such a connected graph (e.g. one piece) is called the degree or valence of the vertex. For example, in the diagram below the vertices on the vertical mirror line of the drawing have valence 3, 4, 5, 4, from top to bottom. Do you think there is some convex 3-dimensional polyhedron whose graph is isomorphic to this graph? (You will be able to answer this question using Steinitz's Theorem, which will be treated in the continuation of this column next month.)
An intuitive way to see that convex polyhedra give rise to plane graphs (it's the converse that is the difficult part of Steinitz's Theorem) follows. Cut out one of the polyhedron's faces along the edges that bound the face, and transform the remaining faces into stretchable rubber. Now stretch the polyhedron with one face removed to lay it flat in the plane so that the removed face becomes the unbounded region associated with the resulting plane graph.
To help you understand this process look at the box-like polyhedron below, which from a combinatorial point of view is a "cube." The lines which are red are those edges of the box which are "hidden" when the box is viewed from the front.
In the diagram below we have highlighted in turquoise the face of the polyhedron that we remove from this box, and now pretend that the remaining structure is made of rubber.
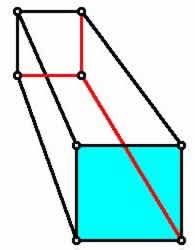
Figure 1
We now stretch and flatten out the remaining surface so that the turquoise face becomes the unbounded region of the resulting graph that can be drawn in the plane (see Figure 2 below). The position of the red edges is shown to help you visualize what is happening. Of course the turquoise region should be shown as going off to "infinity," even though it appears only as a bounded face in the original polyhedron. The back face of the box is now shown as having a vertical and horizontal red edge. The plane that contains this back face can be thought of as the plane into which we stretch and flatten out the surface of the box with the turquoise face removed. It's fairly clear that the faces of the original polyhedron are preserved by this process. It is also clear where these faces appear in the plane graph representation of the polyhedron, except perhaps for the turquoise face in Figure 1. It is common for people to forget to count this face when they are counting the faces of a graph drawn in the plane. Plane graphs always have at least one face, the "infinite face."
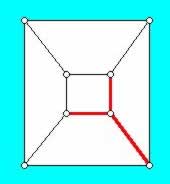
Figure 2
Although there are other ways of seeing that the graphs of convex 3-dimensional polyhedra or graphs on the sphere have planar graphs (i.e. at some stage use stereographic projection), this argument hopefully makes clear that the graphs that can be drawn on a sphere (polyhedra whose graphs are homeomorphic to a sphere) where edges meet only at vertices are the same as the graphs that can be drawn in a plane where edges cross only at vertices.
4. Proofs of the polyhedral formula
There are many proofs of the Euler polyhedral formula, and, perhaps, one indication of the importance of the result is that David Eppstein has been able to collect 17 different proofs . In a sense the most straightforward proofs are ones using mathematical induction. One can prove the result by doing induction on either the number of edges, faces or vertices of the graph.
The following proof is especially attractive. It follows the development given by H. Rademacher and O. Toeplitz based on an approach of Von Staudt (1798-1867). Suppose that G is a connected graph that has been embedded in the plane. Think of the infinite face of the graph as being the ocean, the edges of the graphs being dikes made of earth, and the faces of the graph other than the infinite face as being dry fields. A typical example of such a connected plane graph is shown below.

The blue in this diagram does not go off to infinity but you should think of it as doing that. In the diagram below an edge of one circuit in the graph which bounds a face is shown in red, and this edge is adjacent to the ocean. When the dike represented by this red edge is "breached," the field on the other side of the dike is opened up to the ocean and becomes flooded, as indicated by the turquoise (for illustrative purposes - the color of the water really should be the same as the ocean!).
If a connected graph has circuits that bound faces, one can eliminate one edge from each of these circuits in a way that preserves the property that the graph remains connected. There is a one-to-one correspondence between the edges removed to get to a connected graph without circuits (because of the Jordan curve theorem) and the faces of the graph which are not the infinite face. The edges necessary to do this are shown in red below, and the fact that the fields flood is shown in turquoise.
The resulting graph of black edges forms a spanning tree of the original graph. A spanning tree of a connected graph is a subgraph which is a tree (e.g. a graph which is connected and has no circuit) and includes all the vertices of the original graph. Thus, a spanning tree of a connected graph has the same number of vertices as the original graph, but fewer edges (unless the original graph is a tree). Note that for any tree, we have:
Now, let us count the edges of the original graph by adding the number of edges removed to get a tree, the red edges above, to the number of black edges above. Thus,
Now, we know that ERED is equal to one less than the number of faces of the original graph. This is true because we needed one red edge to flood each dry field (e.g. the non-infinite faces), and the graph had one more face, the infinite face. The number of EBLACK edges is given by one less than the number of vertices in the graph, because the black edges are a spanning tree of the original graph. Hence we have:
Rearranging the terms in this equation gives:
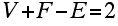
Euler's formula does not hold for any graph embedded on a surface. It holds for graphs embedded so that edges meet only at vertices on a sphere (or in the plane), but not for graphs embedded on the torus, a one-holed donut. The fundamental theorem that is used directly or indirectly in a proof of the Euler polyhedra formula for graphs depends on the Jordan Curve theorem , which states that any simple closed curve divides the plane into three sets, those points on the curve, those inside the curve, and those outside the curve.
As interest in Euler's polyhedral formula evolved in the 19th century, many attempts were made to generalize the formula. This research laid the foundation for the development of topology and algebraic topology and for a theory of surfaces. It was soon discovered that some surfaces could be "oriented" in a consistent way only locally but not globally. The famous Möbius (1790-1868) Band serves as an illustration of a surface of this kind. (This surface was independently discovered somewhat earlier by Johann Listing (1808-1882).) This research led to a classification of "orientable surfaces" in terms of what is known as the Euler Characteristic . This concept involves the notion of the genus of a graph: the smallest number of handles g that must be added to the surface of a sphere so that a graph can be embedded on the augmented surface in such a way that edges meet only at vertices. It turns out that every orientable surface in Euclidean space can be thought of as a sphere with a certain number of handles. To construct a handle on a sphere so as to eliminate an edge crossing for a graph on the surface, one can cut out two circles from the surface and join these circles by a cylindrical tube, the handle, as shown below.
If two edges in a graph drawn on a surface cross, one can eliminate the crossing by having one of the edges go over a small handle to avoid the crossing. It turns out that if a graph can be embedded without edges meeting anywhere other than at vertices on a surface with g handles, but on no surface with a smaller number of handles, then:

Since the sphere has no handles, g = 0 for the sphere, and the formula above reduces to Euler's formula. The connection between Euler's polyhedral formula and the mathematics that led to a theory of surfaces, both the orientable and unorientable surfaces, is still being pursued to this day. In addition, motivated by many problems involving the design of computer chips (integrated circuits), there has been an explosion of research about crossing number problems for graphs in the plane. This involves finding the minimum number of crossings when an abstractly defined graph is drawn in the plane. It turns out that the crossing number depends on whether or not the edges are allowed to be straight or curved. Many of these questions involve the use of Euler's formula to get estimates for the smallest number of crossings. Furthermore, Euler's formula is intimately connected with coloring problems of the faces of a graph. These coloring problems include not only the famous 4-color conjecture but also problems about coloring the faces of graphs on surfaces such as spheres with many handles.
Next month, I will continue my discussion of Euler's formula and point out some of the many lovely results that it has led to.
Joseph Malkevitch
York College (CUNY)
malkevitch at york.cuny.edu 
5. References
Aigner, M. and G. Ziegler, Proofs from the Book, 3rd. edition, Springer-Verlag.
Appel, K. ; Haken, W. Every planar map is four colorable. Bull. Amer. Math. Soc. 82 (1976), no. 5, 711--712. MR0424602 (54 #12561)
Barnette, David . Trees in polyhedral graphs. Canad. J. Math. 18 1966 731--736. MR0195753 (33 #3951)
Barnette, David . $W\sb{v}$ paths on 3-polytopes. J. Combinatorial Theory 7 1969 62--70. MR0248636 (40 #1887)
Barnette, David . On $p$-vectors of $3$-polytopes. J. Combinatorial Theory 7 1969 99--103. MR0244851 (39 #6165)
Barnette, David W. Projections of 3-polytopes. Israel J. Math. 8 1970 304--308. MR0262923 (41 #7528)
Barnette, David . Map coloring, polyhedra, and the four-color problem. The Dolciani Mathematical Expositions, 8. Mathematical Association of America, Washington, DC, 1983. x+168 pp. ISBN: 0-88385-309-4 MR0741465 (85e:05001).
Barnette, David W. ; Grünbaum, Branko . On Steinitz's theorem concerning convex $3$-polytopes and on some properties of planar graphs. 1969 The Many Facets of Graph Theory (Proc. Conf., Western Mich. Univ., Kalamazoo, Mich., 1968) pp. 27--40 Springer, Berlin MR0250916 (40 #4148)
Barnette, David ; Grünbaum, Branko . Preassigning the shape of a face. Pacific J. Math. 32 1970 299--306. MR0259744 (41 #4377)
Beck, Anatole ; Bleicher, Michael N. ; Crowe, Donald W. Excursions into mathematics. The millennium edition. With a foreword by Martin Gardner. A K Peters, Ltd., Natick, MA, 2000. xxvi+499 pp. ISBN: 1-56881-115-2 MR1744676 (2000k:00002)
Graph connections. Relationships between graph theory and other areas of mathematics. Edited by Lowell W. Beineke and Robin J. Wilson. Oxford Lecture Series in Mathematics and its Applications, 5. The Clarendon Press, Oxford University Press, New York, 1997. xii+291 pp. ISBN: 0-19-851497-2 MR1634542 (99a:05001)
Biggs, Norman L. ; Lloyd, E. Keith ; Wilson, Robin J. Graph theory. 1736--1936. Second edition. The Clarendon Press, Oxford University Press, New York, 1986. xii+239 pp. ISBN: 0-19-853916-9 MR0879117 (88e:01035)
Bruggesser, H. ; Mani, P. Shellable decompositions of cells and spheres. Math. Scand. 29 (1971), 197--205 (1972). MR0328944 (48 #7286)
Cauchy, A., Recherches sur les Polyèdres - Premier Mémoire, Journal de l'École Polytechnique, 9 (Cahier 16) (1813) 68-86.
Dress, Andreas W. M. A combinatorial theory of Grünbaum's new regular polyhedra. II. Complete enumeration. Aequationes Math. 29 (1985), no. 2-3, 222--243. MR0819312 (87e:51028)
Eberhard, V., Zur Morphologie der Polyeder, Leipzig, 1891.
Euler, L., Elementa doctrinae solidorum, Novi Comm. Acad. Sci. Imp. Petropol., 4 (1752-3) 109-140 (published 1758), Opera Omnia (1) Volume 26, 72-93.
Euler, L., Demonstratio nonnullarum insignium proprietatum quibas solida hedris planis inclusa sunt praedita, Novi Comm. Acad. Sci. Imp. Petropol., 4 (1752-1753), 140-160 (published 1758) Opera Omnia (1) Volume 26, 94-108.
Fáry, István . On straight line representation of planar graphs. Acta Univ. Szeged. Sect. Sci. Math. 11, (1948). 229--233. MR0026311 (10,136f)
Möbius and his band. Mathematics and astronomy in nineteenth-century Germany. Edited by John Fauvel, Raymond Flood and Robin Wilson. The Clarendon Press, Oxford University Press, New York, 1993. vi+172 pp. ISBN: 0-19-853969-X MR1249066 (94m:01023)
Federico, Pasquale Joseph . Descartes on polyhedra. A study of the De solidorum elementis . Sources in the History of Mathematics and Physical Sciences, 4. Springer-Verlag, New York-Berlin, 1982. viii+145 pp. ISBN: 0-387-90760-2 MR0680214 (84c:01024)
Felsner, Stefan . Convex drawings of planar graphs and the order dimension of 3-polytopes. Order 18 (2001), no. 1, 19--37. MR1844514 (2002f:05061)
Fisher, J. C. An existence theorem for simple convex polyhedra. Discrete Math. 7 (1974), 75--97. MR0333984 (48 #12303)
Fisher, J. C. Five-valent convex polyhedra with prescribed faces. J. Combinatorial Theory Ser. A 18 (1975), 1--11. MR0365360 (51 #1612)
Handbook of discrete and computational geometry. Second edition. Edited by Jacob E. Goodman and Joseph O'Rourke. Discrete Mathematics and its Applications (Boca Raton). Chapman & Hall/CRC, Boca Raton, FL, 2004. xviii+1539 pp. ISBN: 1-58488-301-4 MR2082993
Grünbaum, B. Some analogues of Eberhard's theorem on convex polytopes. Israel J. Math. 6 1968 398--411 (1969). MR0244854 (39 #6168)
Grünbaum, Branko . Planar maps with prescribed types of vertices and faces. Mathematika 16 1969 28--36. MR0245460 (39 #6768)
Grünbaum, Branko . Polytopes, graphs, and complexes. Bull. Amer. Math. Soc. 76 1970 1131--1201. MR0266050 (42 #959)
Grünbaum, Branko . Polytopal graphs. Studies in graph theory, Part II, pp. 201--224. Studies in Math., Vol. 12, Math. Assoc. Amer., Washington, D. C., 1975. MR0406868 (53 #10654)
Grünbaum, Branko . Regular polyhedra---old and new. Aequationes Math. 16 (1977), no. 1-2, 1--20. MR0467497 (57 #7353)
Grünbaum, Branko . A convex polyhedron which is not equifacettable. Geombinatorics 10 (2001), no. 4, 165--171. MR1825338
Grünbaum, B., Convex Polytopes, 2nd. edition, Springer-Verlag, New York, 2003 (first edition, 1967, Wiley-Interscience).
Grünbaum, B. ; Johnson, N. W. The faces of a regular-faced polyhedron. J. London Math. Soc. 40 1965 577--586. MR0181935 (31 #6161)
Grünbaum, Branko ; Malkevitch, Joseph . Pairs of edge-disjoint Hamiltonian circuits. Aequationes Math. 14 (1976), no. 1/2, 191--196. MR0414443 (54 #2544b)
Grünbaum, B. ; Motzkin, T. S. Longest simple paths in polyhedral graphs. J. London Math. Soc. 37 1962 152--160. MR0139161 (25 #2598)
Grünbaum, Branko ; Motzkin, Theodore S. On polyhedral graphs. 1963 Proc. Sympos. Pure Math., Vol. VII pp. 285--290 Amer. Math. Soc., Providence, R.I. MR0153005 (27 #2976)
Grünbaum, B. ; Motzkin, T. S. The number of hexagons and the simplicity of geodesics on certain polyhedra. Canad. J. Math. 15 1963 744--751. MR0154182 (27 #4133)
Grünbaum, Branko ; Shephard, G. C. Tilings and patterns. W. H. Freeman and Company, New York, 1987. xii+700 pp. ISBN: 0-7167-1193-1 MR0857454 (88k:52018)
Grünbaum, Branko ; Zaks, Joseph . The existence of certain planar maps. Discrete Math. 10 (1974), 93--115. MR0349455 (50 #1949)
Haussner, R., Abhandlungen über die regelmäßigen Sternkörper, Ostwald's Klassiker de Exakten Wissenschaften, Nr. 151, Wilhelm Engelmann, Leipzig, 1906.
Hilton, Peter ; Pedersen, Jean . Descartes, Euler, Poincaré, Pólya---and polyhedra. Enseign. Math. (2) 27 (1981), no. 3-4, 327--343 (1982). MR0659155 (83g:52008)
Jendrol', Stanislav . A new proof of Eberhard's theorem. Acta Fac. Rerum Natur. Univ. Comenian. Math. 31 (1975), 1--9. MR0385718 (52 #6577)
Jendro\soft l, Stanislav . On the face-vectors of trivalent convex polyhedra. Math. Slovaca 33 (1983), no. 2, 165--180. MR0699086 (85f:52018)
Jendro\soft l, Stanislav . On face vectors and vertex vectors of convex polyhedra. Discrete Math. 118 (1993), no. 1-3, 119--144. MR1230057 (94h:52017)
Johnson, Norman W. Convex polyhedra with regular faces. Canad. J. Math. 18 1966 169--200. MR0185507 (32 #2973)
Jucovi\v c, Ernest . On the number of hexagons in a map. J. Combinatorial Theory Ser. B 10 1971 232--236. MR0278179 (43 #3910)
Jucovi\v c, E. On the face vector of a $4$-valent $3$-polytope. Studia Sci. Math. Hungar. 8 (1973), 53--57. MR0333985 (48 #12304)
Kalai, Gil . A simple way to tell a simple polytope from its graph. J. Combin. Theory Ser. A 49 (1988), no. 2, 381--383. MR0964396 (89m:52006)
Polytopes---combinatorics and computation. Including papers from the DMV-Seminar "Polytopes and Optimization" held in Oberwolfach, November 1997. Edited by Gil Kalai and Günter M. Ziegler. DMV Seminar, 29. Birkhäuser Verlag, Basel, 2000. vi+225 pp. ISBN: 3-7643-6351-7 MR1785290 (2001d:52002)
Klee, Victor . The Euler characteristic in combinatorial geometry. Amer. Math. Monthly 70 1963 119--127. MR0146101 (26 #3627)
Lakatos, Imre . Proofs and refutations. The logic of mathematical discovery. Edited by John Worrall and Elie Zahar. Cambridge University Press, Cambridge-New York-Melbourne, 1976. xii+174 pp. MR0479916 (58 #122)
Legendre, A., Élements de géometrie, Firmin Didot, Paris, 1794.
Lebesgue, H., Remarques sur les deux premières demonstrations du théorèm d'Euler, rélatif aux polyèdres, Bulletin de la Socièté Mathématique de France, 52 (1924) 315-336.
Lebesgue, Henri . Quelques conséquences simples de la formule d'Euler. (French) J. Math. Pures Appl. 19, (1940). 27--43. MR0001903 (1,316i)
L'Huilier, S., Démonstration immédiate d'un théorème est susceptible, Mém. Acad. Imp. Sci. St. Pétersb., 4 (1811) 271-301.
L'Huilier, S., Mémoire sur la Polyédrométrie, Annales de Mathématiques, 3 (1812-1813) 169-189.
Malkevitch, Joseph . Properties of planar graphs with uniform vertex and face structure. Memoirs of the American Mathematical Society, No. 99 American Mathematical Society, Providence, R.I. 1970 iv+116 pp. MR0260616 (41 #5240)
Malkevitch, Joseph . The first proof of Euler's formula. Mitt. Math. Sem. Giessen No. 165, (1984), 77--82. MR0745872 (86b:01015)
Malkevitch, Joseph . Polytopal graphs. Selected topics in graph theory, 3, 169--188, Academic Press, San Diego, CA, 1988. MR1205401
McMullen, Peter . On simple polytopes. Invent. Math. 113 (1993), no. 2, 419--444. MR1228132 (94d:52015)
McMullen, Peter ; Schulte, Egon . Abstract regular polytopes. Encyclopedia of Mathematics and its Applications, 92. Cambridge University Press, Cambridge, 2002. xiv+551 pp. ISBN: 0-521-81496-0 MR1965665 (2004a:52020)
McMullen, P. ; Shephard, G. C. Convex polytopes and the upper bound conjecture. Prepared in collaboration with J. E. Reeve and A. A. Ball. London Mathematical Society Lecture Note Series, 3. Cambridge University Press, London-New York, 1971. iv+184 pp. MR0301635 (46 #791)
Mohar, Bojan ; Thomassen, Carsten . Graphs on surfaces. Johns Hopkins Studies in the Mathematical Sciences. Johns Hopkins University Press, Baltimore, MD, 2001. xii+291 pp. ISBN: 0-8018-6689-8 MR1844449 (2002e:05050)
Motzkin, Theodore S. The evenness of the number of edges of a convex polyhedron. Proc. Nat. Acad. Sci. U.S.A. 52 1964 44--45. MR0173198 (30 #3411)
Robertson, Neil ; Sanders, Daniel ; Seymour, Paul ; Thomas, Robin . The four-colour theorem. J. Combin. Theory Ser. B 70 (1997), no. 1, 2--44. MR1441258 (98c:05065)
Poinsot, L., Sur les polygones and les polyèdres, J. École Polytech., 4 (cahier 10) (1810) 16-48.
Rademacher, Hans ; Toeplitz, Otto . The enjoyment of math. Translated from the second (1933) German edition and with additional chapters by H. Zuckerman. Princeton Science Library. Princeton University Press, Princeton, NJ, 1994. iv+205 pp. ISBN: 0-691-02351-4 MR1300411 (95h:00002)
Read, Ronald C. ; Wilson, Robin J. An atlas of graphs. Oxford Science Publications. The Clarendon Press, Oxford University Press, New York, 1998. xii+454 pp. ISBN: 0-19-853289-X MR1692656 (2000a:05001)
Shaping space. A polyhedral approach. Proceedings of the conference held in Northampton, Massachusetts, April 6--8, 1984. Edited by Marjorie Senechal and George Fleck. Design Science Collection. A Pro Scientia Viva Title. Birkhäuser Boston, Inc., Boston, MA, 1988. xx+284 pp. ISBN: 0-8176-3351-0 MR0937069 (89b:52016)
Shephard, G. C. Combinatorial properties of associated zonotopes. Canad. J. Math. 26 (1974), 302--321. MR0362054 (50 #14496)
Shephard, G. C. Convex polytopes with convex nets. Math. Proc. Cambridge Philos. Soc. 78 (1975), no. 3, 389--403. MR0390915 (52 #11738)
Steinitz, E., Über die Eulerschen Polyederrelationen, Archiv. für Mathematik und Physik, 11 (1906) 86-88.
Steinitz, Ernst ; Rademacher, Hans . Vorlesungen über die Theorie der Polyeder unter Einschluss der Elemente der Topologie. Reprint der 1934 Auflage. Grundlehren der Mathematischen Wissenschaften, No. 41. Springer-Verlag, Berlin-New York, 1976. viii+351 pp. MR0430958 (55 #3962)
Thomassen, Carsten . Planarity and duality of finite and infinite graphs. J. Combin. Theory Ser. B 29 (1980), no. 2, 244--271. MR0586436 (81j:05056) .
Thomassen, Carsten . Kuratowski's theorem. J. Graph Theory 5 (1981), no. 3, 225--241. MR0625064 (83d:05039)
Thomassen, C. Plane representations of graphs. Progress in graph theory (Waterloo, Ont., 1982), 43--69, Academic Press, Toronto, ON, 1984. MR0776790 (86g:05032)
Thomassen, Carsten . A refinement of Kuratowski's theorem. J. Combin. Theory Ser. B 37 (1984), no. 3, 245--253. MR0769367 (86e:05059)
Thomassen, Carsten . Rectilinear drawings of graphs. J. Graph Theory 12 (1988), no. 3, 335--341. MR0956195 (89i:05111)
Thomassen, Carsten . The graph genus problem is NP-complete. J. Algorithms 10 (1989), no. 4, 568--576. MR1022112 (91d:68054)
Thomassen, Carsten . A link between the Jordan curve theorem and the Kuratowski planarity criterion. Amer. Math. Monthly 97 (1990), no. 3, 216--218. MR1048433 (91g:55005)
Thomassen, Carsten . Every planar graph is $5$-choosable. J. Combin. Theory Ser. B 62 (1994), no. 1, 180--181. MR1290638 (95f:05045)
Thomassen, Carsten . Trees in triangulations. J. Combin. Theory Ser. B 60 (1994), no. 1, 56--62. MR1256583 (95e:05039)
Thomassen, Carsten . $3$-list-coloring planar graphs of girth $5$. J. Combin. Theory Ser. B 64 (1995), no. 1, 101--107. MR1328294 (96c:05070)
Tutte, W. T. Convex representations of graphs. Proc. London Math. Soc. (3) 10 1960 304--320. MR0114774 (22 #5593)
Von Staudt, G., Geometrie der Lage, Nürenberg, 1847.
West, Douglas B. Introduction to graph theory. Prentice Hall, Inc., Upper Saddle River, NJ, 1996. xvi+512 pp. ISBN: 0-13-227828-6 MR1367739 (96i:05001)
Wilson, Robert A. Graphs, colourings and the four-colour theorem. Oxford University Press, Oxford, 2002. viii+141 pp. ISBN: 0-19-851061-6 MR1888337 (2003c:05095)
Zaks, Joseph . Non-Hamiltonian simple planar graphs. Theory and practice of combinatorics, 255--263, North-Holland Math. Stud., 60, North-Holland, Amsterdam, 1982. MR0806988 (86j:05095)
Ziegler, Günter M. Lectures on polytopes. Graduate Texts in Mathematics, 152. Springer-Verlag, New York, 1995. x+370 pp. ISBN: 0-387-94365-X MR1311028 (96a:52011)
Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet can be used to get additional bibliographic information and reviews of some these materials. Some of the items above can be accessed via the ACM Portal , which also provides bibliographic services.










 It appears that Leonard Euler (1707-1783) was the first person to notice the fact that for convex 3-dimensional polyhedra V + F - E = 2.
It appears that Leonard Euler (1707-1783) was the first person to notice the fact that for convex 3-dimensional polyhedra V + F - E = 2. polyhedral formula. Presumably a major factor, in addition to the lack of attention paid to counting problems in general up to relatively recent times, was that people who thought about polyhedra did not see them as structures with vertices, edges, and faces. It appears that Euler did not view them this way either! He seems to have adopted a fairly conventional view of polyhedra. In his view the "vertex" of a polyhedron is a solid angle or a part of a "polyhedral cone" that starts at the vertex. Given that today Euler is credited with being the "father" of graph theory for having solved the Königsberg bridge problem using graph theory ideas, one might have expected him to see the graph associated with a polyhedron. However, he does not appear to have thought of polyhedra as graphs, a step not exploited until rather later by
polyhedral formula. Presumably a major factor, in addition to the lack of attention paid to counting problems in general up to relatively recent times, was that people who thought about polyhedra did not see them as structures with vertices, edges, and faces. It appears that Euler did not view them this way either! He seems to have adopted a fairly conventional view of polyhedra. In his view the "vertex" of a polyhedron is a solid angle or a part of a "polyhedral cone" that starts at the vertex. Given that today Euler is credited with being the "father" of graph theory for having solved the Königsberg bridge problem using graph theory ideas, one might have expected him to see the graph associated with a polyhedron. However, he does not appear to have thought of polyhedra as graphs, a step not exploited until rather later by