The bottom in each figure also shows a kind of dead zone in which no triangles are evident. This zone shrinks as the number of subdivisions increases. I do not know that anyone has remarked on this, but it ought not to be difficult to explain, and rather precisely.
The drift to the south
Let's look again at the apparent flow downwards in successive subdivisions. The images above don't show this very well, because the points recording subdivision triangles achieve saturation. But there are other ways to make it more apparent. The following figure is almost the same as one we have seen previously, but now the bar graph on the right side records the proportion in corresponding horizontal slices.
There ought to be no need to reproduce the point plots, so the following figures just exhibit the bar graphs:
These should make it much clearer that as the number of subdivisions increases, there is a flow towards the bottom. The impression is reinforced by the following table showing the means of the distributions: $$ \eqalignno { \hbox{Number of subdivisions:} & & \; 0 & \quad 1 & \quad 2 & \quad 3 & \quad 4 & \quad 5 & \quad 6 & \quad 7 &\quad 8 & \quad 9 & \quad 10 \cr \hbox{Mean height:} & & 0.5 & 0.3683 & 0.3136 & 0.2656 & 0.2296 & 0.2013 & 0.1781 & 0.1588 & 0.1425 & 0.1285 & 0.1163 \cr } $$
These form an approximate geometric sequence with ratio $q \sim 0.906 = e^{-0.099}$.
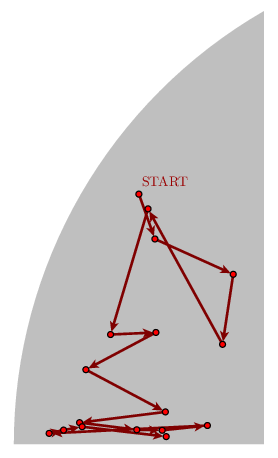
This flow, at least, is partly understood, although in terms we haven't yet seen. Corresponding to the barycentric subdivision of triangles is a kind of random walk among the shapes of triangles. Start with a triangle $T_{0}$, and suppose $S_{1}$, ... , $S_{6}$ are the triangles you get by subdividing it. Toss a die. If the face marked $i$ appears, let $T_{1} = S_{i}$. If we do this repeatedly, we get a sequence of triangles $T_{m}$ in which $T_{m+1}$ is a random choice among the subdivisions of $T_{m}$. If I plot for each the corresponding point of the region $\Sigma$, I get a path in $\Sigma$. Here, for example, is what I get if I start with the same triangle $T_{0}$ whose vertices are $(0,0)$, $(1,0)$, $(1/4, 1/2)$:
There are occasional bounces up, but the trend is towards the bottom. This is the way things usually go, as has also been proved rigorously by Barany et al.:
Theorem. (Barany et al.) A random walk among successive barycentric subdivisions of a triangle will almost certainly converge to flat triangles.
Empirically, one sees that as subdivision proceeds the shapes pile up along the bottom of $\Sigma$. This observation can be made more precise. Barycentric subdivision can be applied even to flat triangles, and produces other flat triangles. In order to understand the shapes that barycentric subdivision generates it is important to understand how it works for flat triangles.
There are therefore two reasons flat triangles are important. One is that under barycentric subdivision, triangles that are nearly flat behave approximately as if they were flat, and in particular all the triangles they divide into are also fairly flat. Another is that arbitrary triangles tend to become flatter and flatter after many subdivisions.
Consistently with the last theorem, the amount a child can bounce above its parent is rather limited. I have already mentioned that if a triangle is nearly flat, its children are also nearly flat. Given this, one might wonder if the triangles you see eventually converge to a fixed flat triangle. This is not, however, what you'd guess from the figure. In fact, what happens is the opposite: as the shapes become flatter and flatter, they traverse somewhat randomly in a horizontal direction. This has been discussed in some detail in the work of Diaconis and Miclo. Not only does barycentric subdivision make sense for flat triangles, but---as we shall see in a later section---it is simpler to understand than for non-degenerate triangles. In addition, Diaconis and Miclo prove that triangles that are nearly flat behave much like flat ones.
The barycentric subdivision of flat triangles is all by itself an interesting business, and quite different from what we have seen so far. The basic fact is that subdivision of a flat triangle produces more flat triangles. So we can apply to it much the same process that we did to real triangles. We start with some initial value of $x$, then compute successively all children of current values of $x$.
One could illustrate this as I illustrated the barycentric subdivisions of a given starting flat triangle. But this would not be so illuminating, since the interval $[0,1/2]$ simply fills up rapidly. There is no flow, but instead a gradual saturation. This is a proven fact: as time goes on, what we see is that the distribution of descendants approximates better and better a fixed density. (The technical way to phrase this is to say that the process is ergodic.) This also has been proved by Diaconis and Miclo, who prove in addition a few more properties of this density. In the following figure, one sees the approximate density after many subdivisions.
It seems to be at least continuous, although this has not been verified rigourously. How smooth is it?
Comments?
More about flat triangles
I have said that the analysis of Diaconis and Micro is based upon a close examination of what happens in the subdivision of flat triangles. This is relatively simple from both a theoretical and a practical standpoint, and I will say something about that in this section.
One convenient thing about flat triangles is that we can see extremely explicitly how subdivision works. Every flat triangle corresponds to a point $(x,0)$ on the bottom of the region $\Sigma$, with $0 \le x \le 1/2$. The following figure will suggest what the "triangles" in the subdivision are.

A flat triangle is a set of three points, not all the same, in a line. One can transform a flat triangle so that its vertices are $(0,0)$, $(1,0)$, $(x,0)$ with $0 \le x \le 1/2$ - i.e. so that $x$ is on the bottom of $\Sigma$. Using labeling introduced earlier, the figure should help you see that the vertices of the barycentric subdivision are: $$ \eqalignno { \Delta_{1} &\colon 1/2 & 1/2 - (x+1)/3 & (x+1)/3 \cr \Delta_{2} &\colon 1 -(x+1)/3 & 1/2 - (x+1)/3 & 1/2 \cr \Delta_{3} &\colon 1-(x+1)/3 & 1- (x+1)/2 & (x+1)/2 - (x+1)/3 \cr \Delta_{4} &\colon (x+1)/2 - x & (x+1)/3 - x & (x+1)/2 - (x+1)/3 \cr \Delta_{5} &\colon (x+1)/3 - x/2 & (x+1)/3 - x & x/2 \cr \Delta_{6} &\colon (x+1)/3 & (x+1)/3 - x/2 & x/2 \cr } $$
For $0 \le x \le 1/2$ all of these are non-negative, and in every case the first is the longest "side" (which is therefore the sum of the other two). Which is the shortest side is not the same for all. The point of $\Sigma$ corresponding to each of these turns out to be $$ \eqalign { \Delta_{1} &\colon \; { 1 - 2x \over 3 } \cr \Delta_{2} &\colon \; { 1 - 2x \over 4 - 2x } \cr \Delta_{3} &\colon \; { 1 + x \over 4 - 2x } \cr \Delta_{4} &\colon \; { 1 + x \over 3 - 3x } \quad (x < 1/5) \cr & \phantom{\colon} \;\> {2 - 4x \over 3 - 3x } \quad (x \ge 1/5) \cr \Delta_{5} &\colon \;\> { 3x \over 2 - x } \>\quad (x < 2/7) \cr & \phantom{\colon} \;\> {2 - 4x \over 2 - x } \quad (x \ge 2/7) \cr \Delta_{6} &\colon \;\> { 3 \over 2 + 2x } \cr } $$
We can see how this works out by plotting the quantities in these columns as a function of $x$ over the range $[0, 1/2]$. For example, let's look at $\Delta_{5}$. Here are graphs of the "sides" of $\Delta_{5}$, plotted as a function of $x$ in the range $[0,1/2]$:
Thus the third column is smallest in the range $[0, 2/7]$, and second in the rest.
These explicit values make it relatively simple to see what is going on for flat triangles. To each $i = 1$, ... , $6$ we have a map from $[0,1/2]$ to itself, and these are graphed in the following figure:
Final remarks
A number of things about the shapes one gets by barycentric subdivision of a triangle have been proven, but some of the most interesting questions do not seem even to have been approached. Here are a few that stand out:
- Are the circles one sees an artefact, or is there an interesting explanation of them? As far as I can tell, they are a completely new phenomenon.
- The shapes form a kind of wave flowing down to the bottom of $\Sigma$. Can one find explicitly the asymptotic form of this wave? I am not familiar with anything like this in the current mathematical literature. What one might hope is that what we are seeing here is a kind of universal process, a dynamic analogue of the central limit theorem, which explains why the normal curve is ubiquitous. Of course the answer will depend on the form of the stable distribution on the flat triangles.
- Are there other examples of similar probabilistic flows?
I haven't said anything about how the known facts have been proved. The common technique in all cases is a clever transformation of the random walk to a question concerning the product of random $2 \times 2$ matrices, about which a lot has been known for a long time. I do not see, however, how this technique could tell us anything about the problems posed above.
Comments?
Reading further
There is not much literature on this topic, and---as far as I can tell---nothing except research publications.
- Amie Wilkinson, `What are Lyapunov exponents, and why are they interesting?', Bulletin of the American Mathematical Society 54, pages 79-106.
It was this article that brought to my attention the problems of barycentric subdivision. The Lyapunov exponent in play here is the logarithm specifying the geometric progression of means mentioned above.
- Bob Hough, `Tessellation of a triangle by repeated barycentric subdivision', Electronic Communications in Probability 14 (2015), 270-277.
- Imre Barany, Alan F. Beardon, T. K. Carne, `Barycentric subdivision of triangles and semigroups of Möbius maps', Mathematika 43 (1996), 165-171.
This is, I believe, the first investigation of the dynamics of barycentric subdivision.
- Persi Diaconis and Laurent Miclo, `On barycentric subdivision, with simulations'.
This is the most thorough investigation in the literature.
- Child plot animation. A file that I have made illustrating through `page turning animation' how the formation of children behaves for different points of $\Sigma$. Keep in mind when looking at it that the graph of any transformation from 2D to 2D sits in 4D, and hence illustration is intrinsically difficult for humans.
Acknowledgement
I have benefited greatly from discussions with my colleague Gordon Slade.
Comments?
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
Email Bill Casselman


 Bill Casselman
Bill Casselman