
Assessing Student Learning
Assessment refers to the system of processes and tools used to understand and measure student progress. Assessment provides windows into your students' progress toward learning goals, and ultimately helps students understand "Have I learned what I need to learn?"
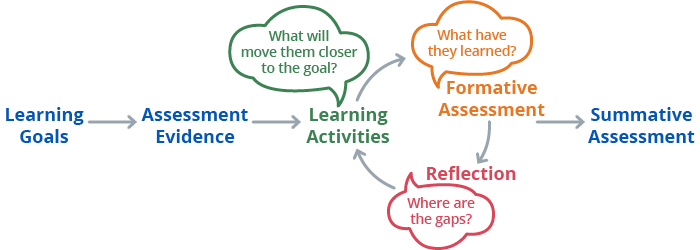
Two things are necessary to be able to understand this progress: a clear statement of learning goals, and a means to measure growth (assessments). Once you identify the assessments you will use to measure student learning, you can then identify the learning activities (lectures, projects, homework, group work) that will help students’ understanding and skills move them toward the learning goal. This backward design model requires you to start from the goals, and work your way back to the learning activities that support them.

Step 1: Set learning goals: What do you expect your students to be able to do?
A learning goal focuses on student learning, rather than coverage of material. Learning ultimately depends on students’ development of skills and understanding, and doesn't happen simply because they've been exposed to material. Articulating which skills and understanding we want students to develop allows us to create assessments that track their progress toward those goals. Read more . . .
Goals-based teaching focuses on:
- Students learning significant and appropriate content and skills
- Students learning to think for themselves and solve problems in the discipline
- Students leaving the course prepared to use their knowledge and skills
A learning goal should be concrete, measurable, and focus on what students will be able to do at the end of your course, unit, or class session. For example,
“My students will understand that the derivative of a function measures the slope of the line tangent to a function at a point, and will be able to use this concept to graph polynomial functions.”
Note that this goal is about what the student can do, not what will be taught. Because it is a specific descriptions of what students will be able to do, it can be measured. That measurement is the purpose of assessment.
There are several types of goals that you may emphasize at different points in instruction. Learning mathematics often includes a mix of acquiring facts, skills, knowledge, or concepts. For example:
- Students will be able to define the inverse of a matrix (fact)
- Students will be able to compute the inverse of a matrix and identify if two matrices are inverses of each other (skill)
- Students can describe the meaning of an inverse matrix (knowledge)
- Students will be able to use a matrix inverse in the algebraic structure of a vector space (concept)
What do you want your students to be able to do? Identify these goals for yourself, and communicate it to your students. These learning goals can then be the underpinning of your course and serve as the basis for developing learning and assessment activities to meet those goals.
How can you engage students in reflection about and communication of mathematics?
Which course activities can help students understand mathematics?
Which forms of assessment provide insight to skills, knowledge, and concepts?
How can assessments provide feedback to you and to them?
Do students have access to the tools they need?
Step 2. Align assessment with goals: How can assessment provide evidence of students' progress toward these goals?
Assessment typically plays two roles in instruction. Formative assessment is a set of practices that give both you and your students feedback on the their progress toward learning goals. Summative assessments measure whether students have achieved the learning goals at the end of a course, unit, or lesson. Read more . . .
Formative assessments
- Occur throughout a class or course
- Measure students' progress
- Provide feedback to teachers and students about their learning
- Seek to improve students’ growth toward learning objectives
- Can be graded or ungraded
Summative assessments
- Occur at the conclusion of a lesson, unit or course
- Measure student achievement
- Usually graded and often heavily weighted (but don’t have to be!)
Learning activities, formative assessment, and reflection are three parts of an ongoing cycle in goals based learning and assessment. For example, working on a project can help students learn, and at the same time, give you and them feedback on what they understand. Reflecting on the project as they work though it can lead the instructor to create or refine learning activities, and the students to focus their efforts.
Summative assessment can then provide a summary assessment of student progress at several milestones throughout the course.
Assessment tips and strategies
Have a library of assessment tools and learning activities in mind, so you can choose what works best for the facts, skills, knowledge, and concepts you want students to learn.
Avoid assessing too many things in one activity. If the student is unsuccessful, it may be hard to discern what they know and what they don't.
With multiple choice questions:
- Create distractors (the incorrect choices) that diagnose students' misconceptions .
- Avoid “all of the above” and “none of the above”—these are essentially a series of true-false questions, and can be linguistically complex.
Use unambiguous language and avoid double-negatives or other complex sentence structures (Which of the following is not true for all real values of x?).
Consider allowing students to revise and resubmit work so they can learn from their errors.
Balance good assessment practices with what is realistic to grade.
Identify for yourself and your students why the assessment structures (e.g. open book, time limits, use of calculators),are important to the things you want to assess.
Read below to find assessment models.
Step 3: Develop Learning Activities
Identifying what you want students to learn and how you will be able to assess their learning can inform how you develop activities that will help them learn. Here are some examples that go beyond traditional exams and homework problems. Many of these can be used for either formative (during learning) and summative (evaluating learning) assessment. Many of the assessment models listed here are also learning activities--as learning and assessment occur simultaneously, as students see what they are learning and can adapt strategies to better reach their goals. Read more . . .
Ask students to think about and communicate what they know:
- Reflect on what you’ve learned.
- Identify and correct errors, and re-submit revised work
- Justify the steps in a solved problem and identify errors.
- Correct or confirm a counterexample to a statement.
- Describe three important concepts you’ve learned and provide an example of each.
- Summarize ideas on an Empty Outline after a lecture or textbook chapter. An Empty Outline is provided by the instructor to guide students in organizing their understanding of a topic as they learn it.
- Identify the Muddiest Point in a lecture, discussion, or assignment
- Write a minute paper--a brief assignment that can address concepts and skills.
- Decide if a given statement is true. If it is true, give an example. If false give a counterexample.
Tools to encourage reflection and communication:
- Polling
- 321 exit ticket: 3 things I learned, 2 things that were interesting, 1 question I have.
- Twitter model: tell me in 75 words or less . . . .
- Presentations connecting what you’ve learned to ideas from another course or discipline.
- Oral presentation about a topic. You might grade the presentation based on how well other students understand.
- Projects, either alone or in groups.
- Portfolios to showcase learning achievements.
- Allow students to choose between taking a final exam and completing a project.
- Videos explaining how they solved a problem, or answering one of the questions above.
Rubrics for formative feedback
Rubrics provide formative feedback, and make grading easier and more consistent. They also communicate clear expectations to students, to allow them to focus on your learning goals. A rubric is a tool that delineates performance expectations, usually along several dimensions—for example, use of definitions, reasoning, communication, correct solution. A rubric includes clear definitions of each dimension and of the criteria that define levels of mastery, and identifies the weight given to each dimension. Rubrics can be used for any type of assessment: projects, presentations, class participation, exams, portfolios, etc. Rubrics are often used separately for each problem on an assignment.Read more . . .
Rubrics have several advantages for both instructors and students:
- Particularly with long assignments or in large classes, grading consistency can difficult to maintain over time due to fatigue or shifting standards based on prior experience. The rubric descriptions help grading standards remain more efficient and consistent.
- Rubrics are invaluable in large courses that have multiple graders because the clearly defined criteria reduce systematic bias among graders.
- Rubrics communicate to students the specific requirements and acceptable performance standards of an assignment, so they know your expectations and can prepare accordingly.
- Used in formative assessment, rubrics allow instructors to monitor and assess students' progress as they work toward clearly-defined goals. By reviewing the component scores, instructors can identify the skills or concepts that need more instructional time.
- Students can more easily recognize their strengths and weaknesses and direct their efforts accordingly.
Rubrics can be relatively simple, defining the dimensions and the criteria for full credit.

Or a rubric can provide specific detail about point levels, with the anchors in each row ensuring greater consistency while allowing graders to assign the full range of points.
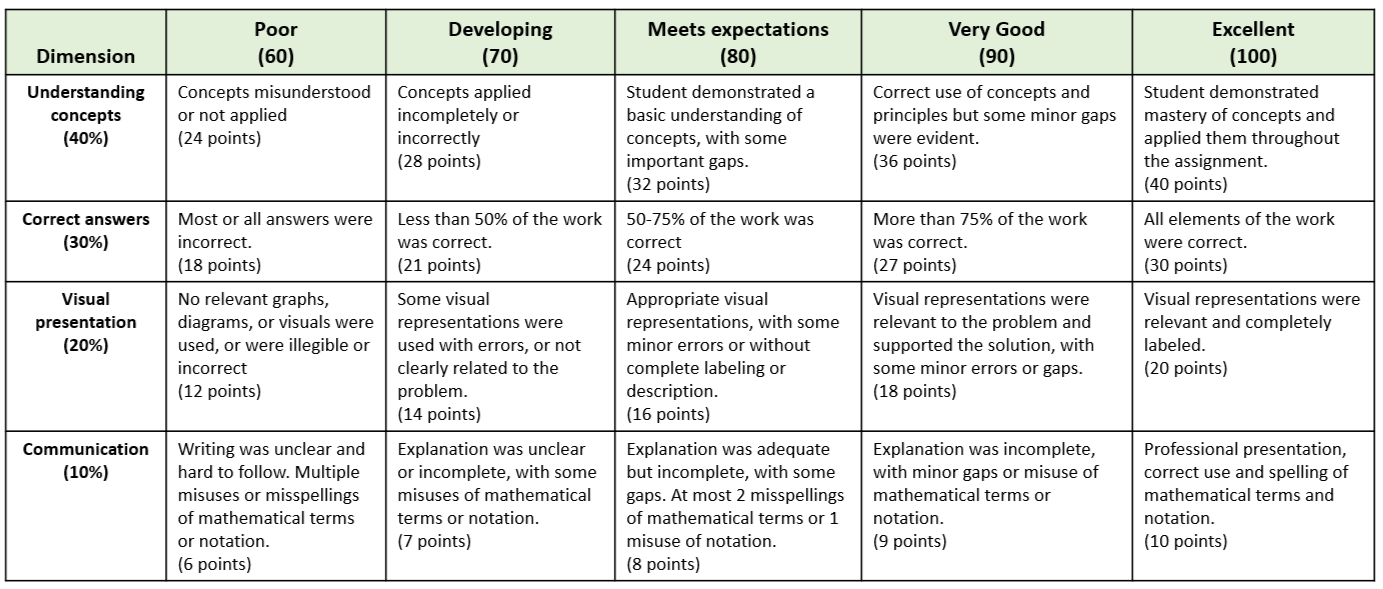
There are many styles and structures of rubrics. Your college or university might have a standard format they prefer, or you can work with colleagues or look online.
Additional learning and assessment resources
Mathematics Assessment Project
The Eberly Center at Carnegie-Mellon University's Assess Teaching and Learning
7 Exam Questions for a Pandemic (or any other time) by Francis Su
COVID-19 Exposes Mathematics Education Inadequacies: A modicum of (secret) relief for Educators by James Tanton
Quality Matters Research Library – the research basis for Quality Matters online and hybrid course standards
The Educause Library links to evidence-based articles and publications related to teaching and learning with technology, particularly in the hybrid and online modalities
For more about teaching and learning mathematics, visit our Teaching Resources page.

