Solar Daze
How can one understand the variation in the length of a solar day? ...
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
Email Bill Casselman
Introduction
Noontime marks the moment halfway through the day, when the Sun reaches its highest point in the sky. Noontime differs for different locations on Earth, which is why the planet is partitioned into time zones. This is easily understood as a necessary feature of the Earth's rotation and spherical shape. But there is another curious thing about noontimes that is not so apparent---if you measure the length of a day as the difference in time recorded on your watch between one noontime and the next, which is called the length of the solar day, you will see that this difference varies throughout the year.
The variation is not very large---a matter of a few dozen seconds at most---and to tell the truth you will have to make awfully accurate measurements in order to see it, since a few seconds of time amount to a difference of roughly one percent of the width of the Sun. Nonetheless the differences accumulate, and this is why reading time accurately from a sundial requires adjustment. Considering how small the effect is, and how difficult to measure, it is astonishing that Greek astronomers of the Hellenistic era were perfectly aware of it and knew a reasonably accurate way to calculate it.
How can one understand the variation in the length of a solar day? There are two main causes. One is that the axis around which the Earth rotates is not perpendicular to the plane in which the Earth rotates around the Sun. Equivalently, the plane of the earth's equator is inclined to the plane of the earth's orbit. The other is that the Earth's orbit around the Sun is not a true circle. This means, according to one of Kepler's Laws, that its speed in orbit and hence the apparent motion of the Sun is not constant. Understanding the first of these is a matter of spherical trigonometry. It is the second that I'll be concerned with.
The geometry of orbits
Kepler's First Law is that the orbit of a planet is an ellipse with the Sun at one of its foci. What does this mean?
An ellipse is a squashed circle. In other words, start with a circle and compress it uniformly, say vertically. For example, if you start with a circle of diameter $2$ and compress it by a factor of $2$, you get an ellipse whose long axis has length $2$ and whose short axis has length $1$. In general, if the original circle has equation $x^2 + y^2 = a^2$, then the ellipse will have equation $(x/a)^{2} + (y/b)^{2} = 1$, where now $2b$ is the length of the short axis. The compression factor is $b/a$. This compression changes the area of the circle from $\pi a^{2}$ to $(b/a) \cdot \pi a^{2} = \pi ab$.


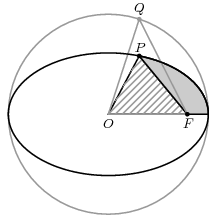
The ellipse has one remarkable feature. There exist two points on the major axis, called the foci (plural of focus) with the property that a line drawn from one focus to the ellipse itself and then to the other focus has constant length. If this focus is at $(f,0)$ then as the figure on the right shows that $b^2+f^2= a^2$, so $$ 2\sqrt{b^{2} + f^{2}} = 2a, \quad f = a\sqrt{1 - (b/a)^{2}} \, . $$
The quantity $e = \sqrt{1 -(b/a)^{2}}$ is called the eccentricity (i.e. "off-centeredness") of the ellipse. It is $0$ if the ellipse is in fact just a circle, and it is near $1$ if $b/a$ is very small and the ellipse is very elongated. The foci are thus at positions $(\pm ae, 0)$.
The ratio $b/a$ is equal to $\sqrt{1- e^{2}}$, which is approximately $1 - e^{2}/2$ if $e$ is small. The difference between this and $1$ is of second order in $e$, and ellipses with eccentricities of reasonable size look quite circular. For example, the eccentricities of the orbits of Mercury (with the most eccentric orbit of all planets, unless you believe that Pluto is a planet), Earth, and Mars are $0.2$, $0.0167$, and $0.09$, and here is what they look like:
The deviation from circularity is not noticeable, but the eccentricity of the focus is clearer.
Comments?
Motion on the orbit
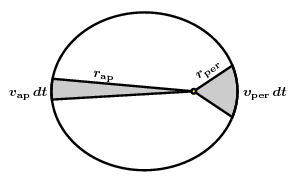
Kepler's Second Law asserts that as a planet travels in its orbit around the Sun, equal areas are covered in equal times. The area meant here is the area swept out by the radius from the planet to the Sun, like this:
One immediate consequence of the Second Law is that the radial area swept out by the planet is proportional to time, and more precisely that the area swept out in time $t$ is equal to $\pi ab (t/t_{\rm period})$. This law therefore determines relative speeds on the orbit. The two simplest cases are at perihelion (where the orbit is nearest to the Sun) and at aphelion (where it is farthest away from it).
If we apply Kepler's Law at both these times over some small time interval, we see that $$ v_{\rm per} \, r_{\rm per} \, dt = v_{\rm ap} \, r_{\rm ap} \, dt, \quad { v_{\rm per} \over v_{\rm ap}} = { r_{\rm ap} \over r_{\rm per} } = { 1 + e \over 1 - e } \, . $$
At perihelion, the radius is least, so that the speed is a maximum. Similarly, at aphelion it is a minimum.
The ratio of speeds at perihelion and aphelion is easy to figure out. With a little more work, as I'll explain later on, we can obtain formulas for the speeds themselves:
Theorem. The orbital speed at perihelion is $$ { 2 \pi a \over t_{\rm period} } \sqrt{ 1 + e \over 1 - e} \, , $$ and that at aphelion is $$ { 2 \pi a \over t_{\rm period} } \sqrt{ 1 - e \over 1 + e} \, . $$
These are consistent with Kepler's Law since the ratio of these two terms is, as it ought to be, $(1 + e)/(1-e)$. As another check on this, set $e=0$. In this case, the planet orbits in a circle at constant speed. The two formulas agree and give as that speed $$ { 2 \pi a \over t_{\rm period} } = { \rm circumference \over t_{\rm period} } \, . $$
Since the corresponding radii are $a(1 \mp e)$, the corresponding angular velocities are $$ \eqalign { & { 2 \pi \over t_{\rm period} \, (1 - e) } \;\, \sqrt{ 1 + e \over 1 - e} \cr & { 2 \pi \over t_{\rm period} \, (1 + e) } \;\, \sqrt{ 1 - e \over 1 + e} \, . \cr } $$
Solar days
As a planet traverses its orbit, it spins on its axis. There are two ways to measure this spin---depending, you might say, on your point of view. If you are on the planet, the entire sky seems to be rotating. The Sun in particular rises in the morning, sinks in the afternoon, and disappears from sight, on a more or less periodic schedule. How to make this precise? A meridian transit is the moment when the Sun reaches a maximum height in the sky---i.e. when it transits your meridian, which is in effect the plane passing through you, the planet's center, and the poles. Projected onto the celestial sphere, it is a circle in the sky that bisects the sky into two equal halves. The solar day is the length of time it takes from one meridian transit to the next.
But if you are sitting way up in the sky---far above the planet's orbit, in fact---you will see the planet rotating with respect to the (more or less) fixed stars. A sidereal day is the amount of time it takes for one of these rotations. In the following diagrams, I am looking at a rather simple planet, one whose equatorial plane is the same as the plane in which its orbit lies---a two-dimensional planet, one that only a mathematician could love. The model planet in the diagram below takes six sidereal days to traverse the orbit, traveling counter-clockwise ...
... but only five solar days:
Noon takes place at approximate sidereal times $t=0$, $1.3$, $2.5$, $3.5$ and $4.7$, making solar days of lengths about $1.3$, $1.2$, $1.0$, $1.2$, and $1.3$ as measured in sidereal days. But sidereal time is true time, the time measured nowadays (ignoring some little shudders of the planet every now and then) by atomic clocks. Sure enough, the length of solar days measured by clocks is not a constant.
It is always true that if a planet takes $N$ sidereal days to traverse its orbit, it takes $N-1$ solar days. Even if $N$ is not an integer.
Comments?
A quantitative estimate
How can we make an estimate of the variation of the length of solar days? It is not too difficult to do this in very elementary terms.
Let's look at another example. Here, the eccentricity of the orbit is $0.6$, and our planet takes $40$ sidereal days to traverse the orbit. In the following diagram, the planet is plotted at intervals of one sidereal day.
Just to check how things are going, you can verify that the speed at perihelion does indeed seem to be about $4 = (1+e)/(1-e)$ times that at aphelion. We ask, what is the length of one solar day at perihelion? To answer this, we use a trick. Think of an imaginary planet whose orbit is a circle around the focus with radius $r_{\rm per}$, and whose constant speed is the same as that of the original planet. we also plot its orbit at intervals of one sidereal day. Then we do the same for aphelion:
These imaginary planets will rotate at the same rate as the original. The length of one of their solar days is the same as that of the original at the appropriate moment. If $N$ is the period of the orbit of one of these imaginary planets, then the length of one of its solar days (in terms of sidereal days) is $$ { N \over N - 1 } \, . $$
So we ask, what are the values of $N$?
Theorem. The period of the imaginary planet associated to perihelion (as measured in sidereal days) is $$ N (1 - e) { \sqrt{ 1 - e \over 1 + e } } \, . $$ and that of the imaginary planet associated to aphelion is $$ N (1 + e) { \sqrt{ 1 + e \over 1 - e } } \, . $$
Here, too, a rough check can be made. The ratio of angular velocities at perihelion and aphelion is $\gamma^{2}$ where $\gamma = (1+e)/(1-e)$ (the speed is greater at perihelion, but the radius is smaller). But this is also the ratio of $N$ values: $$ N_{\rm ap} = \gamma^{2} N_{\rm per}\, . $$
In general, let $N$ be the number of sidereal days in one orbit. The ratio of longest solar day to shortest one is then very close to $$ { N_{\rm ap} / ( N_{\rm ap} - 1 ) \over N_{\rm per} / ( N_{\rm per} - 1 ) } = { 1 - { 1 \over N_{\rm per} } \over 1 - { 1 \over \gamma^{2} N_{\rm per} } } $$
If $N$ is large, as it is for Earth, the ratio of longest to shortest is about $$ { 1 - { 1 \over N } \over 1 - { 1 \over \gamma^{2} N } } $$
In the example with $e=0.6$ we get approximate values of $8$ and $128$ for $N$. This makes the solar day at perihelion approximately $8/7$ sidereal days, while that at aphelion is approximately $128/127$.
For Earth, $N = 366.2422$ (i.e. about $365 \; 1/4$ solar days) and $e = 0.0167$. The ratio of longest to shortest is about $1.000177$, and this works out to a difference of about $15$ seconds between the shortest and longest solar days, as far as the contribution from the variation of Earth's orbital speed is concerned.
We have been looking at a two-dimensional planet, but the basic idea for one in 3D whose equator is inclined to its orbit is not very different. Instead of seeing how the meridian line sweeps out to cross the Sun, you look at the plane through a meridian and the planet's center.
Kepler's equation and orbital speed
At time $t$, let $E(t)$ be the angle of the point on the circle of radius $a$ that gets squished down to the point $P(t)$ on the elliptical orbit at time $t$.
On the one hand, Kepler's Second Law says that $$ A = \pi a b ( t / t_{\rm period}) \, . $$
On the other, the area $A$ is equal to $b/a$ times the area of a region cut on the circle of radius $a$ that gets squished: $$ A = (b/a) ( \pi a^{2} (E / 2 \pi) - (1/2) \, ae \cdot a \, \sin E ) \ . $$
If we equate these and rewrite we get $$ M(t) = { 2 \pi t \over t_{\rm period} } = E(t) - e \sin E(t) \, . $$
This is Kepler's equation. It might seem to you a bit puzzling---it enables you to tell what $t$ is if you are given the point $E$, but of course what you really want to know is the opposite. There is in fact no good formula for $E(t)$ as a function of $t$, but there are many methods to calculate it for any given $t$. We shan't need to know them (although the orbital plots shown throughout this column certainly use one of these methods).
To find velocities, we continue: $$ \eqalign { M(t) &= { 2 \pi t \over t_{\rm period} } \cr &= E(t) - e \sin E(t) \cr M' &= 2 \pi / t_{\rm period} \cr &= E' ( 1 - e \cos E ) \cr E' &= { 2 \pi \over t_{\rm period} \; (1 - e \cos E) } \cr P(t) &= (a \cos E, b \sin E) \cr P'(t) &= (-a E' \sin E, b E' \cos E) \cr &= a E' ( -\sin E, \sqrt{1 - e^2} \cos E ) \cr &= { 2 \pi a \over t_{\rm period} }{ 1 \over 1 - e \cos E } \; ( -\sin E, \sqrt{1 - e^2} \cos E ) \; . \cr } $$
Setting $E = 0$ (perihelion) and $E = \pi$ (aphelion) we get $$ \eqalign { P'(0) &= { 2 \pi a \over t_{\rm period} } (0, \sqrt {1 + e} / \sqrt{ 1 - e } ) \cr P'(\pi) &= { 2 \pi a \over t_{\rm period} } (0, - \sqrt { 1 - e} / \sqrt{ 1 + e } ) \, , \cr } $$
The orbital speeds are the $y$-components of these velocities.
Comments?
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
Email Bill Casselman


 Bill Casselman
Bill Casselman