Crochet Topology
This note continues the tradition of the interaction of math and crafts by using crochet to explore and understand map coloring on surfaces....
Edited by Tony Phillips.
Introduction
Crafts have been interacting with math, and math education, for centuries. A few examples (in no particular order) are:
This column continues the tradition by using crochet to explore and understand map-coloring on surfaces. The outer layer of any solid object (for instance, an egg, a donut, a pretzel) is an orientable surface. A famous example of an unorientable surface, with boundary, is the Möbius strip (see below). Unoriented surfaces without boundary are harder to visualize because they do not "live" in our three-dimensional space. One of the best known is the Klein bottle, which can only be depicted in 3D by making it intersect itself. In its native state there is no such self-intersection.

The Klein bottle. Image by Tttrung, from Wikimedia Commons.
The map-coloring problem involves two related but different questions:
Question 1: What is the largest number of regions into which one can divide a given surface so that every two regions share a segment of boundary? (Such a partition has been called a complete map).
Question 2: What is the smallest number of colors needed to paint any map on a given surface so that every two regions that share a segment of boundary have different colors?
We can take "region" to mean a (curvilinear) polygon (in the language of topology, it must be connected and simply-connected).
The genus of an orientable surface is its number of "handles." For instance, the sphere has zero handles and the torus (that is, the skin of a donut) has one handle. There is a slightly more complicated definition for non-orientable surfaces.
Consider any partition of a surface $S$ into polygonal regions. The regions intersect along edges, and the edges meet at vertices. Denote by $V$ the number of vertices, $E$ the number of edges and $F$ the number of regions. Amazingly, the number $V - E + F$ does not depend on the partition; it is called the Euler characteristic of $S$, denoted by $X(S)$, and for orientable surfaces is related to the genus by $X(S)= 2-2g$. For more details on the Euler characteristic see the Feature Columns by Joseph Malkevitch and Tony Phillips.
Let's denote the answer to Question 1 for a surface $S$ by $R_{\max}(S)$ and the answer to Question 2 by $C_{\min}(S)$. Since the partition of a surface considered in Question 1 is one of the (many) maps considered in Question 2, it follows that $R_{\max}(S) \leq C_{\min}(S)$.
After many decades of work by mathematicians (both professional and amateur), there is complete answer to both questions. Define $$H(S) = \left \lfloor{ \frac{7+\sqrt{49-24 X(S)}}{2} }\right \rfloor, $$ where $\lfloor x \rfloor$ means the largest integer no larger than $x$. Then $$R_{\max}(S) = C_{\min}(S) = H(S) $$ for all surfaces except the Klein bottle $K$, for which $R_{\max}(K) = C_{\min}(K) = 6$, whereas $H(K)=7$.
The table below shows the value of $R_{\max}(S) = C_{\min}(S)$ for some examples of $S$.
$$\begin{array}{|l|c|c|}\hline \mbox{Surface}~~S& X(S)& R_{\max}(S) = C_{\min}(S)\\\hline \mbox{Sphere}& 2& 4\\\hline \mbox{Klein bottle}& 0& 6\\\hline \mbox{Torus}& 0& 7\\\hline \mbox{Projective plane}& 1& 6\\\hline \mbox{Genus 2, orientable}& -2& 8\\\hline \mbox{Genus 3, orientable}& -4& 9\\\hline \end{array}$$
History
The map-coloring problem has a, yes, colorful history. Questions 1 and 2 were occasionally confused or merged and for many years partial or total answers were claimed by amateur and professional mathematicians, occasionally convincing the mathematical community that the problems had been solved.
The Four-color Problem
The question for the sphere $S_0$ (0 for the genus) was the most natural, since it involved maps on surfaces like the Earth, but turned out to be the most difficult. For the sphere, the answer to Question 2 became the Four-color conjecture: Any map on the Earth can be colored with four colors so that no two regions that share a boundary segment have the same color.
Note that since puncturing a sphere does not change map-coloring properties, the answer to Question 2 is the same for the sphere and the plane.
1840. The first recorded mention of Question 1 was made by August Möbius in one of his lectures in 1840, where he teased his students by asking: There was once a king in India who had a large kingdom and five sons. In his will he decreed that, after his death, the kingdom should be divided among his sons in such a way that the territory of each should have a common boundary line (not merely a point) with the territories of the remaining four. How could this be done? In the next lecture he revealed that such a partition does not exist. (This story is recounted by H. S. M. Coxeter in The Mathematics Teacher, 52 (1959) 283-289).
- Möbius probably had in mind an elementary argument based on the Euler characteristic, like the following: we can assume $(*)$ that each vertex is incident to at least three edges; in fact, a vertex incident to only two can be eliminated, along with one edge, without changing the map or the Euler characteristic $V-E+F=2$ for the sphere. Also we know that each of the five regions has at least four edges; since each edge is shared by two regions, it follows that $E\geq 10$. On the other hand using $F=5$ the Euler characteristic gives $V=E-3$; also, since each edge has two ends, $(*)$ implies $3V\leq 2E$. Given that $3V = 3E -9$, we get $3E -9 \leq 2E$ or $E\leq 9$, a contradiction. Note: this argument just means that the sphere admits no complete map with 5 regions, and does not give any information, one way or the other, about the existence of a non-four-colorable map.
1852. In 1852, Frederick Guthrie, who went on to found the Physical Society of London, mentioned Question 2 (for maps of the plane) to his professor, Augustus de Morgan. According to Guthrie, the conjecture that four colors were always sufficient (in our notation, that $C_{\min}(S_0)=4$) had been originally formulated by his brother Francis, who came up with it while coloring maps of England.
A persistent (and somewhat pleasant to believe) rumor circulated for years among mathematicians, that cartographers had experimentally at arrived at the "Four color conjecture" (i.e. $C_{\min}(S_0)=4$). But as Kenneth May explained there is no evidence to support it.
1977. Guthrie's conjecture, that any map on the plane (or the sphere) does not need more than four colors to be "properly" painted became the renowned Four Color Theorem, whose elusive proof generated a great deal of wonderful mathematics (including many, many fallacious proofs) until finally the matter was settled by a computer-assisted proof (Appel and Haken, 1977). A recent student project at the Illinois Geometry Lab, led by Jeremy Tyson, catalogued documents donated by Appel's widow; they are now available at the Illinois University Library. Here is one of the drawings from the collection.
Some of Appel's sketches for the four color problem. Illinois University Library, used with permission.
With all the respect that this remarkable achievement deserves, many of us are still hoping for proof, without computer assistance, that might better illuminate the underlying mathematics.
Generalization to other surfaces
1878, 1879, 1890. The four color problem was communicated to the London Mathematical Society by Arthur Cayley in 1878. Possibly in one of Cayley's lectures, Alfred Kempe heard about the problem. Kempe was a barrister who also made interesting contributions to mathematics (he claimed that he relaxed by doing mathematics!). One of these contributions was a proof of the four color theorem he published in 1879. The mathematical world sighed then with relief (and possibly with a bit of jealousy); until 1890 when Percy Heawood showed that there was a mistake in Kempe's proof (but he described how Kempe's arguments could be salvaged to prove that $C_{\min}(S_0) \leq 5$). Heawood stated Question 2 and studied it for other orientable surfaces: he introduced the function we have called $H(S)$, and proved $C_{\min}(S)≤H(S$) for any orientable S. He was under the impression thay he had proved equality, but this is not the case: the only surface for which he did prove equality is the torus, where he gave an example that implies $R_{\max}(\mbox{Torus})\geq 7$.

Heawood's original map: seven regions on the surface of a torus; any two share a boundary segment. From P. J. Heawood, Map-Colour Theorem, Quarterly Journal of Mathematics 24 332-338 (1890).
1891-1968. Early in the history of these ideas the inequalities $C_{\min}(S_0)\geq 4$ and $C_{\min}(S)\leq H(S)$ were established (with no great difficulty) for all surfaces $S$ different from the sphere. As we have seen, the example for the torus showing that $C_{\min}(\mbox{Torus})=7$ was described by Heawood in 1890. Clearly, to establish $C_{\min}(S)\geq H(S)$ it is enough to exhibit a particular example of a complete map on $S$ with $H(S)$ regions. In 1891 L. Heffter found such examples for orientable surfaces of genus 2, 3, 4, 5 and 6, as well as other genera satisfying certain number-theoretical properties. The complete solution for genus different from zero is explained by Gerhard Ringel and J. W. T. Youngs in a 1968 article in the Proceedings of the National Academy of Sciences.
The sphere took almost another decade to settle; it was completely different from all the other surfaces in the techniques required. Nevertheless it is suggestive that the same formula $C_{\min}(S)= H(S)$ holds for all surfaces (except for the Klein bottle). Maybe some day we will find a unified proof for all these cases.
The Torus
In crocheting a complete seven-color map on the torus, it seems natural to work with hexagons, since each region borders six others. We start with seven hexagons of different colors, arranged as follows

Seven-color Honeycomb.
and sew pairs of opposite sides following the edge colors shown: pink with pink, etc., without twisting (so arrows must match).
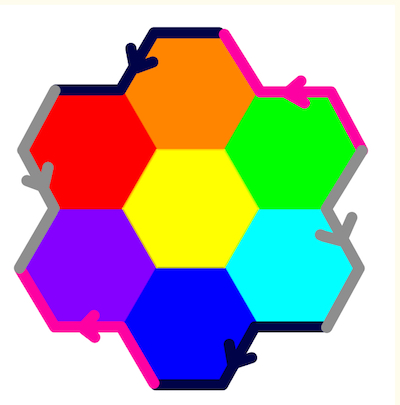
Seven-color Honeycomb, guide for assembly.
The result is indeed a complete seven-color map on the torus, although fairly hard to understand. (Exercise for the reader: Find all possible glueings of pairs of edges of the "hexagonal flower" above that yield a torus). At first sight, it is not even clear that the resulting shape is indeed a torus.




Four views of the assembled Seven-Color Honeycomb.
Another way to crochet a complete map with seven regions on a torus consists in starting with seven congruent rectangles of different colors, with height about four times the width. We will describe two methods for sewing them together. (Of course, these rectangles are secretly hexagons in the sense each that each of them will share a boundary segment with the other six).
For the first method: Assemble the rectangles end to end so they form one long rectangle:

Then start rolling up the long rectangle






Six stages in the rolling up of the rectangle. To complete the surface, sew the top boundary to the bottom, making sure that the shorter edge of the purple rectangle is sewn to the shorter edge of the yellow one.

A completed example of this method, with different edging and a different set of colors.
Second method: Sew the rectangles together as in the figure below, where the upper border is a set of right isosceles triangles.

Then sew together the two indicated segments (matching the arrows) to obtain a "cylinder."

In the cylinder, each of the colors shares a segment of boundary with two other colors. To obtain a complete map, each color should also share a segment of boundary with four additional colors. This can be achieved by using each of the four free segments in each rectangle appropriately. To start, fold up the bottom boundary of the cylinder so it is inside.

Next, one needs to sew the top boundary of the cylinder to the bottom one. Each of the peaks of the top boundary has to be sewn to an appropriate indentation of the bottom boundary. The Geogebra app below illustrates what is meant by "appropriate." Note that once one top peak and bottom indentation have been matched, the rest of the sewing is determined.
By moving the dot on the sliders we can see the different outcomes of sewing a given peak to each of the indentations.

One way that works is to start matching edges as indicated.

The cylinder with matching edge segments sewn together.

The completed and stuffed seven-color torus.

Another example of this method, with different edging and a different choice of colors.
The genus-two surface
Hermann Tietze devotes two chapters of his beautiful book Famous Problems of Mathematics to discussing Question 1 and Question 2. He gives the example below of a complete map with eight regions on a genus-two surface

A complete map with eight regions on a genus-two surface. This picture was probably dates back to Tietze's Berühmte Mathematische Probleme, originally published in 1911. It appears in (and on the cover of) the translation, Famous Problems of Mathematics, Graylock Press, New York; 2nd edition (1965).
Tietze points out a minor printing mistake, namely a portion of the region b is not painted dark brown as it should be. It is not easy to check that this map is indeed complete, because there are no symmetries to help our reasoning. Susan Goldstine presented a very clear example of a complete map with eight regions on the genus two surface: slice a genus-two surface in half so as to obtain two tori, each with a boundary component. On each punctured torus it is possible to draw a complete map with four regions, with the additional property that each region shares two segments with the boundary circle, as in the figure below: a "long segment" and a "short" one.
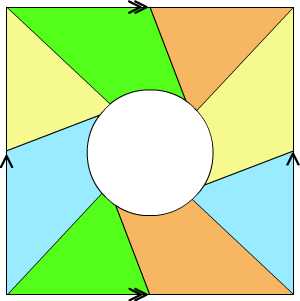
The four-region map on the punctured torus, before and after the identification.
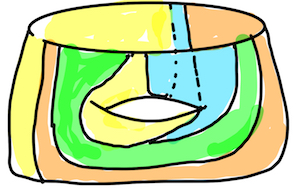
The next step is to assemble these two punctured tori so that the "long" segment of each region touches three of the regions of the other torus and the short segment touches the fourth. (Not every pair of tori can be attached succesfully). Goldstine painted the tea set below to illustrate her genus-two map.

Susan Goldstine's "Tea for eight." From "Capturing Eight-Color Double-Torus Maps", used with permission.
Here is the crochet version.


Two views of an eight-color map on the genus-two surface; each region touches all seven others.
The projective plane and the Möbius band
The projective plane is the surface obtained by attaching a disc to a Möbius band along the boundary. It is non-orientable and, like the Klein bottle, it can't "live" in our 3D space without spurious self-intersections, which turn out to be considerably more complicated than those for the bottle. Without building a model, we can understand a six-color map on the projective plane as follows: we start with a six-color map on the Möbius band (see below), and color the attached disc with one of the colors that touched the boundary curve on the band.
For the Möbius band, Tietze found a complete map on six regions (he pointed out that Möbius himself "almost" had it).
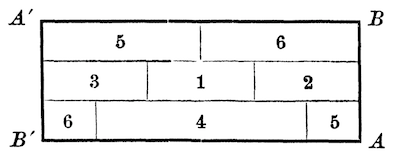
Tiezte's six-color map on the Möbius band. From Famous Problems of Mathematics, Graylock Press, New York; 2nd edition (1965).
Here is Tietze's map implemented in crochet:

Six-color map on the Möbius band.
One way of crocheting the complete six-color map on the Möbius band is to crochet six rectangles and sew them as in the figure below. In this case, it is not possible to have all the rectangles of the same size: The length of each of the "middle" rectangles (light blue, yellow, and green in the example below) is half of that of an "outer" rectangle; their widths are the same.
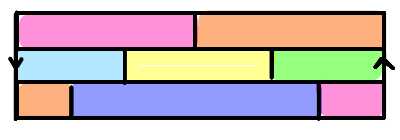
Plan for the six-color Möbius band map in crochet.
The curious exception: The Klein bottle
The Euler characteristic of the Klein bottle $K$ is zero, and so $H(K)=7$. However, Philip Franklin ("A Six-color problem," J. Math. Phys. 13 (1934) 363-369) showed that $C_{\min}(K)=6$. It is the only exception to the rule.



Six-color map on the Klein bottle.
A question for the reader: The genus 3 surface
The map on the genus-three surface below is complete but has only eight regions.




Four views of a complete map with eight regions on a genus-three surface.
Heffter's complete map with nine regions on a genus-three surface is not easy to visualize. His 1890 article in Matematische Annalen describes it by the following table:

Heffter's complete map with 9 regions on the surface of genus 3. The map has 23 vertices (22 tri-valent and one of valence 6). Its 9 octagonal faces are numbered $1, \dots, 9$. For each one, the table lists the cyclic order of the other faces encountered along its border. Corners marked with an arc are those that belong to the valence-6 vertex.
We encourage the reader to try to construct a more geometrically intelligible complete map with nine regions on the genus-three surface, and perhaps to render it in crochet.
Crochet instructions and techniques
Crochet instructions (for right- and left-handed crocheters) can be found in all shapes and forms nowadays, for instance, on YouTube, in web pages, as well as in many, many books.
The author uses the most basic stitch (single crochet) and worsted-weight yarn, with the appropriate crochet hook (yarn often comes with a suggested size of crochet hook.) Any yarn with uniform thickness will do.
The author has a personal preference for crocheting "in circle" as opposed to back and forth, but this is not essential for the final result. Pieces that are crocheted in circle, and use more than one color per row use tapestry crochet techniques, where each stitch has "dominant" color, and the other colors are carried "hidden", as explained, for instance, on this website.
For orientable surfaces, the author uses any stuffing available. The Möbius band and Klein bottle are crocheted by carrying an additional wire "under" the dominant color.
To crochet a Möbius band, start with a standard chain, (which will play the role of the middle curve of the band) of any reasonable length, say 30 or 40 stitches. Usually, at the end of the chain one should turn the chain and add another row of single crochet. In this case, one has to continue onto the other end of the chain, continuing with a chain stitch, but twisting it 180 degrees (so that the new row will be stitched on the "bottom" of the chain. After this, continue with single crochet and the Möbius band will grow. (The reader will have noticed that this description does not include colors).
A very interesting "recipe" for knitting a Möbius band is given on page 20 of the handouts of Geometry and the Imagination.


 Moira Chas
Moira Chas







































