Does He Have It?
Sensitivity, Specificity, and COVID-19 Testing
As every doctor should know, medical tests are rarely 100% accurate. Interpreting them is a matter of probability. And probability, of course, is a matter of mathematics...
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
Email Bill Casselman
Well, make up your mind. Does he have it or not?
I remarked in an earlier column that there were two major ways in which mathematics has contributed to our understanding of the disease COVID-19 and the coronavirus SARS-CoV-2 that causes it. One was by modeling the development of the epidemic in order to predict possible outcomes, and the other was by uncovering the sources of particular outbreaks by tracking the evolution of genomes. This column will be concerned with a third way in which mathematics helps to control the epidemic, and that is by interpreting procedures that test for the presence of the disease.
The basic problem was illustrated dramatically at the beginning of August. The President of the United States was about to visit the state of Ohio, and naturally it was expected that he and the governor of Ohio (Mike DeWine, a Republican) would meet. As a matter of routine, the governor was tested for coronavirus before the meeting, and the test returned a positive result. It was a definite possibility, even likely, that DeWine was afflicted with Covid-19. He put himself into quarantine immediately, and of course the meeting with the President had to be called off. A short time later a second, presumably more accurate, test was given and this time it came back negative. This second result was later confirmed by third and fourth tests. (You can read more about this incident in an article in The New York Times, or also another NYT article.)
It was suggested in the media (the Washington Post, among others) that this sequence of events would reduce the trust of the population at large in the validity of such tests, and—very, very unfortunately—discourage many from having them. The governor himself, one of the state governors to take the epidemic extremely seriously, stated very clearly that in his opinion avoiding tests was not at all a good idea. Medical experts agree—testing is in fact a crucial tool in controlling the epidemic, and the United States is almost certainly not doing enough of it. At the very least it is doing it awkwardly. It is therefore important to try to understand better what is going on.
The basic fact is very simple: as every doctor should know, medical tests are rarely 100% accurate. Interpreting them is a matter of probability. And probability, of course, is a matter of mathematics.
Measuring a test's accuracy
Many medical tests are abstractly similar: they give a yes/no answer to a question about the status of a patient. In the case of the governor of Ohio, the question is, "Does this person have COVID-19?" His first test answered "yes", while the later three answered "no". Clearly, they were not all correct. The tests are certainly inaccurate a certain percentage of the time.
How is the accuracy of such tests measured? There is no single number that does this. Instead, there are two: sensitivity and specificity. To quote one instructive web page, sensitivity and specificity "are the yin and yang of the testing world and convey critical information about what a test can and cannot tell us. Both are needed to fully understand a test's strengths as well as its shortcomings."
Sensitivity characterizes how a test deals with people who are infected. It is the percentage of those who test as infected when that they are in fact infected. A test with high sensitivity will catch almost every infected person, and will hence allow few of those infected to escape detection. This is the most important criterion. For example, it was reported recently that Spanish health authorities returned thousands of tests to one firm after finding that its tests had sensitivity equal to 30%. This means that 70% of infected people would not be diagnosed correctly by this test.
Specificity characterizes how a test deals with people who are not infected. It is the percentage of those who will test as uninfected when they are in fact uninfected. A test with high specificity will hence report a small number of false positives.
For detecting currently infected people, high sensitivity is important, because infected people who avoid detection (false negatives) are potential sources of further infection. High specificity is not so crucial. Tagging uninfected as infected (making false positives) can be unfortunate, but not with possibly fatal consequences.
It might not be immediately apparent, but sensitivity and specificity are independent features. For example, it could happen that a test lazily returns a "yes" no matter what the condition of the patient happens to be. In this case, it will have sensitivity 100%, but specificity 0%. Or it could behave equally lazily, but in the opposite way, and return a "no" in all cases: sensitivity 0% and specificity 100%. Both of these, would be extremely poor tests, but these simple examples demonstrate that the two measures are in some way complementary. (Hence the yin and yang.) We shall see later on another illustration of complementarity.
For COVID-19, the most commonly used tests are of two very different kinds - one attempts to tell whether the tested patient is currently infected, while the second detects antibodies against COVID-19. Tests in this second group do not detect whether the patient is currently infected, but only whether or not the patient has been infected in the past.
In the first group of tests, which detect current infection, there is again a division into two types. One, called a PCR test, looks for genetic fragments of the virus. The other tries to find bits of the virus' protein component. This last is called an antigen test, because it is this protein component that a body's immune system interacts with. (An antigen, according to Wikipedia, is a foreign substance invading the body and stimulating a response of the immune system.) Tests of the first type are generally more accurate than those of the second, but tests of the second type produce results much more rapidly - in minutes rather than hours or even days.
None of these tests is guaranteed to return correct results.
The first test taken by Governor DeWine was an antigen test, and his later tests were all PCR. In all these tests, samples were taken by nasal swabs. The antigen test was relatively new, and produced by the company Quidel. Initial versions were claimed to possess a sensitivity of around 80%, but more recent ones are claimed to have about 97% sensitivity, which is certainly comparable with PCR tests. They also claimed from the start a specificity of 100%.
The outcome of tests
What do these numbers mean? Given that Governor DeWine tested positive, what is the probability that he is infected with COVID-19?
One way to figure this out is to run some mental experiments. Suppose we give the tests to 1000 people chosen at random from a US population. What happens? It turns out that the answer to this depends on the infection level of the population, as we shall see. In other words, in order to carry out this experiment, I have to assume something about this level. Like many other things about COVID-19, this statistic is not known accurately, and in any case varies widely from place to place—perhaps, at this stage of the epidemic, a plausible range is between 1% and 15%. I'll try various guesses, using the values of sensitivity and specificity given by Quidel.
1. Suppose at first 5% of the population to be infected.
- In the sample of 1000, there will be around 50 who are currently infected.
- Because the sensitivity of the test is 97, of these about 48 will be labeled as positive, and the remaining 2 will not be correctly detected.
- But there remain 950 people in the sample who are not infected. For these it is the specificity that matters. I have assumed this to be 100%, which means that 100% of those who are not infected will be labeled as uninfected, and 0% will be found infected.
- Therefore, with these values of sensitivity and specificity, a nominal 48 will be found to be infected, and $850 + 2$ uninfected.
Wait a minute! Governor DeWine turned out ultimately not to be infected, but he was nonetheless found to be infected by the test. This contradicts the claim of 100% specificity! Something has gone wrong.
It is important to realize that the assigned values of sensitivity and specificity are somewhat theoretical, valid only if the test is applied in ideal conditions. Often in the literature these are called clinical data. But in the real world there are no ideal conditions, and the clinical specifications are not necessarily correct. Many errors are related to the initial sample taking, and indeed it is easy enough to imagine how a swab could miss crucial material. However, it is hard to see how an error could turn a sample without any indication of COVID-19 to one with such an indication. In any case, following the inevitable Murphy's Law, errors will certainly degrade performance.
2. This suggests trying out some slightly less favorable values for sensitivity and specificity, say 90% sensitivity and 95% specificity, but with the same 5% infection rate.
- In this case, 45 out of the true 50 infected will be caught, and 5 who will not be tagged.
- There will still be 950 who are not infected, but 5% = (100 - 95)% of these, i.e. about 48, will return positive.
- That makes another 48, and a total of 93 positive test results.
- In this experiment, Governor DeWine is one of 93, of whom 45 are infected, 48 not. Given the data in hand, it makes sense to say that the probability he is one of the infected is 45/93 = 0.49 or 49%. Definitely not to be ignored.
3. We might also try different guesses of the proportion of infection at large. Suppose it to be as low as 1%.
- Then of our 1000, 10 will be infected. Of these, 95% = 9 will test positive.
- In addition, there will be 990 who are not infected, and 5% or about 49 of these will test as positive, making a total of 58.
- Now the probability that the Governor is infected is 9/58 = 15%, much lower than before. So in this case, when the proportion of the overall population who are infected is rather small, the test is swamped by false positives.
4. Suppose the proportion of infected at large to be as high as 20%.
- Then of our 1000, 200 will be infected. Of these, 95% = 180 will test positive.
- In addition, there will be 800 who are not infected, and 5% or about 40 of these will test as positive, making a total of 220.
- Now the probability that the Governor is infected would be 180/220 = 82%, much higher than before. Looking at these three examples it seems that the test becomes more accurate as the overall probability of infection increases.
5. To get a better idea of how things go without rehearsing the same argument over and over, we need a formula. We can follow the reasoning in these calculations to find it. Let $a$ be the sensitivity (with $0 \le a \le 1$ instead of being measured in a percentage), and let $b$ be the specificity. Suppose the test is given to $N$ people, and suppose $P$ of them to be infected.
- Then $aP$ of these will be infected and test positive.
- Similarly, $(1-a)P$ will be infected but test negative.
- There are $N - P$ who are not infected, and of these the tests of $b(N-P)$ will return negative.
- That also means that the remainder of the $N-P$ uninfected people, or $(1-b)(N-P)$, will test positive (these are the false positives).
- That makes $aP + (1-b)(N-P)$ in total who test positive. Of these, the fraction who are infected, which we can interpret as the probability that a given person who tests positive is actually one of the infected is $$ { aP \over aP + (1 - b)(N-P) } $$
- We can express this formula in terms of probabilities instead of population sizes. The ratio $p = P/N$ is the proportion of infected in the general population. The ratio $q = (N-P)/N$ is the proportion of uninfected. Then the ratio in the formula above is $$ { ap \over ap + (1-b)q } $$
The advantage of the formula is that we don't have to consider each new value of $P/N$ on its own. Given $a$ and $b$, we can graph the formula as a function of the proportion $p = P/N$ of infected. For $a = 0.90$, $b = 0.95$ we get:
A good test is one for which the number of those who test positive is close to the number of those who are infected. The graph shows that this fails when the proportion of infected in the population at large is small. As I said earlier, the test is swamped by false positives.
Likewise, the proportion of infected who test negative (the potentially dangerous false negatives) is
$$ { (1-a)p \over (1 - a)p + bq } $$
And in a graph:
This time, the test is better if the graph lies low—if the number of infected who escape is small. The two graphs again illustrate that sensitivity and specificity are complementary. As the proportion infected in the population at large goes up, one part of the test improves and the other degrades.
The moral is this: sensitivity and specificity are intrinsic features of the tests, but interpreting them depends strongly on the environment.
Repeating the tests
As the case of Governor DeWine showed, the way to get around unsatisfactory test results is to test again.
To explain succinctly how this works, I first formulate things in a slightly abstract manner. Suppose we apply a test with sensitivity $a$ and specificity $b$ to a population with a proportion of $p$ infected and $q = 1-p$ uninfected. We can interpret these as probabilities: $p$ is the probability in the population at large of being infected, $q$ that of not being infected.
The test has the effect of dividing the population into two groups, those who test positive and those who test negative. Since the tests are not perfect, each of those again should be again partitioned into two smaller groups, the infected and the uninfected. Those who test positive have [infected:uninfected[] equal to $[ap : (1-b)q]$.
Those who test negative have [infected: uninfected] equal to $[(1-a)p:bq]$.
So the effect of the test is that we have divided the original population into two new populations, each of which also has both infected and infected. For those who tested positive, the new values of $p$ and $q$ are
$$ p_{+} = { ap \over ap + (1-b)q }, \quad q_{+} = { (1-b)q \over ap + (1-b)q } , $$
while for those who tested negative they are
$$ p_{-} = { (1-a)p \over (1-a)p + bq }, \quad q_{-} = { bq \over (1-a)p + bq }. $$
These are the new infection data we feed into any subsequent test, possibly with new $a$, $b$.
Now we can interpret Governor DeWine's experience. The first test was with the Quidel antigen test, say with $a = 0.90$ and $b = 0.95$. Suppose $p = 0.05$. Since the test was positive, the probability of the Governor being infected is therefore 0.49. But now he (and, in our imaginations, his cohort of those who tests were positive) is tested again, this time by the more accurate PCR test, with approximate accuracy $a = 0.80$ and $b = 0.99$. This produces a new probability $p = 0.16$ that he is infected, still not so good. But we repeat, getting successive values of $0.037$ and then $ 0.008$ that he is infected. The numbers are getting smaller, and the trend is plain. Governor DeWine has escaped (this time).
Estimating the number of infected
In effect, the test is a filter, dividing the original population into two smaller ones. One is an approximation to the set of infected, the other an approximation to the set of uninfected.
A second use of these tests is to try to figure out what proportion of the population is in fact infected. This is especially important with COVID-19, because many of the cases show no symptoms at all. The basic idea is pretty simple, and can be best explained by an example.
In fact, let's go back to an earlier example, with $N = 1000$, sensitivity $0.90$, specificity $0.95$, 150 infected. Of these, 177 test positive. We run the same test on these, and get 123 testing positive. Repeat: we get 109 positives.
What can we do with these numbers? The positives are comprised of true positives and false positives. The number of true positives is cut down by a factor of $0.90$ in each test, so inevitably the number of true positives is going to decrease as tests go on. But they decrease by a known ratio $a$! After one test, by a ratio $0.90$, after two tests, a ratio $0.90^{2} = 0.81$, after three by $0.90^{3} = 0.729$. Taking this into account, in order to find an approximation to the original number of infected we divide the number of positives by this ratio. We get the following table:
$$ \matrix { \hbox{ test number } & \hbox{ number of positives $N_{+}$ } & \hbox{ ratio $r$ } & N_{+}/r \cr 1 & 177 & 0.9 & 197 \cr 2 & 124 & 0.81 & 152 \cr 3 & 109 & 0.729 & 150 \cr } $$
Already, just running the test twice gives a pretty good guess for the original number infected.
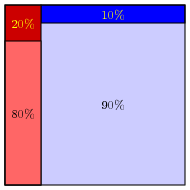
One of my colleagues pointed out to me a simple way to visualize what's going on. Suppose that we are looking at a population of 1000, 20% of whom are infected:
Then we run a test on it, with 20% sensitivity and 90% specificity.
The regions at the top are those whose tests are false.
Reading Further
- An earlier Feature Column about measles
- On the governor's tests:
- Popular articles
- Medical articles on testing. Many of these are somewhat technical, but still readable. And, to a mathematician, impressive as well as a bit intimidating.
Postscript
On the day I submitted this column to the American Mathematical Society for posting, a new antigen test was tentatively approved by the FDA. To be precise, the company Abbott Diagnostics was issued what is called an Emergency Use Authorization (EUA) for its product BinaxNOW. As the FDA web page says, there are now four such tests given this authorization (search for BinaxNOW on that page). The company claims clinical sensitivity 97.1% and specificity 98.5%, but time will tell whether it is in fact the "game-changer" it has been inevitably claimed to be.
You can find out more about this at:
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
Email Bill Casselman


 Bill Casselman
Bill Casselman