Mathematics and the Brain
Posted April 2007.
This is Mathematics Awareness Month, and this year's theme is Mathematics and the Brain...
Joe Malkevitch
York College (CUNY)
malkevitch at york.cuny.edu 
Introduction
The volume of a typical human brain is 1400 cm3 and its weight is about 1000 times that of a typical rat's brain. Mundane facts about brain data do little to give us insight into this amazing organ. What is there about the human brain that seems to make possible so many wondrous things that humans can accomplish: oral and written language, producing of art and music, and doing mathematics. Or is it really possible that dolphins have already resolved the status of the Riemann Hypothesis but we are unaware of it because we have found no way yet to communicate with them?
As so often seems to happen, at first glance there might not seem to be much to say about this topic. However, there are more facets to this subject than I can treat here or know enough about to say anything intelligent about them. I will merely try to provide you with a "wire" to connect mathematics and brain.
Imaging the Brain
One of the reasons the brain was a mystery for so long is that it is encased in the skull. Under ordinary circumstances one does not have easy access to seeing the brain. Being able to see into the human body took a big leap forward when Wilhelm Roentgen discovered x-rays. Shortly after his discovery of x-rays physicians were already using x-rays to see our bones. However, being encased by the skull, the brain, and other soft tissues were still unknown territory for physicians and physiologists. With contributions from science, engineering and mathematics, physicians have a growing array of imaging tools for seeing inside the skull. At first these brain imaging techniques involved 2-dimensional cross sections of the brain. Many of these techniques are identified with the field of tomography. The Greek word for a "cut" or "section" is "tomas." (Tomography has applications in fields other than medicine., for example, geology.) As the field of tomography has matured, it has been possible to generate three-dimensional medical imaging systems for the brain. These systems allow static views of the brain; increasingly it is also possible to make movies that show the dynamic behavior of the brain. The systems that are now available both to medical practitioners and researchers are:
* CT or CAT (Computed tomography or computed axial tomography)
* MRI (Magnetic Resonance Imaging)
*fMRI (Functional MRI)
* PET (Positron Emission Tomography)
* SPECT (Single Photon Emission Computed Tomography)
* DOT (Diffuse Optical Tomography)
"Vanilla" samples of some of these types of images are shown below:
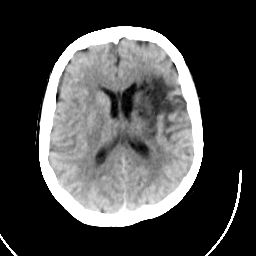 (A CT image of the brain. Image courtesy of Dr. Keith Johnson, Harvard Medical School.)
(A CT image of the brain. Image courtesy of Dr. Keith Johnson, Harvard Medical School.)
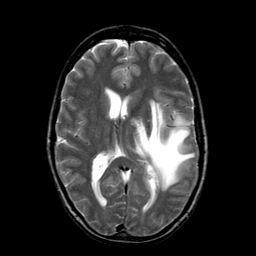 (An MRI image of the brain. Image courtesy of Dr. Keith Johnson, Harvard Medical School.)
(An MRI image of the brain. Image courtesy of Dr. Keith Johnson, Harvard Medical School.)
 (A SPECT/PET image of the brain. Image courtesy of Dr. Keith Johnson, Harvard Medical School.)
(A SPECT/PET image of the brain. Image courtesy of Dr. Keith Johnson, Harvard Medical School.)Images of the kind shown above have become part of the lexicon of our society. They show the brain using three different techniques that physicians have come to rely upon for insight and diagnosis.
The development of the CT-scans, computerized tomography, has proved to be one of the great leaps forward in diagnostic medicine and for medical research. It is a also a wonderful story of the interplay of pure mathematics, applicable mathematics, and computer science.
The story, amazingly enough, starts in Czechoslovakia. The mathematician Johnann Radon (1887-1956) was investigating the idea of reconstructing the value of a function at a point in a plane region by computing the sums (integral) of the values of this function along lines that intersected this domain. This work was published in German in 1917. Radon's work evolved into what is known today as the Radon Transform.

It is unclear if Radon saw a future for a medical revolution in his work but in any case, the engineering and the computer science to implement the implications of his ideas were in the future. Furthermore, his mathematical ideas also had to be amplified to make practical tomography a reality.
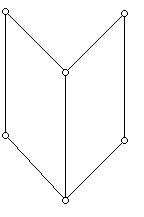
You can get the flavor of Radon's idea by consider the example below which involves a discrete analog of the question Radon investigated.
The vertices of the "square head" have unknown density, represented by x, y, z, and w. If one knows the sums of these unknown values along some (all) of the 6 line segments that are formed by the vertices of the square, can one reconstruct the unknown densities?

For example, using 4 of the 6 lines suppose we get the equations:
x + y = 8
w + z = 10
y + z = 13
w + y = 7.
Readers who know a little linear algebra may wish to see what happens for the general case here. Readers who know high school algebra should be able to determine that the equations above have a unique solution.
Usually four equations in four unknowns will give rise to a unique solution. However, it might be that these 6 equations are inconsistent and have no solution, or the solution might depend on which of the 4 out of 6 equations one selects. Problems of this kind belong to the emerging field of "discrete tomography." Such problems (the problem above involves the 2-dimensional cube), like Radon's original work, belong to the area of reconstruction of information from partial knowledge, or from "samples" of various kinds.
Radon showed that the unknown densities could be reconstructed from the "line integrals" that he was computing. Whether he or anyone realized the value of Radon's work for medical imaging at the time is unclear, but as noted previously, without significant computer power Radon's work could not be put to use immediately.
The story of CT scans picks up in more modern times with the work of Godfrey Hounsfield (1919-2004) and Allan Cormark (1924-1998). Hounsfield was an English electrical and mechanical engineer and Cormak was a South African physicist. The two men shared the Nobel Prize for Physiology and Medicine in 1979 for their work. However, in initially implementing the creation of a scanner in 1971 (based on earlier ideas) no use was made of Radon's work. Larry Shepp, a mathematician at Rutgers University, heard a talk by Hounsfield in which he described his new device. It emerged that Hounsfield was unaware of the possibility of using Radon's work in conjunction with his new machine, and Shepp became involved in developing computer code to improve the image quality for the new technology.
 (Larry Shepp)
(Larry Shepp)
As time has gone on, mathematicians have become increasingly involved with imaging technologies of many kinds.
The human visual system
One burgeoning area connecting mathematics and the brain is visual phenomena. Human visual information is processed by the brain and uses our amazing eyes. Mathematicians have been involved in a wide variety of problems involving vision:
* What is the geometry of our perceptual system?
* How does the brain process visual information?
It is well known that when humans look at (straight) railroad tracks they appear to converge in the distance. A wide range of scholars are trying to understand the mystery of visual perception. The way that the world looks to us was a challenge for artists who had to represent reality on canvas, and for philosophers who are trying to probe the relation between mind, physics, and perception. Artists met this challenge with a theory of perspective and mathematicians (some of them also artists) transformed the insights obtained concerning perspective into what today is known as projective geometry. In projective geometry, unlike Euclidean geometry, there are no parallel lines. However, this is not where the story ends. It has been suggested that the hyperbolic plane or other geometries might describe this system. The challenge of understanding perspective from a mathematical point of view and being able to use computers to serve the needs of artists, photographers, and architects has been a source of much research.
Illusions and impossible figures
One interesting connection between mathematics and the brain is the reaction many people have to symmetric patterns and patterns which are deceptive (visual illusions and impossible figures). Many individuals including mathematicians find symmetrical designs very appealing. For example, the works of M.C. Escher (1898-1972) hit a very sympathetic chord in the mathematics community.
Furthermore, these is a connection between Escher and interest in optical illusions and "impossible objects." This link is via Roger Penrose (1931-), the distinguished mathematician and physicist, whose impossible triangle has inspired a large number of artistic efforts, including those of Escher, as well as mathematical and computer vision investigations.
However, it not as widely known as it should be that Penrose was not the first to create such images, though his version of the illusion is particularly appealing.
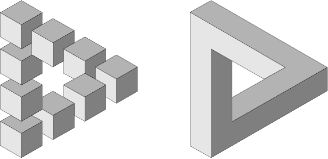 (Courtesy of Eric Weisstein. Weisstein, Eric W. "Penrose Triangle." From MathWorld--A Wolfram Web Resource.
(Courtesy of Eric Weisstein. Weisstein, Eric W. "Penrose Triangle." From MathWorld--A Wolfram Web Resource.
http://mathworld.wolfram.com/PenroseTriangle.html)
In the diagram above the version due to Roger Penrose is shown on the right but the illustration on the left shows a version of this object first created in 1934 by the Swedish artist Oscar Reutsvärd. Reutsvärd's work has been commemorated by a Swedish stamp and his version of the impossible triangle is but one of many such illusions that he created. It turns out that another aspect of "impossible figures" is making real objects which look exactly like impossible ones. There is more to illusions than meets the eye or the brain.
Illusions open up a window to explore the nature of our visual system, the way the brain processes visual information, and the geometry of our visual perception system. Experts in computer vision, a subject which includes effective ways of manipulating images by computers as well as developing software to carry out various pattern recognition problems, are also interested in visual illusions. Applications of work in this area might range from more effective face recognition software to scene recognition capability for software. Here is a small sample of visual illustions which show some the range of phenomena that might be explored concerning why the brain is "fooled" and which can perhaps be modeled using mathematics.
Other mathematical windows on the brain
The small sample of ways that mathematics interacts with our knowledge of the human brain barely hints at the myriad of interfaces of these two subjects. What follows is just an additional sampler of ways that mathematics is interacting with and providing a valuable tool for attempts to understand the brain.
* Neuronal organization and transmission of signals (nerve conduction) between the brain and other parts of our nervous system
* The use of dynamical systems in an attempt to understand epilepsy and to be able to try to predict the start of seizures
* Modeling various aspects of the brain using mathematics which tries to understand how "oscillators" coordinate their firings under various interaction assumptions
* Using new ideas about flattening complicated surfaces (like the brain) to understand how to map different parts of the brain to specific brain functions
* Using data mining and other tools to understand the implications of an increasing wealth of DNA and genomic information for brain chemistry
Mathematical ability
To the best of our knowledge humans are the only species that does mathematics. Attempts to verify that other animals (plants?) can "do" mathematics have so far not encouraged the belief that any mathematics is being produced by other species. The famous story of "clever Hans," a horse whose master had convinced himself that Hans could do mathematics turned out to be not a case of a horse with mathematical talent but a human master who was sending signals to the horse without realizing he was doing this. What is unique about the human brain that makes this doing mathematics possible? Brain imaging techniques are being used to chart the differences in how humans might do calculations, visualize a polyhderon, try to prove a theorem, or brain storm a problem in number theory. What are the ways that having a "good memory" makes mathematics easier? Many mathematicians describe themselves as having a good memory. What can be said is that mathematicians are using their brains and mathematics to further mathematics' domains and to get further insight into how mathematics gives insight into brains!
References
Anderson, S., and D. Burr, Spatial and temporal selectivity of the human motion detection system, Vision Research 25 (1985) 1147-1154.
Anger, B., and C. Portenier, Radon Integrals, Birkhauser, Boston, 1992.
Babloyantz, A., and C. Lourenco, Brain chaos and computation. Int J Neural Syst 7 (1996) 461-71.
Beigler, R. and A. McGregor, and S. Healy, How do animals "do" geometry?, Animal Behavior 57 (1999) F4-F8.
Blakemore, C., and F. Campbell, On the existence of neurones in the human visual system selectively sensitive to the orientation and size of retinal images, J. of Physiology (1969) 203-237.
Cabeza, R., and A. Kingstone, (eds.), Handbook of Functional Neuroimaging Cognition, second edition, MIT Press, Cambridge, 2006.
Chomsky, N., Language and Mind, Harcourt Brace Jovanovich, New York, 1972.
Cowan, T., The theory of braids and the analysis of impossible figures, J. Math. Psychology 11 (1974) 190-212.
Cowan, T., Turning a Penrose triangle inside out, J. Math. Psychology 26 (1982) 252-262.
Cowan, T., and R. Pringle, An investigation of the cues responsible for figure impossibility, J. of Experimental Psychology: Human Performance and Perception, 4 (1978) 112-120.
Deans, S., The Radon Transform and Some of Its Applications, Wiley, New York, 1968.
De Cruz, H., Towards a Darwinian approach to Mathematics, Foundations of Science, 11 (2006) 157-196.
Dehene, S., Cerebral bases of number processing and calculation, In M. Gazzaniga (ed.), The New Cognitive Neurosciences, (Second Edition), MIT Press, Cambridge, 2000, p. 987-998.
Derchansky, M., Examining the Epileptic Brain with Nonlinear Mathematics (Preprint).
De Valois, R., and K. De Valois, Spatial Vision, Oxford Press, Oxford, 1988.
Esser, P. (ed.), Emission Computed Tomography: Current Trends, Society of Nuclear Medicine, New York, 1983.
Gardner, R., Geometric Tomograpy, Cambridge U. Press, New York, 1995.
Gindikin, S. (ed.), Applied Problems of Radon Transforms, American Mathematical Society, Providence, 1994.
Greenfield, S., The Human Brain: A Guided Tour, Phoenix, London, 1998.
Griffin, D., Animal Minds. Beyond Cognition to Consciousness, U. of Chicago Press, Chicago, 2001.
Grünbaum, B. and G. Shephard, Tilings and Patterns, W.H. Freeman, New York, 1987.
Helgason, S., The Radon Transform, Birkhauser, Boston, 1980.
Herman, G., Image Reconstruction from Projections: The Fundamentals of Computerized Tomography, New York, Academic Press, 1980.
Herman, G. and A. Kuba (eds.), Discrete Tomography: Foundations, Algorithms, and Applications, Birkhauser, Boston, 1999.
Hoffman, W., Subjective geometry and geometric psychology, Mathematical Modeling 1 (1980) 349-367.
Hong, W., A. Yang, K. Huang, Y. Ma, On symmetry and multiple-view geometry: Structure, pose, calibration from a single image, International J. of Computer Vision 60 (2004) 241-265.
Hoppensteadt, F., An Introduction to the Mathematics of Neurons, Cambridge U. Press, New York, 1986.
Huffman, D., Impossible objects as nonsense sentences. In B. Meltzer and D.
Lorenceau, J., Geometry and the visual brain, J. of Physiology, 97 (2003) 99-103.
Michie (eds.), Machine Intelligence, Volume 6, Halstead, New York, 1971.
Lehnertz, K., Non-linear time series analysis of intracranial EEG recordings in patients with epilepsy--an overview., Int J Psychophysiol 1999;34(1):45-52
Lehnetz, K., and C. Elger, Can epileptic seizures be predicted? Evidence from nonlinear time series analysis of brain electrical activity, Phys Rev Lett 1998;80:5019-26.
Le Van Quyen, M., Anticipating epileptic seizures: from mathematics to clinical applications, Comptes Rendus Biologies 328 (2005) 187-198.
Li, S., and D. Mital, E. Teoh, H. Wang, (eds.), Recent Developments in Computer Vision, Springer, Berlin, 1995.
Ma., Y., J. Kosecka, S. Soatto, S. Sastry, An Invitation to #-D Vision: From Images to Geometric Models, Springer-Verlag, New York, 2003.
Penrose, L., and R. Penrose, Impossible objects: A special type of illusion, British J. of Psychology, 49 (1958) 31-33.
Plamer, S., Vision Science: Photons to Phenomenology, MIT Press, Cambridge, 1999.
Rann, A. and A. Katsevich, The Radon Transform and Local Tomography, CRC, Boca Raton, 1996.
Shepp, L., (ed.), Computed Tomography, Volume 27, Proceedings of Symposia in Applied Mathematics, American Mathematical Society, Providence, 1983.
Shepp, L., and J. Kruskal, Computerized tomography: The new medical X-ray technology, Amer. Math. Monthly 85 (1978) 420-439.
Starkey, P., and R. Cooper, Perception of Numbers by Human Infants, Science 210 (1980) 1033-35.
Sugihara, K., Machine Interpretation of Line Drawings, MIT Press, Cambridge U. Press,
Wynn, K., Addition and subtraction by human infants, Nature 358 (1992) 749-750.
Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet can be used to get additional bibliographic information and reviews of some of these materials. Some of the items above can be accessed via the ACM Portal, which also provides bibliographic services.
Joe Malkevitch
York College (CUNY)
malkevitch at york.cuny.edu