Diagonals: Part I
4. Art gallery problems
In 1973 the geometer and topologist Victor Klee (University of Washington) posed an innocuous-looking problem.

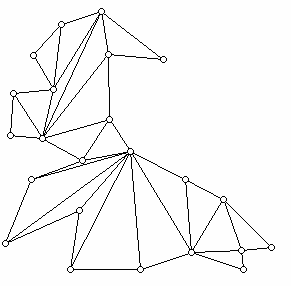
In the language that has come to be used for the problem, he was interested in the number of points, sometimes called guards, needed to "guard" a plane simple polygon. Think of a plane simple polygon as the floor plan of an art gallery or museum and the guards as being point sensors which send out a beam similar to those used in home alarm systems. The goal of the guards is to make sure that any point where an intruder might be would be "visible" to the guards. What are the capabilities of a "guard" and what is the concept behind "guarding"? The intuitive idea has to do with what points are visible via the line of sight in a simple polygon. If g is a point of a polygon P, either in the interior of the polygon or on its boundary, a point x (in the interior or on the boundary of P) is said to be visible fromg if no part of the segment gx lies in the exterior of P. Note that ifx is visible from g, then g is visible from x. This definition means that if an edge or vertex of a polygon P is on the line of sight between two points g and x of P, we still say that they are visible from each other. Thus, from any point g of a polygon P we can determine the set of all points of P visible from g. This set of points is a polygon and is known as the visibility polygon ofg. In the diagram below, all of the polygon is visible from v while only the red region is the visibility polygon from u.
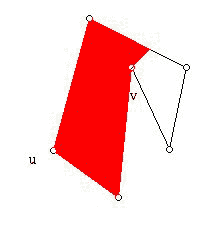
Note that the line segment beyond v along the line joining u and v up to the boundary of the polygon is part of the visibility region. A guard for the interior of a simple polygon can be placed at a vertex (usually called a vertex guard), on an edge, or in the interior. Intriguingly, for some types of guarding problems (which may involve the interior or the exterior of a polygon, and have special conditions on the type of polygon to be guarded), the number of guards needed when guards are required to be vertex guards is the same as for other types of guards. However, in other problems what can be achieved with vertex guards is vastly different from the general case. To help understand the issue, convince yourself that no vertex guard can see all of the interior of the polygon below, while there is a point in the interior of the polygon from which all of the interior can be seen.
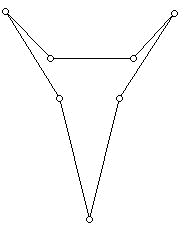
Figure 2
Instead of using the language of guards and visibility, sometimes problems of this kind use the language of lamps and illumination. Imagine a lamp that sends out a beam which illuminates what it "passes over" or hits. The idea is to use as few lamps as possible to achieve some illumination goal. Whereas the earliest problems involving guards and art galleries implicitly thought of the region to be guarded as being the interior of some set, the illumination problems thought of a collection of sets with some special characteristics (e.g. rectangles or segments) and one wanted to illuminate the "outside" or boundaries of the sets by placing lamps exterior to the objects being illuminated. For physically realistic problems neither guards nor lamps can send a beam throughout the full 360 degrees around them, so one can make assumptions about the angle in which the beam or illumination must be restricted. Here, we will consider guards able to see a full 360 degrees. Victor Klee and Laszlo Fejes-Tóth raised problems couched in the illumination perspective.
The diagrams of the two simple plane polygons below will help you understand the issues involved in investigating the number of guards needed to guard a simple polygon. Each polygon has 8 sides but clearly the polygon on the left needs only one vertex guard. In contrast, a convoluted polygon such as the one on the right will, in this case, need more than one guard.
Vasek Chvátal (pictured below), who first answered Klee's question, no doubt experimented with determining the minimum number of guards a particular polygon requires.
When contemplating finding the minimum number of guards for a polygon, quickly one notes that some many-sided polygons require only one guard: A convex polygon, regardless of the number of sides, requires only one guard, as do many non-convex polygons. It's a nice "exercise" to find the smallest number of sides that a polygon must have which requires it to have at least 2 guards. The answer to this exercise is 6. For example, the polygon below requires 2 guards.
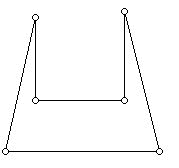
Armed with this example, it's easy to see how one can add three more sides to the polygon above and now require 3 guards. Chvátal realized that for a particular convoluted polygon Q with n sides it might be quite difficult to determine the exact number of guards needed to guard Q. In fact, it has been shown that it is unlikely that there is a polynomial time algorithm to find the minimum number of guards for a particular polygon. However, for a general polygon with n sides it always seemed that 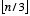 guards sufficed (where
guards sufficed (where 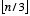 means the largest integer less than or equal to n/3). The family of 3n-sided polygons which generalizes the hexagon above shows that sometimes one needs n guards for a 3n-sided polygon. Based on the family of examples above, and Chvátal's experiments, the following conjecture emerges:
means the largest integer less than or equal to n/3). The family of 3n-sided polygons which generalizes the hexagon above shows that sometimes one needs n guards for a 3n-sided polygon. Based on the family of examples above, and Chvátal's experiments, the following conjecture emerges:
Conjecture: For a simple plane polygon with n sides, 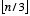 guards are sometimes necessary and always suffice to guard the polygon. Furthermore, these guards can always be placed at vertices of the polygon.
guards are sometimes necessary and always suffice to guard the polygon. Furthermore, these guards can always be placed at vertices of the polygon.
Chvátal (now at Rutgers University) gave the first proof of this conjecture, now often referred to as the Art Gallery Theorem. His proof was elementary and a very nice piece of mathematics, which proved useful in a variety of problems. However, it remained for Steve Fisk (Bowdoin College) to find a "book proof." This phrase refers to the metaphor of Paul Erdős that God keeps a book of the most elegant theorems and their proofs. Fisk's proof consists of showing that every simple triangulated polygon can have its vertices colored with exactly 3 colors. In fact, once one colors any triangle, the colors for the remaining vertices of the triangulation are completely determined. A rigorous proof that a 3-coloring of the vertices is possible follows from the the fact that by locating an ear and removing it, one can 3-color a smaller triangulation, and when the removed ear is restored, since it abuts the smaller triangulation on an edge, there is a third color available to be able to color the removed vertex. Rather than give Fisk's proof in a general case, let us use the following sequence of diagrams to show how the proof works for a specific case. The first diagram shows a simple polygon, albeit a rather convoluted one.
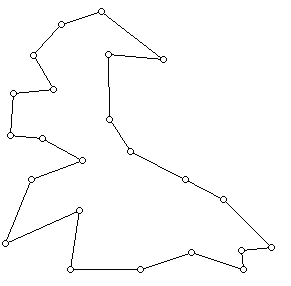
This polygon can be triangulated in a variety of ways, one of which is shown below:
The vertices of this triangulation are now 3-colored with red, blue, and green. Since each triangle is colored with each of the 3 colors, if we place guards at all the red vertices, or all the green vertices, or all the blue vertices, we will have the whole polygon guarded. Clearly, it makes sense to put the guards at the set of vertices of the three different colors which has the minimum size! This will always give rise to a coloring with no more than 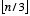 colors.
colors.
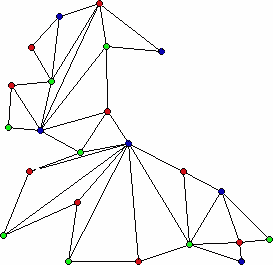
If we place guards at the 6 blue vertices, the whole polygon will be successfully guarded. However, you should be able to convince yourself that in fact only 3 guards are required. Fisk's approach shows that no more than 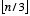 will ever be needed but for a particular polygon it does not say what the minimum number of guards would be. In fact, if you look back at Figure 2 you will find that no single guard located at a vertex will see all of the polygon, while there is an interior point where a guard can be placed from which all of the polygon is visible.
will ever be needed but for a particular polygon it does not say what the minimum number of guards would be. In fact, if you look back at Figure 2 you will find that no single guard located at a vertex will see all of the polygon, while there is an interior point where a guard can be placed from which all of the polygon is visible.
- Introduction
- What is a diagonal?
- Triangulations and ears
- Art gallery theorems
- Where do new problems come from?
- References









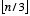 guards sufficed (where
guards sufficed (where