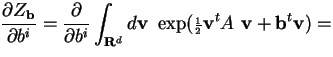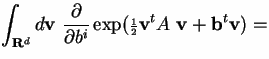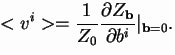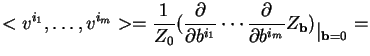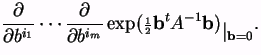Feature Column from the AMS

Finite-dimensional Feynman Diagrams

3. m-point functions

For any choice of m(not necessarily different) indices i₁, ... , i_mbetween 1 and d,define the m-point function $<v^{i_1}, \dots , v^{i_m}>$ as follows:

$\displaystyle <v^{i_1} ,\dots , v^{i_m}> = \frac{1}{Z_0}\int_{{\bf R}^d} d{\bf v} ~~\exp({\scriptstyle\frac{ 1}{ 2}}{\bf v}^tA~{\bf v})v^{i_1},\dots , v^{i_m}.$

The m-point functions are a step towards the ultimate aim of our calculation.They enter at this moment because they can be calculatedby repeated differentiation of Z_b

For example, note that

$\displaystyle \frac{\partial Z_{\bf b}}{\partial b^i} = \frac{\partial}{\partia......f v} ~~\exp({\scriptstyle\frac{ 1}{ 2}}{\bf v}^tA~{\bf v} + {\bf b}^t{\bf v}) =$

$\displaystyle \int_{{\bf R}^d} d{\bf v} ~~ \frac{\partial}{\partial b^i}\exp({\scriptstyle\frac{ 1}{ 2}}{\bf v}^tA~{\bf v} + {\bf b}^t{\bf v}) =$

$\displaystyle \int_{{\bf R}^d} d{\bf v} ~~ \exp({\scriptstyle\frac{ 1}{ 2}}{\bf v}^tA~{\bf v} + {\bf b}^t{\bf v}) v^i.$

So the 1-point function <vⁱ>is given by

$\displaystyle <v^i> = \frac{1}{Z_0} \frac{\partial Z_{\bf b}}{\partial b^i}\vert _{{\bf b} =0}.$

Similarly the m-point function $<v^{i_1}, \dots , v^{i_m}>$ is given by

$\displaystyle <v^{i_1} ,\dots , v^{i_m}> =\frac{1}{Z_0} (\frac{\partial}{\parti......\frac{\partial}{\partial b^{i_m}}Z_{\bf b})_{\textstyle \vert _{{\bf b} =0}} =$

$\displaystyle \frac{\partial}{\partial b^{i_1}}\cdots \frac{\partial}{\partial ......criptstyle\frac{1}{2}}{\bf b}^tA^{-1}{\bf b})_{\textstyle \vert _{{\bf b} =0}}.$

Welcome to the
Feature Column!

These web essays are designed for those who have already discovered the joys of mathematics as well as for those who may be uncomfortable with mathematics.
Read more . . .

Search Feature Column

Feature Column at a glance