Where do the "best" rational approximations come from?
The "best" rational approximations, as well as most of the theory of rational approximation, arise from continued fraction expansions.
A continued fraction expansion for a positive number x is a sequence of positive integers a1,a2,a3, ... such that x is the limit of the rational numbers:
$c_1 = a_1$
$c_2 = a_1 + \frac{1}{a_2}$
$c_3 = a_1 + \frac{1}{a_2 + \frac{1}{a_3}}$
$c_4 = a_1 + \frac{1}{a_2 + \frac{1}{a_3 + \frac{1}{a_4}}}$
$c_5 = \ldots$
The numbers c1, c2, etc are called the convergents of x. They are important in this context because the best rational approximations to an irrational number are always found among its convergents.
Any rational number p/q which approximates x to within 1/(2q2) must be one of the convergents of x.
In terms of our table, this means that any rational approximation with E/M < 1.118.. must be a convergent.
Calculating a continued fraction expansion
- From the decimal expansion. If we know the number well enough, for example to enough decimal places, we can calculate its continued fraction expansion as we show here with x =
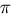 = 3.14159265359...
= 3.14159265359...
The point is to make c1, c2, c3, etc. alternately smaller and larger than x by choosing the largest possible a1, a2, a3, etc.
- a1 is the integer part, here 3. This is the largest integer which makes c1 less than
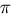 .
.
- With a1 = 3, a2 is the largest integer which makes c2 greater than
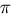 .
.
8 is too large because 3 + 1/8 = 3.125... < 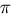 ,
,
but 7 makes it since 3 + 1/7 = 3.1428.. > 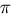 .
.
So a2 = 7, and c2 = 3 + 1/7 = 22/7.
- With a1 = 3 and a2 = 7, a3 is the largest integer which makes c3 less than
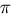 .
.
16 is too large because 3 + 1/(7+1/16) = 3.14159292... > 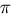 ,
,
but 15 works since 3+1/(7+1/15) = 3.1415094... < 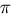 .
.
So a3 = 15, and c3 = 3+1/(7+1/15) = 333/106.
- Continue, alternating "greater" and "less." You should find a4 = 1 and a5 = 292. More a's will require more decimal places.
- If the number is a root of a quadratic equation ax2 - bx - c = 0 with b strictly positive, and a = c = 1, the equation yields an algorithm for generating the continued fraction expansion.
 itself does not work, but x=1+
itself does not work, but x=1+ is a root of x2-2x-1=0. The equation can be rewritten as x=2+1/x. Substituting the right hand side into itself gives x = 2+1/(2+1/x), and then x = 2+1/(2+1/(2+1/x)) etc. Since
is a root of x2-2x-1=0. The equation can be rewritten as x=2+1/x. Substituting the right hand side into itself gives x = 2+1/(2+1/x), and then x = 2+1/(2+1/(2+1/x)) etc. Since  = (1+
= (1+ ) - 1, the procedure yields for
) - 1, the procedure yields for  the continued fraction expansion:
the continued fraction expansion:
$1 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2 + \ldots}}}}$
and the convergents for  are c1= 1, c2= 3/2, c3 = 7/5, c4 = 17/12, c5 = 41/29, c6 = 99/70, c7 = 239/169, ...
are c1= 1, c2= 3/2, c3 = 7/5, c4 = 17/12, c5 = 41/29, c6 = 99/70, c7 = 239/169, ...
On to next irrational page.
Back to previous irrational page.
Back to first irrational page.
Welcome to the
Feature Column!
These web essays are designed for those who have already discovered the joys of mathematics as well as for those who may be uncomfortable with mathematics.
Read more . . .
Feature Column at a glance



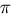 = 3.14159265359...
= 3.14159265359...
 itself does not work, but x=1+
itself does not work, but x=1+