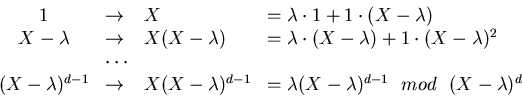metonymy5 Metonymy and Metaphor in Mathematics
5. Metaphors from modern mathematics:
II. The Jordan normal form and the structure of abelian groups
Two  matrices A and B are similar if there is an invertible
matrices A and B are similar if there is an invertible  matrix S such that B=S-1AS. This means that A and B are ``doing the same thing'' but seen with respect to two different sets of basis vectors.
matrix S such that B=S-1AS. This means that A and B are ``doing the same thing'' but seen with respect to two different sets of basis vectors.
Any  matrix A with complex entries is similar to a matrix in Jordan normal form. This is a matrix of the form
matrix A with complex entries is similar to a matrix in Jordan normal form. This is a matrix of the form
where 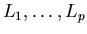 are square blocks of various sizes adding up to n, arranged along the diagonal, and the 0s represent appropriate blocks of zeroes. Furthermore each Li has the form
are square blocks of various sizes adding up to n, arranged along the diagonal, and the 0s represent appropriate blocks of zeroes. Furthermore each Li has the form
for some complex number 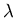 .
.
The metaphier. The structure theorem for finite abelian groups says that a finite abelian G is isomorphic to a direct sum of cyclic groups 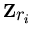 , where ri is a power of a prime, and that this decomposition is unique up to ordering. For example, an abelian group of order 12 must be isomorphic to either
, where ri is a power of a prime, and that this decomposition is unique up to ordering. For example, an abelian group of order 12 must be isomorphic to either 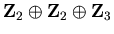 or
or 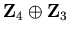 . There are no other possibilities. This generalizes to a structure theorem for modules over a principal ideal domain.
. There are no other possibilities. This generalizes to a structure theorem for modules over a principal ideal domain. 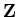 and the ring
and the ring ![${\bf C}[X]$](/featurecolumn/images/met5img10.gif) of complex-valued polynomials are both p.i.d.s; an abelian group is naturally a
of complex-valued polynomials are both p.i.d.s; an abelian group is naturally a 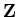 -module, with
-module, with 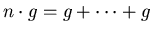 (n times).
(n times).
The metaphor. Use A to make 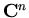 into a
into a ![${\bf C}[X]$](/featurecolumn/images/met5img10.gif) -module by letting
-module by letting  so
so  , etc. The analogue of
, etc. The analogue of 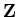 mod the multiples of ri (a prime power) is
mod the multiples of ri (a prime power) is ![${\bf C}[X]$](/featurecolumn/images/met5img10.gif) mod the multiples of
mod the multiples of 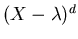 , since in
, since in ![${\bf C}[X]$](/featurecolumn/images/met5img10.gif) the irreducible polynomials are linear.
the irreducible polynomials are linear.
By the structure theorem, 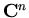 splits up into subspaces
splits up into subspaces
and restricted to Ei the module structure is the same as the action of ![${\bf C}[X]$](/featurecolumn/images/met5img10.gif) on
on ![${\bf C}[X]/((X-\lambda)^d)$](/featurecolumn/images/met5img17.gif) , for some complex
, for some complex 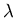 . A basis for the quotient is
. A basis for the quotient is
With respect to this basis the matrix of A, which corresponds to multiplication by X, comes out as follows:
giving exactly the block Li described above.
(For more details see a text like Hartley and Hawkes, Rings, Modules and Linear Algebra,Chapman & Hall, London, New York, 1970 or Serge Lang, Algebra, Addison-Wesley 1971.)
Welcome to the
Feature Column!
These web essays are designed for those who have already discovered the joys of mathematics as well as for those who may be uncomfortable with mathematics.
Read more . . .
Feature Column at a glance