Penrose Tiles Talk Across Miles
Posted August 2005.
The inflated tiling is itself a tiling by thick and thinrhombs and, as such, it has an inflated tiling as well. This creates,from a single tiling, an infinite hierarchy of tilings in which eachtiling is the inflated tiling of its predecessor.
David Austin
Grand Valley State University
david at merganser.math.gvsu.edu 
Introduction: Tilings
Tilings, like the one below, show up in many places in the world around us, from the tiles on our kitchen floors to the bees' honeycombs. They generally have a pleasing, even fascinating, quality, their regularity often expressing some natural harmony.

Most of us are aware that tiling the plane with a single type of regular polygonal tile is possible only with triangles, squares and hexagons.



Johannes Kepler, in his 1619 work Harmonice Mundi, created the first list of all the Archimedean tilings, tilings that can be created from sets of regular polygons. Besides the three tilings above, he found eight more:
These tilings possess many symmetries. For example, looking at the tiling below, notice how the region inside each parallelogram is the same. This means that we could reconstruct the tiling from a single parallelogram by placing copies of the parallelogram side by side. In this way, the parallelogram represents a fundamental unit of the tiling, and we say that the tiling is periodic.

Another way to express this fact is to say that there are translational symmetries of the tiling. That is, the entire plane could be shifted in the direction and by the length of one side of a parallelogram and the tiling would lay down on top of itself.
There are rotational symmetries as well. For instance, there is 3-fold rotational symmetry about the center of any of the triangles, 4-fold symmetry about the centers of the squares and 6-fold symmetry about the center of the hexagons. This shows that periodic tilings can have 3-fold, 4-fold and 6-fold symmetry. A short argument shows, however, that a tiling with translational symmetry can never have 5-fold rotational symmetry.
It is natural to ask whether tilings must always be built by periodically repeating fundamental units or whether there are more "disorderly" tilings that do not exhibit periodicicity. Indeed, it is not difficult to find nonperiodic tilings, an example of which appears below.

Notice, however, that the tiles may be rearranged to create a periodic tiling.

In the 1960's, Hao Wang, motivated by a question in symbolic logic, asked whether there was a set of tiles whose tilings are all nonperiodic. That is, any tiling of the plane created from such a set of tiles must have no translational symmetry. Within a few years, Robert Berger found a set of 20,426 tiles with this property.
In the early 1970's, Roger Penrose and Robert Ammann independently found sets of tiles with considerably fewer tiles. The first set of tiles Penrose found had six tiles and could tile the plane as shown here.

In this figure, it appears that there are only four types of tiles. However, as will be explained momentarily, differently colored pentagons will be considered to be different types of tiles.

Notice also that there is five-fold rotational symmetry, about the center of the lightened pentagon, reflecting the nonperiodicity of the tiling. In fact, any tiling created using this set of tiles must be nonperiodic.
Penrose later found sets of tiles--one consisting of "kites and darts" (top image below), the other of thick and thin rhombs (bottom image below)--with only two types of tiles. Both sets of tiles only tile the plane nonperiodically.


The three sets of Penrose tiles exhibit an underlying unity: Given a tiling using one of the sets, we can form a tiling using either of the other sets.
Matching Rules
Penrose's tiles have some additional structure that is not shown in the figures above. For the sake of convenience, we will restrict our attention to the rhombs.

In fact, Penrose's rhombs could more faithfully be drawn like this:

Notice that the deformations on the sides restrict the way in which tiles may be laid next to each other. A more commonly used method to represent these restrictions is to decorate the edges of the rhombs with arrows and require that the arrows, both the number and direction, on edges of adjacent rhombs agree.
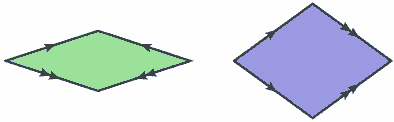
These requirements are generally referred to as matching rules; the tiling with rhombs shown above satisfies these rules. Earlier, I mentioned that there were three different types of pentagons in Penrose's original set of tiles. These different types correspond to three different matching rules along the edges of the pentagons.
Another method to represent the matching rules involves decorating the rhombs themselves
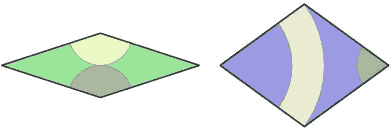
and requiring that the decorations on adjacent rhombs fit together consistently.

The decorations make patterns appear more clearly. For instance, notice that there are small patches of tiles that seem to occur several times throughout the tiling. Examining a larger portion of the tiling, however, will convince you that there is no apparent translational symmetry. I shall have more to say about this later. Also, while this tiling does not have five-fold symmetry, there are regions, sometimes even quite large, that do have such symmetry.
As a final means of representing the matching rules, Ammann discovered that the rhombs could be decorated with what are now called Ammann bars.

The matching rules are enforced by requiring that the bars on adjacent tiles fit together to form five families of parallel lines.

Constructing tilings
Because Penrose rhombs cannot tile the plane periodically, there can be no fundamental unit to serve as a basis for a tiling. This makes constructing Penrose tilings a challenge.
If you would like to construct a tiling of the plane using Penrose rhombs--that is, if you wanted to fill up the entire plane with tiles leaving no gaps--you might first try to lay down some tiles and see if there is an obvious way to continue. Here is a Java program that will help you experiment.
You will most likely find that you eventually reach a configuration that cannot be extended. For example, the figures below show two patches of tiles put together using the matching rules. It is not possible, however, to add tiles to cover the red dots.
Inflation
This example shows that it is not possible to create tilings using only the matching rules. Some other consideration must be made. In this column in December, I shall explain a few ways to construct Penrose tilings; we will see then that the number of different tilings is uncountably infinite. I would, however, like to explain the central idea behind this fact and indeed much of what we know about Penrose tilings.
In this discussion, it will be helpful to break the rhombs apart into half-rhombs:

Focusing on an arrowed side of a half-rhomb, we see that there are only two possibilities for adjacent half-rhombs. This produces rather severe restrictions on how half-rhombs may be placed. More specifically, checking the possibilities leads to the following:
| In a Penrose tiling, every half-rhomb uniquely fits into one of the following patches. |
 |
 |
The important point to note here is that these patches are themselves thick and thin rhombs, whose linear dimensions have been scaled by the golden ratio  If we now look at a tiling and superimpose the scaled rhombs formed by grouping half-rhombs, we see that another tiling is created.
If we now look at a tiling and superimpose the scaled rhombs formed by grouping half-rhombs, we see that another tiling is created.

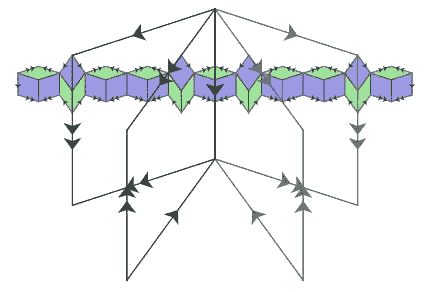
We call this tiling the inflated tiling of the original. In fact, the inflated tiling is itself a tiling by thick and thin rhombs (one can check that the matching rules are satisfied) and, as such, it has an inflated tiling as well. This creates, from a single tiling, an infinite hierarchy of tilings in which each tiling is the inflated tiling of its predecessor. The figure below illustrates this hierarchy in a tiling formed from Penrose's original set of tiles. Here, the original tiling is formed by the colored tiles. The thin black lines indicate the inflated tiling of the original tiling. The thicker black lines indicate the inflated tiling of the inflated tiling and so on. Notice that as we ascend from one level to the next in the inflation hierarchy, the tiles are scaled by 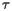 , and so the size of the tiles grows exponentially.
, and so the size of the tiles grows exponentially.

Here is a Java program that moves through the inflation hierarchy for a tiling by rhombs.
The inflation hierarchy explains why a Penrose tiling can have no translational symmetry. Since the inflated tiling is unique, any translational symmetry of a tiling must be a symmetry of its inflated tiling, and therefore every tiling in the inflation hierarchy. However, if we move up far enough in the inflation hierarchy, the size of the tiles is eventually much larger than the length of the translation. It is therefore impossible for the translation to be a symmetry of that inflated tiling, and so the translation cannot be a symmetry of the original tiling.
A second fact implied by the inflation hierarchy is also curious. We noticed earlier that there were small patches of tiles that seemed to show up repeatedly in a tiling. In fact, any finite patch that we choose in a tiling will lie inside a single inflated tile if we continue moving far enough up in the inflation hierarchy. This means that anywhere that tile occurs at that level in the hierarchy, our original patch must also occur in the original tiling. Therefore, the patch will occur infinitely often in the original tiling and, in fact, in every other tiling as well. The figure above illustrates this fact.
Taken together, these two facts speak to the remarkable nature of Penrose tilings. There is never a translation that preserves the entire tiling, and so there is no fundamental unit that generates the tiling. Any finite patch, however, appears infinitely often in the tiling.
The inflation hierarchy can also help us construct tilings. Remember that if we place tiles using only the matching rules, we often create patches that cannot be extended. We may avoid this fate, however, if in addition to the matching rules, we also require that the rhombs in the patch we have constructed may be grouped so as to form an extensible inflated patch. Here is a Java program that allows you to add a tile only when the resulting patch is consistent with some extensible inflated patch.
Crystallography
Though Penrose tilings grew out of recreational mathematics, they were soon pressed into service to explain a new phenomenon in crystallography, the study of solids that are "ordered" at the microscopic level. Historically, it was assumed that this order was created by the periodic repetition of a fundamental unit. Indeed, the advent of X-ray diffraction seemed to confirm this assumption as all observations made over the course of 70 years were consistent with it. In particular, diffraction patterns with 5-fold rotational symmetry were never observed, a fact that was seen to validate the assumption that the order in crystals arose from a periodic internal structure.
In 1982, Schechtman and his associates rapidly cooled an aluminum-manganese sample and observed that the alloy produced a diffraction pattern with 5-fold rotational symmetry. Though this pattern could not be formed by a periodic crystal, the diffraction pattern itself clearly reflected some type of orderliness in the alloy.
Following Schechtman's discovery, many more examples of this phenomenon were observed. After considerable debate, it is now accepted that these materials, quasicrystals as they are called, arise as three-dimensional analogues of Penrose tilings. Rather than periodicity, the inflation hierarchy is responsible for ordering the material so that it produces a diffraction pattern.
Talking across miles
We previously saw how choices made early in the tiling process can lead to patches that cannot be extended. As we will now see, this feature becomes more mysterious when the growth of quasicrystals is considered. Chemical properties of the atoms and their bonds that make up a quasicrystal are usually responsible for creating matching rules. Yet we have seen that the matching rules alone are not enough to avoid patches that cannot be further extended. How do quasicrystals make the proper choices that allow them to continue growing?
To explore this issue more deeply, let us consider an example. Suppose we begin with this patch:

and that we wish to continue laying tiles down on the sides. In particular, suppose we place a thick rhomb on the right and a thin rhomb on the left like this:

For reasons we'll understand in a moment, this patch may be indefinitely extended:

In the same way, if we place a thin rhomb on the right and a thick rhomb on the left, we may extend the patch indefinitely:


Now suppose that we place thin rhombs on both the right and left:

Beginning with this patch, we are forced to lay down the tiles shown below if the patch is to be consistent with an inflated patch.

Since no tile can be added to cover the red dot, placing the two thin rhombs on the sides of the original patch produces a patch that cannot be extended.
Let's summarize:
 |
This patch may be extended indefinitely. |
 |
This patch may be extended indefinitely. |
 |
This patch may not be extended indefinitely. |
If we want to create a tiling, we may place a thin rhomb on either side so long as there is a thick rhomb on the other side. However, we cannot place thin rhombs on both sides. That is, the presence of a thin rhomb influences which rhomb may be placed at a site far away.
The inflation hierarchy explains this fact. A little work shows that if the original patch is present, the fourth inflated tiling must contain exactly one of the lighter rhombs and exactly one of the darker rhombs.
Choosing a thick rhomb on one of the sides forces a thick rhomb to be present in the fourth inflated tiling.

Likewise, choosing a thin rhomb on one of the sides forces a thin rhomb to be present in the fourth inflated tiling.
Now if we begin with a thick rhomb on the right and a thin rhomb on the left, we find the following patch, which may be indefinitely extended, in the fourth inflated tiling.

If we begin with two thin rhombs, however, we find:

This patch in the fourth inflated tiling cannot be extended indefinitely since the red dot below cannot be covered by a tile. This implies that the original patch cannot be extended either.
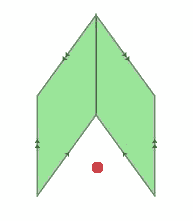
Given this understanding, it is clear that similar examples can be found in which the presence of one tile influences another site arbitrarily far away. The matching rules are local conditions; the inflation hierarchy, however, imposes global conditions that must be satisfied as well.
Of course, this poses a question about the way in which quasicrystals grow: How does the quasicrystal coordinate its growth at two sites that may be separated by a considerable distance? Several explanations have been offered. For example, Joshua Socolar has described an algorithm to place tiles so as to avoid this problem. Penrose, however, feels that something more mysterious is happening and argues that this phenomenon is the result of long-range quantum interactions. In either case, it seems that this issue has not been answered with complete satisfaction.
We'll have more to say about Penrose tilings and their construction in the December issue of this column.
References
General references on Penrose tilings and inflation
- N.G. de Bruijn, Updown generation of Penrose tilings, Indagationes Mathematicae, New Series 1(2), 1990, 201-19.
- M. Gardner, Extraordinary nonperiodic tiling that enriches the theory of tiles, Scientific American, January 1977, 110-121.
- B. Grünbaum and C.G. Shephard, Tilings and patterns, W.H. Freeman, New York, 1987.
- M. Senechal, Quasicrystals and geometry, Cambridge University Press, Cambridge, 1995.
- R. Penrose, Pentaplexity, Eureka 39, 1978, 16-22.
History and biography
- J.V. Field, Kepler's star polyhedra, Vistas Astronomy 23(2), 1979, 109-141.
- M. Senechal, The Mysterious Mr. Ammann, Mathematical Intelligencer 26, 2004, 10-21.
Quasicrystals
- R. Lifschitz, The rebirth of crystallography, Zeitschrift fur Kristallographie 217, 2002, 342-343.
- R. Lifschitz, Quasicrystals: A matter of definition, Foundations of Physics 33, 2003, 1703-1711.
- D. Schechtman et al, Metallic phase with long range orientational order and no translational symmetry, Physical Review Letters 53, 1984, 1951-1954.
Nonlocal properties of Penrose tilings
- R. Penrose, Tilings and quasicrystals: a nonlocal growth problem?, in Introduction to the Mathematics of Quasicrystals, edited by Marko Jaric, Academic Press, 1989, 53-80.
- J. Socolar, Growth rules for quasicrystals, in Quasicrystals: the state of the art, edited by D. DiVincenzo and P.J. Steinhardt, World Scientific Publishers, 213-38.
Penrose's patent
- S. Mirsky, The Emperor's New Toilet Paper, Scientific American, July 1997, 24.
- U.S. Patent and Trademark Office. To find Penrose's patent, search for patent 4,133,152.
David Austin
Grand Valley State University
david at merganser.math.gvsu.edu 
NOTE: Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet can be used to get additional bibliographic information and reviews of some these materials. Some of the items above can be accessed via the ACM Portal, which also provides bibliographic services.




































 If we now look at a tiling and superimpose the scaled rhombs formed by grouping half-rhombs, we see that another tiling is created.
If we now look at a tiling and superimpose the scaled rhombs formed by grouping half-rhombs, we see that another tiling is created.
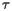 , and so the size of the tiles grows exponentially.
, and so the size of the tiles grows exponentially.










