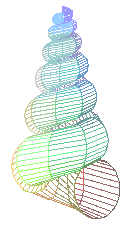The Mathematical Study of Mollusk Shells
1. Terminal growth and unchanging form
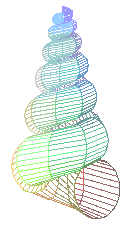 |
"But the shell retains its unchanging form in spite of itsassymetrical growth; it grows at one end only ... . And this remarkable property of increasing by terminal growth, but nevertheless retaining unchanged the form of the entire figure, is characteristic of the equiangular spiral, and of no other mathematical curve."
-Sir D'Arcy Wentworth Thompson, On Growth and Form
1942 edition,Cambridge University Press, p. 758.
|
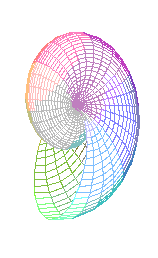 |
D'Arcy Thompson is referring to a phenomenon which everyone has observed but not everyone has pondered. The shell of a small snail is identical to the shell of a larger one of the same species, except for its size. One is an exact scale model of the other. But a snail does not enlarge its shell by uniform expansion. It adds onto it only at the open end ("terminal growth"). And it does so in such a way that the new shell is an exact scale-up of the old("unchanging form"). The combination of constraints has a mathematical consequence. Almost all mollusk shells, in all their rich variety of form, must follow the general plan of an equiangular (or, "logarithmic") spiral, or of one of its three-dimensional cousins.
The exceptions include both living and fossil species of Vermicularia and fossil ammonites of the genus Didymoceras.
In this column we will see where the equiangular spirals come into the picture, and how they can be used to generate the underlying geometry of almost every mollusk shell.
Tony Phillips
Stony Brook
Welcome to the
Feature Column!
These web essays are designed for those who have already discovered the joys of mathematics as well as for those who may be uncomfortable with mathematics.
Read more . . .
Feature Column at a glance