The Mathematical Study of Mollusk Shells

---

 

7. For further thought

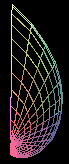
1. Bivalve shells also fit in this scheme, for example the Soft-shell Clam Mya arenaria can be modeled as follows.

v=2.5, c=3, a=0.85, b=1.6, h=0.9, k=0, t=-0.52..0.52

Experiment with modeling other bivalves, for example mussels and scallops.

2. If you live near a beach, try identifying shells and modeling them. Otherwise "Nature" stores often have inexpensive but interesting shells for sale.

3. Why is it that a helically coiled shell fits exactly inside a cone?

4. The 9 parameters we use (v, c, a, b, h, k and the beginning and end of the t range) are certainly too many.
Can 3 be enough, as in the Raup video? Think of ways to simplify the set of parameters.

5. Suppose we are down to a set of m parameters. The set of all possible parameter values is then a subset M of R^m.
Not every point of M corresponds to the coordinates of an organism. Is there some way to understand which regions of M are forbidden, and why?

6. For a fairly elementary treatment of the 3-dimensional rotation group and its subgroups you may consult the beginning of Anthony Knapp's Lie Groups, Lie Algebras, and Cohomology, Princeton University Press, 1988. This is elementary for graduate students.

The point is first to understand why the dilation equation

D_{(h1 + h2)} =D_h1 D_h2 ,        D₀ =identity

implies D_h(x,y,z) = e^vh(x,y,z). We know that since D_h is a dilation it must correspond to multiplication by some function f(h).
Since we are assuming a smooth dependence on the parameter h, we can calculate the derivative of f : f'(h)= lim_a->0 (f(h+a)-f(h))/a.
The dilation equation gives f(h+a)=f(h)f(a), so

f'(h)= lima->0 (f(h+a)-f(h))/a = lima->0 f(h)(f(a)-1)/a = v f(h), where v = lima->0(f(a)-1)/a.

The initial value problem f'(h)=v f(h),   f(0)=1 has the unique solution f(h)= e^vh.

What happens to the rotations is more complicated but completely analogous. Once we choose coordinates, R_h is a 3x3 matrix whose entries vary smoothly with h.The rotation equation is

R_{(h1 + h2)} = R_h1 R_h2 ,       R₀ = I (the identity matrix). The derivative R'_t is the matrix of the derivatives of the entries. Using the rotation equation, we have

 R't = lima->0 (R(t+a)-Rt)/a = lima->0 Rt(Ra-I)/a = Rtr, where r is the matrix lima->0(Ra-I)/a.

Now we have the matrix differential equation R'_t = R_tr ,   R₀= I.There is an exponential map exp for matrices defined by the same power series as the usual exponential. In terms of this map our equation has the unique solution R_t = exp(tr).

Finally one needs to know that the possible matrices r form a vector space spanned by

$$ \left[ \begin{array} {rrr}0 &-1 & 0\\ 1 & 0 & 0 \\ 0 &0 & 0\\ \end{array} \right] , \left[ \begin{array} {rrr}0 & 0 & -1\\ 0 & 0 & 0 \\ 1 &0 & 0\\ \end{array} \right] , \left[ \begin{array}{rrr} 0 & 0 & 0\\ 0 & 0 & -1 \\ 0 &1 & 0\\ \end{array} \right] . $$

(this is a consequence of the the R_t being matrices of rotations) and that we can choose our (x,y,z)-coordinates so that

$$ \left[ \begin{array} {ccc}0 &-c & 0\\ c & 0 & 0 \\ 0 &0 & 0\\ \end{array} \right] . $$

Then it is easy and sort of fun to check explicitly that

$$R_{t} = \exp(tr)= \left[ \begin{array} {ccc}\cos(ct) &-\sin(ct) & 0\\ \sin(ct) & \cos(ct) & 0 \\ 0 &0 & 1\\ \end{array} \right] .$$

 

---

• 1. Terminal growth and unchanging form

   

• 2. Zoning laws in Molluskville

   

• 3. Nautilus and the Ammonites

   

• 4. Things get more complicated in 3 dimensions, but Calculus comes to the rescue.

   

• 5. Mathematical models of helical shells

   

• 6. Ray Gildner's Java applet for shell sketching

   

• 7. For further thought

 

Search Feature Column