Slingshots and Space Shots
Posted May 2005.
Cassini, the spacecraft that flew through Saturn's rings not too long ago, started out from Earth with far less speed than it needed to get to its goal, and picked up what energy it needed by a succession of energy thefts.
Bill Casselman
University of British Columbia, Vancouver, Canada
cass at math.ubc.ca
Introduction
For a long time now, NASA has been using a technique that they call gravity assist and that almost all the rest of the world calls the slingshot in order to send space payloads to the far solar system using as little fuel as possible. The effects might seem miraculous to the uninitiated. Pioneer 10 was launched with enough speed to get not much further than Jupiter, but by swinging it around Jupiter it was brought to a speed sufficient to take it out of the solar system.
NASA at one of its web sites devoted to the subject says
|
The two Voyager spacecraft provide a classic example of utilizing gravity assist flybys to reach their destinations. They were launched aboard a Titan-III/Centaur, with destinations of Saturn and beyond. But their launch vehicles could provide only enough energy to get them to Jupiter (halfway out to Saturn). Had Jupiter not been present, and had the two spacecraft not encountered the giant gas planet, they would have remained in solar orbit indefinitely, farthest from the sun (known as aphelion) of Jupiter's orbital distance (5 AU or 750,000,000 km). Conversely, the spacecraft would have been closest to the sun (known as perihelion) at Earth's orbital distance (1 AU or 150,000,000 km).
The two Voyager launch times were planned so that Jupiter would coast by at just the right time. Therefore, they were influenced by Jupiter's gravitational pull and began falling toward it. Fortunately, their speeds were controlled by careful positioning of how close they came to Jupiter's orbit without impacting the planet. As the two Voyager spacecraft climbed "up" away from Jupiter, they slowed down again with respect to the gas giant, eventually reaching the same speed they had on their way in.
|
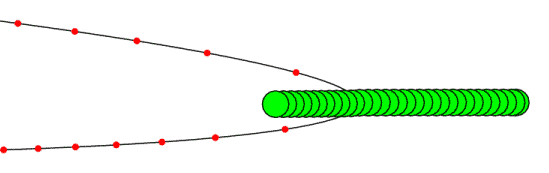
Cassini, the spacecraft that flew through Saturn's rings not too long ago, started out from Earth with far less speed than it needed to get to its goal, and picked up what energy it needed by a succession of energy thefts. Here is one of the NASA images of what the trajectory looked like:
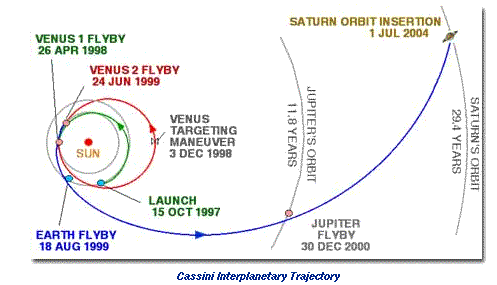
This image has been copied from NASA's site
The early techniques used were mathematically rather simple, depending essentially only on the kinematics of two isolated gravitational bodies. I'll explain this here. More recent techniques have involved a clever application of the theory of "chaos," or more prosaically the sensitive dependence of trajectories on initial conditions in the neighbourhood of an unstable equilibrium point. This is explained in a recent book by Edward Belbruno. I'll not say anything about that topic here, but hope to deal with it in a future feature.
In the last section I'll illustrate a very curious example of something like the slingshot effect that was encountered on theoretical grounds a long time before space flight.
Kepler dynamics of two isolated gravitational bodies
As a spacecraft approaches a planet, the forces on it become appreciably strong in the context where the two objects are considered, to a close approximation, as isolated from all other objects in space. Since the spacecraft comes from a great distance, it will not do too much damage to assume it comes from infinitely far away, which means that it is following a hyperbolic orbit with respect to the center of gravity of the planet and itself. I'll first recall here the situation without providing details. (Danby's book does a good job of filling them in.)
Suppose we consider more generally two objects of masses m1and m2 and positions r1 and r2. The gravitational force attracts them equally, but in opposite directions, with magnitude m1m2G/||r1 - r2||2. Writing down the vector forces and applying Newton's law, we deduce that the center of gravity moves with constant velocity. If r = r1 - r2, then a straightforward calculation gives us the differential equation
r'' = - k r /|| r ||3
where k = GM and M = m1 + m2 is the total mass. This determines how r evolves, but from the formulas
r1 = m2 r/ M
r2 = - m1 r/ M
we can track the objects themselves.
If we set h equal to the cross product r x r' of r and r', then it turns out to be constant. It is, up to mass constants, the vector representation of angular momentum. A familiar cross-product identity allows us to calculate that the vector
P = - k(r/||r||) - hx r'
is also constant. Here r/||r|| is the unit vector pointing in the same direction as r. If we choose the y-axis to point in the direction opposite to P and let (r, A) be the polar coordinates where A is the angle with respect to P, a final vector calculation gives us the equation of the trajectory in these coordinates:
r = p/(1 + e cos A)
where p = ||h||2/k, and e = ||P||/k. This is the equation of a conic section of eccentricity e and semi-latus rectum p, with origin at its focus. It is an ellipse if e < 1, a parabola if e = 1, and an hyperbola if e > 1. The division takes place according to whether the initial pair of objects has total energy negative, vanishing, or positive.
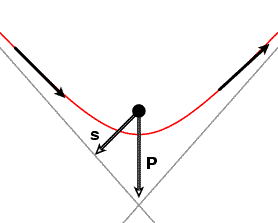
If s is the vector from the origin to the line through r in the direction of r', then h = s x r', and h x r' is -||s|| ||r'||2 times the unit vector s/||s||. We can therefore write P = ||r'||2 s - k r/||r||. The qualitative picture is this:
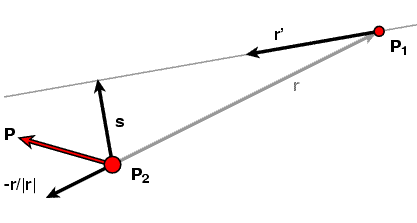
The geometry of hyperbolas
If a conic section is an ellipse, its eccentricity e measures how far it is from a circle. It will be close to 1, for example, if the ellipse is very elongated. What does the eccentricity say about the geometry of an hyperbola?
Given two points F+ and F- and a positive length 2a, the locus of all points P such that
||P - F+|| - ||P - F-|| = 2a
is an hyperbola with foci F+ and F-. If we choose coordinates so F+ = (0, d) and F-=(0, -d), then a bit of messy algebra tells us that the equation of this curve is
y2 = c2x2 + a2
where
c2 = a2/(d 2 - a2) .
Its asymptotes ("limiting" lines) are the lines y2 = c2x2, and the nearest points of the hyperbola to the origin are (0, a) and (0, -a). The polar equation r = p/(1 + e cos A) that we saw before now tells us that the direction of one of the asymptotes is Ainfinity where
cos Ainfinity = -1/e.
Therefore the eccentricity is related to the direction of the asymptotes by the equation
c2 = 1/(e2 - 1).
and comparison with an earlier formula tells us that e = d/a.

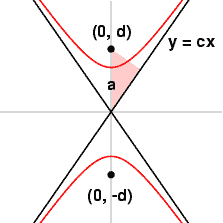
Here are a few hyperbolas with eccentricity indicated. They approach a parabola as e tends to 1.

Hyperbolic trajectories
In this section, suppose we are working with two bodies, one of them much, much larger than the other, or more precisely suppose that m1/m2 is very small. Suppose also that the larger body is not moving, or more precisely that the coordinate system is chosen at its center. Since the ratio of masses is so great, this center may be considered the center of mass of the pair, and the total mass M may be identified with m2. Finally, suppose the smaller object starts from very far away with speed v. Let s be the vector of length s from the origin to the point where it would pass by closest if gravity had no effect. As we have already seen
P/k = sv2/k - r/||r||
and since the inital velocity and position are in effect perpendicular we can calculate the eccentricity e from the formulas
e = ||P||/k
e2 = 1 + g2, where g = v2s/k
This tells us the asymptotes of the orbit, which is all that will be important. The smaller body thus swings around the origin and passes off to infinity again in a direction obtained from the original direction by rotating it through the deflection angle 2(Ainfinity-90o).

The slingshot
The paths of the objects are conic sections if the origin is taken to be their center of gravity, or more generally if the center of gravity is fixed in the coordinate system. But if the center of gravity is moving, the paths are stranger looking. For example, here is a trace of the paths if r tracks an ellipse and the center of mass is moving to the left (or maybe to the right).

If r tracks an hyperbola and the center of mass is moving, we necessarily encounter the slingshot effect. Let R be the operator that rotates a vector by the deflection angle of the orbit. In the coordinate system in which the heavy body is fixed, the final velocity is Rvi. But if the heavier body moves with velocity V it is the relative velocities that are related in this way:
vf - V = R(vi - V),
vf = Rvi + V - RV
vf = R(vi + R-1V - V)
The vector vf will have the same length as vi + V - R-1V, and will rarely have the same length as vi. The difference in lengths will amount to an acceleration or a braking action. The relationship between vi and vf is nicely illustrated by a clever diagram to be found in Bob Johnson's note.
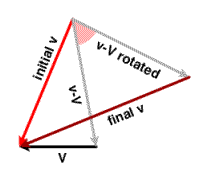

One conclusion to be drawn from the basic formula is that the acceleration or retardation will always be smaller in magnitude than 2 ||V||. The maximum acceleration will be approached only if the small object and the heavy one are moving in very close to opposite directions, and the smaller just about reverses itself. In that case the extra speed will be twice the magnitude of V.
Burrau's problem
The slingshot effect is a good example of slightly non-intuitive behaviour with a simple explanation. It is especially striking since it involves only two bodies, a configuration that is completely understood. If we start to look at the behaviour of systems of three or more objects, which is what more recent NASA techniques involve, the variety of surprises may be unlimited.
One of the earliest surprises involved a variation on the slingshot. For reasons not entirely clear to me, the astronomer Carl Burrau suggested trying to determine the motion of a system of three bodies initially at rest, of masses 3, 4, and 5 located at the vertices of a triangle of sides 3, 4, 5 with masses matching opposite sides:
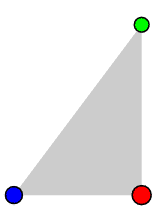
The gravitational constant is taken to be 1. Burrau himself made some attempt to chart the motion for a fairly long initial segment of time, but the long-term evolution of the system was computed successfully by Victor Szebehely and collaborators only in the mid sixties, and is remarkable:




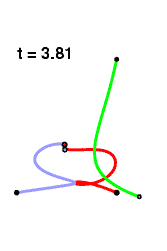
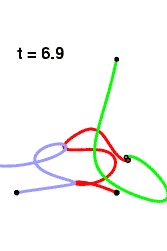



When the system starts out, it proceeds rather sedately, then gets progressively more tangled up, with the heaviest of the three bodies weaving back and forth between the lighter two. The resemblance of the traces of the motion to a plate of overcooked spaghetti is presumably accidental. Occasionally there are some very close encounters between the two heavy bodies.




But then close to t = 60 the lightest body skips off towards infinity, with the other two forming an apparently stable two body system passing off in the opposite direction!
I do not know to what extent the empirical behavior exhibited here is assured on theoretical grounds.
Remarks on programming
The diagrams above are based on those of Szebehely. They occur often in the literature. The programming underlying them is tricky, because the step size has to be reduced drastically near close encounters. I used Störmer's method with polynomial extrapolation and a primitive step adjustment procedure.
References
J. M. A. Danby, Fundamentals of celestial mechanics, Willmann-Bell, 1988.
Edward Belbruno, Capture dynamics and chaotic motions in celestial mechanics, Princeton Press, 2004.
Victor Szebehely, Burrau's problem of three bodies, P. N. A. S. 58 (1967), 60-65
A list of missions using gravity assist
A tutorial on gravity assist, by James van Allen
Johnson's home page containing a link to useful notes by Johnson
NASA's primer on gravity assists
NASA's page on Cassini and gravity assists
Bill Casselman
University of British Columbia, Vancouver, Canada
cass at math.ubc.ca
NOTE: Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet can be used to get additional bibliographic information and reviews of some these materials. Some of the items above can be accessed via the ACM Portal, which also provides bibliographic services.






























