sphericon 1 The Differential Geometry of the Sphericon
For references on polyhedral curvature see Thomas Banchoff's early research papers.
1. What is the Sphericon?
Ian Stewart's Mathematical Recreations column in the October 1999 Scientific American is entitled ``Cone with a Twist'' and describes the Sphericon, a solid invented by C. J. Roberts of Baldock, England.
The Sphericon really is a (double) cone with a twist. It is formed by taking two right-angled cones, joining them at the base, slicing the resulting solid by a plane through the two cone points, and gluing the two resulting pieces back together after having rotated one 90 degrees with respect to the other. It can be assembled out of cardboard (my favorite material is overhead transparency sheets - they are flexible but resilient and can be Xeroxed onto) by tracing and cutting out the following diagram. Then attach one green side to the other. This will bring the curved edges together two by two, where they can be zipped together with tape.
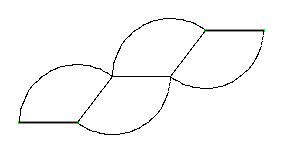
Trace an enlarged version of this diagram onto stiff plastic or paper, cut out and assemble by taping together the straight edges (highlighted in green) and then taping the curved edges together. This image was made following directions in Ian Stewart's column. The pie-slices have angle 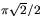 or approximately 127.3 degrees. or approximately 127.3 degrees. |
In this column we will look at this surface as a mathematical object and study its geometry. The tools for this study are the same as those used for plane geometry: measurements of lengths and angles. The difference from plane geometry is that this surface is not smooth: it has corners and creases. But we can keep track of the difference with our traditional methods.
--
Tony Phillips
SUNY at Stony Brook 


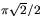 or approximately 127.3 degrees.
or approximately 127.3 degrees.